北师大版八年级数学下册课件:3.1图形的平移(共24张PPT)
文档属性
| 名称 | 北师大版八年级数学下册课件:3.1图形的平移(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 00:00:00 | ||
图片预览








文档简介
各位 同仁:
(一)感受生活,引入新课
第三章 图形的平移与旋转
这些物体的运动过程是否有共同点?
想一想
义务教育课程标准北师大版数学八年级下册第三章
3.1图形的平移(一)
知识与技能
1、通过具体实例认识平移,理解平移的基本内涵。2、理解平移前后两个图形对应点连线和对应线段分别平行(或在一条直线上)且相等,对应角相等的性质。
通过探究归纳平移的定义,特征,性质,积累数学活动经验,提高学生的科学思维能力.
能力目标
1、通过收集自己身边“平移”的实例,感受“生活处处有数学”,激发学生学习数学的兴趣。
2、通过对图形平移性质的探究,培养了学生的探索精神和合作意识。
3、通过运用图形平移的性质,增强学生的应用意识。
情感态度与价值观
教学目标
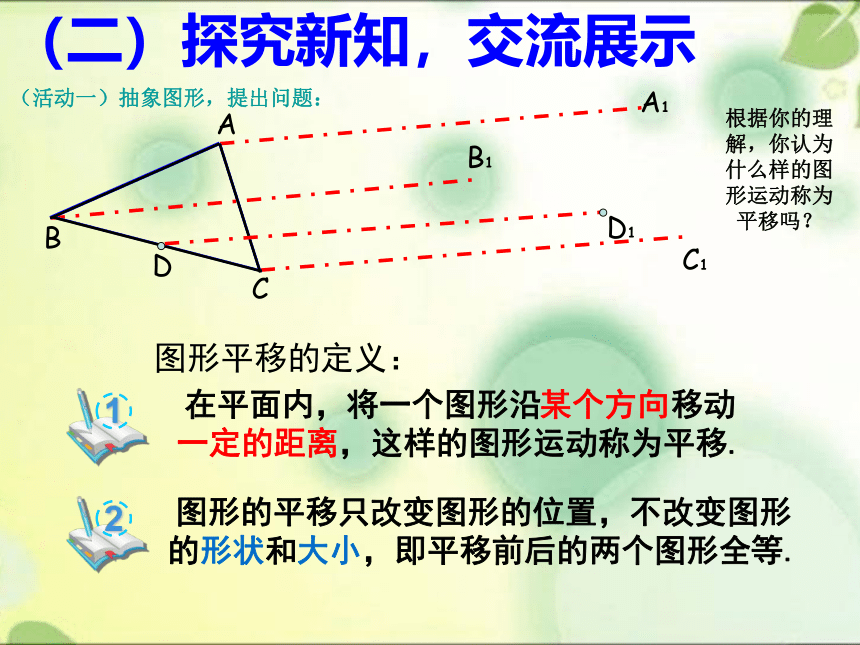
A
C
B
A1
B1
C1
D
D1
(二)探究新知,交流展示
(活动一)抽象图形,提出问题:
根据你的理解,你认为什么样的图形运动称为平移吗?
图形平移的定义:
在平面内,将一个图形沿 移动一定的距离,这样的图形运动称为平移.
某个方向
图形的平移只改变图形的位置,不改变图形的形状和大小,即平移前后的两个图形全等.
1
2
说说你生活中见过的图形的平移例子
1、下列现象中,属于平移的是:
(1)火车在笔直的铁轨上行驶
(2)冷水受热过程中小气泡上升变成大 气泡
(3)人随电梯上升
(4)钟摆的摆动
(5)飞机起飞前在直线跑道上滑动
√
√
√
(活动二)比一比,谁最棒(口答)
2、判断下面几组图形运动是不是平移?
A
C
D
B
×
×
√
×
至此我们顺利完成本节课的第一个教学目标
A
C
B
点A与点A1 叫做对应点,
A1
B1
C1
D
D1
线段AB与线段A1B1 叫做对应线段。
∠A与∠A1 叫做对应角
你还能从图中找出其他的对应点、对应线段和对应角吗?
(3)在图中,线段AA1、BB1、CC1、DD1有怎样的位置关系?
(1)?在图中任意选一组对应线段,这两条线段之间有怎样的关系??
(4)?由(1)、(2)两个问题,你能归纳出什么结论?
(2)?在图中任意选一组对应角,这两个角之间有怎样的关系??
(活动三)类比联想,归纳性质
A
B
D
C
F
G
H
E
你能否观察发现平移的性质?
探索发现
经过平移,对应点所连的线段,对应线段,对应角之间有怎样的关系?
经过平移,对应点所连的线段平行(或在一条直线上)且相等;对应线段平行(或在一条直线上)且相等,对应角相等。
1、经过平移,△ABC的顶点A移到了点D(如图所示),试画出平移后的三角形。
A
B
C
D
F
E
步骤:
1、定方向,定距离:连接 AD;
2、利用平移的性质找到B、C的对应点E、F;
3、分别连接DE、DF、EF。
作图步骤:
(1)找出关键点。
(2)作出这些点经平移后的点。
(3)将所作的对应点按原来方式连结,所得图形即是。
作点的平移的像是图形平移作图的基本方法.
“以局部带整体”的作图思想.
(三)自学质疑,学以致用
你还有画△DEF的其他办法吗?与同伴交流
B
C
A
新课讲解:平移作图
4
想一想,有其他的方法吗?
E
F
D
解:如图,过点D按射线AB的方向做线段DE平行且等于AB;过点D按射线AC的方向做线段DF平行且等于AC;连接EF. ΔDEF 就是ΔABC平移后的图形.
2.某公园计划在一块长方形草坪上修两条人行横道,修建方案如图所示,其中一条为长方形,另一条是平行四边形,求剩余草坪的面积。
4cm
7cm
2cm
1cm
(7 – 2)(4 – 1)=15m2
3.如图,在一块长为20m,宽为8m的长方形的草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是0.5m)。请你猜想草地的面积是多少。
你知道如何解答了吗?
(20 – 0.5) ×8=156m2
到此为止完成了我们的第二个教学目标
本节课你收获到了什么?
1、平移的定义:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。
2、平移不改变图形的形状和大小。
(四)感悟收获,回扣目标
3、平移的性质:经过平移,对应点所连的线段平行(或在一条直线上)且相等;对应线段平行(或在一条直线上)且相等,对应角相等。
2、经过平移,图形上每个点都沿同一个方向移动了一段
距离,下面说法正确的是 ( )
A 不同的点移动的距离不同
B 既可能相同也可能不同
C 不同的点移动的距离相同
D 无法确定
1、平移改变的是图形的 ( )
A 位置 B 大小 C 形状 D 位置、大小和形状
A
C
(五)当堂检测,巩固提高
4.如图,将线段AB向右平移得到线段CD,
如果AB=5cm,则 CD=____ cm,AC____BD.
A
B
C
D
从位置上看,AB______CD.
5
=
//
3.“小小竹排水中游,巍巍青山两岸走”,所蕴涵的图形变换是__________变换?
平移
5. △ABC是等腰直角三角形,腰长为8cm,将△ABC向下平移后,得到的△MNP是________ 三角形,它的面积______cm2
M
N
P
A
B
C
△ABC移动的距离可以用线段
________________表示
等腰直角
32
AM(或BN或CP)
6.如图,△ABC平移后得到△DEF,若∠A=26°,
∠E=74°,那么∠2=_____,∠F=_____,
∠C=_____。
74°
80°
80°
7、如图,在一个高为6m,长为10m的楼梯表面铺地毯,则地毯长度至少是( )
6m
10m
14m
谢谢,
欢迎大家批评指正!
(一)感受生活,引入新课
第三章 图形的平移与旋转
这些物体的运动过程是否有共同点?
想一想
义务教育课程标准北师大版数学八年级下册第三章
3.1图形的平移(一)
知识与技能
1、通过具体实例认识平移,理解平移的基本内涵。2、理解平移前后两个图形对应点连线和对应线段分别平行(或在一条直线上)且相等,对应角相等的性质。
通过探究归纳平移的定义,特征,性质,积累数学活动经验,提高学生的科学思维能力.
能力目标
1、通过收集自己身边“平移”的实例,感受“生活处处有数学”,激发学生学习数学的兴趣。
2、通过对图形平移性质的探究,培养了学生的探索精神和合作意识。
3、通过运用图形平移的性质,增强学生的应用意识。
情感态度与价值观
教学目标
A
C
B
A1
B1
C1
D
D1
(二)探究新知,交流展示
(活动一)抽象图形,提出问题:
根据你的理解,你认为什么样的图形运动称为平移吗?
图形平移的定义:
在平面内,将一个图形沿 移动一定的距离,这样的图形运动称为平移.
某个方向
图形的平移只改变图形的位置,不改变图形的形状和大小,即平移前后的两个图形全等.
1
2
说说你生活中见过的图形的平移例子
1、下列现象中,属于平移的是:
(1)火车在笔直的铁轨上行驶
(2)冷水受热过程中小气泡上升变成大 气泡
(3)人随电梯上升
(4)钟摆的摆动
(5)飞机起飞前在直线跑道上滑动
√
√
√
(活动二)比一比,谁最棒(口答)
2、判断下面几组图形运动是不是平移?
A
C
D
B
×
×
√
×
至此我们顺利完成本节课的第一个教学目标
A
C
B
点A与点A1 叫做对应点,
A1
B1
C1
D
D1
线段AB与线段A1B1 叫做对应线段。
∠A与∠A1 叫做对应角
你还能从图中找出其他的对应点、对应线段和对应角吗?
(3)在图中,线段AA1、BB1、CC1、DD1有怎样的位置关系?
(1)?在图中任意选一组对应线段,这两条线段之间有怎样的关系??
(4)?由(1)、(2)两个问题,你能归纳出什么结论?
(2)?在图中任意选一组对应角,这两个角之间有怎样的关系??
(活动三)类比联想,归纳性质
A
B
D
C
F
G
H
E
你能否观察发现平移的性质?
探索发现
经过平移,对应点所连的线段,对应线段,对应角之间有怎样的关系?
经过平移,对应点所连的线段平行(或在一条直线上)且相等;对应线段平行(或在一条直线上)且相等,对应角相等。
1、经过平移,△ABC的顶点A移到了点D(如图所示),试画出平移后的三角形。
A
B
C
D
F
E
步骤:
1、定方向,定距离:连接 AD;
2、利用平移的性质找到B、C的对应点E、F;
3、分别连接DE、DF、EF。
作图步骤:
(1)找出关键点。
(2)作出这些点经平移后的点。
(3)将所作的对应点按原来方式连结,所得图形即是。
作点的平移的像是图形平移作图的基本方法.
“以局部带整体”的作图思想.
(三)自学质疑,学以致用
你还有画△DEF的其他办法吗?与同伴交流
B
C
A
新课讲解:平移作图
4
想一想,有其他的方法吗?
E
F
D
解:如图,过点D按射线AB的方向做线段DE平行且等于AB;过点D按射线AC的方向做线段DF平行且等于AC;连接EF. ΔDEF 就是ΔABC平移后的图形.
2.某公园计划在一块长方形草坪上修两条人行横道,修建方案如图所示,其中一条为长方形,另一条是平行四边形,求剩余草坪的面积。
4cm
7cm
2cm
1cm
(7 – 2)(4 – 1)=15m2
3.如图,在一块长为20m,宽为8m的长方形的草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是0.5m)。请你猜想草地的面积是多少。
你知道如何解答了吗?
(20 – 0.5) ×8=156m2
到此为止完成了我们的第二个教学目标
本节课你收获到了什么?
1、平移的定义:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。
2、平移不改变图形的形状和大小。
(四)感悟收获,回扣目标
3、平移的性质:经过平移,对应点所连的线段平行(或在一条直线上)且相等;对应线段平行(或在一条直线上)且相等,对应角相等。
2、经过平移,图形上每个点都沿同一个方向移动了一段
距离,下面说法正确的是 ( )
A 不同的点移动的距离不同
B 既可能相同也可能不同
C 不同的点移动的距离相同
D 无法确定
1、平移改变的是图形的 ( )
A 位置 B 大小 C 形状 D 位置、大小和形状
A
C
(五)当堂检测,巩固提高
4.如图,将线段AB向右平移得到线段CD,
如果AB=5cm,则 CD=____ cm,AC____BD.
A
B
C
D
从位置上看,AB______CD.
5
=
//
3.“小小竹排水中游,巍巍青山两岸走”,所蕴涵的图形变换是__________变换?
平移
5. △ABC是等腰直角三角形,腰长为8cm,将△ABC向下平移后,得到的△MNP是________ 三角形,它的面积______cm2
M
N
P
A
B
C
△ABC移动的距离可以用线段
________________表示
等腰直角
32
AM(或BN或CP)
6.如图,△ABC平移后得到△DEF,若∠A=26°,
∠E=74°,那么∠2=_____,∠F=_____,
∠C=_____。
74°
80°
80°
7、如图,在一个高为6m,长为10m的楼梯表面铺地毯,则地毯长度至少是( )
6m
10m
14m
谢谢,
欢迎大家批评指正!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
