北师大版八年级下册1.1等腰三角形 课件 (共27张PPT)
文档属性
| 名称 | 北师大版八年级下册1.1等腰三角形 课件 (共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 00:00:00 | ||
图片预览





文档简介
学习
目标
1.等腰三角形及其相关概念
。
2.等腰三角形的性质
。
3.等腰三角形的概念及性质的应用
。
3.等腰三角形一腰上的高与另一腰的夹角为60°,则这个等腰三角形的顶角为(
)
A.30°
B.150°
C.30°或150°
D.120°
预习
探路
1.△ABC中,AB=AC,∠A=70°,则∠B=______
2.等腰三角形一底角的外角为105°,那么它的顶角为______度
C
55°
30
创设情境
创设情境
下载图片
创设情境
等腰三角形
你知道什么是等腰三角形吗?
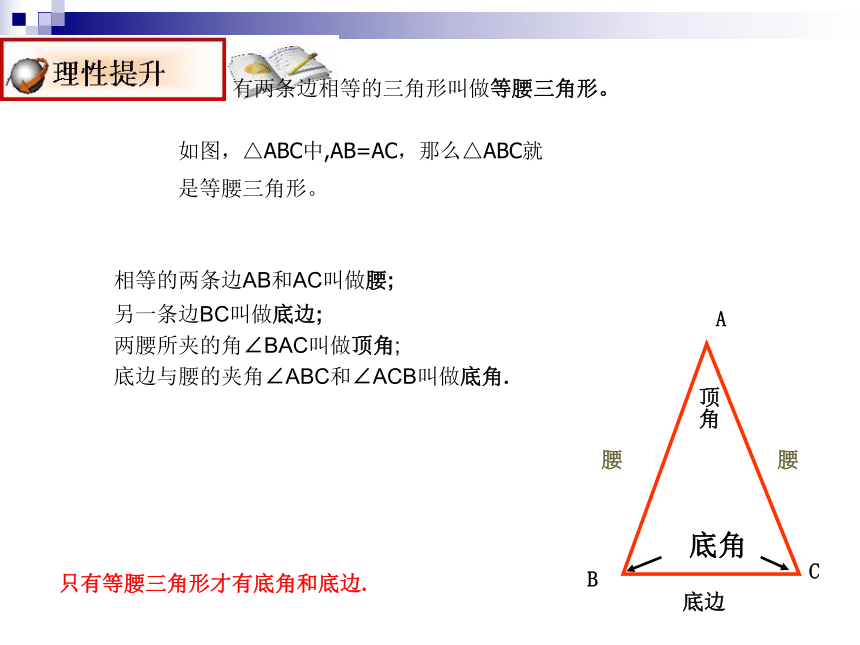
有两条边相等的三角形叫做等腰三角形。
A
B
C
腰
腰
底边
底角
顶角
相等的两条边AB和AC叫做腰;
另一条边BC叫做底边;
两腰所夹的角∠BAC叫做顶角;
底边与腰的夹角∠ABC和∠ACB叫做底角.
如图,△ABC中,AB=AC,那么△ABC就
是等腰三角形。
只有等腰三角形才有底角和底边.
A
B
C
D
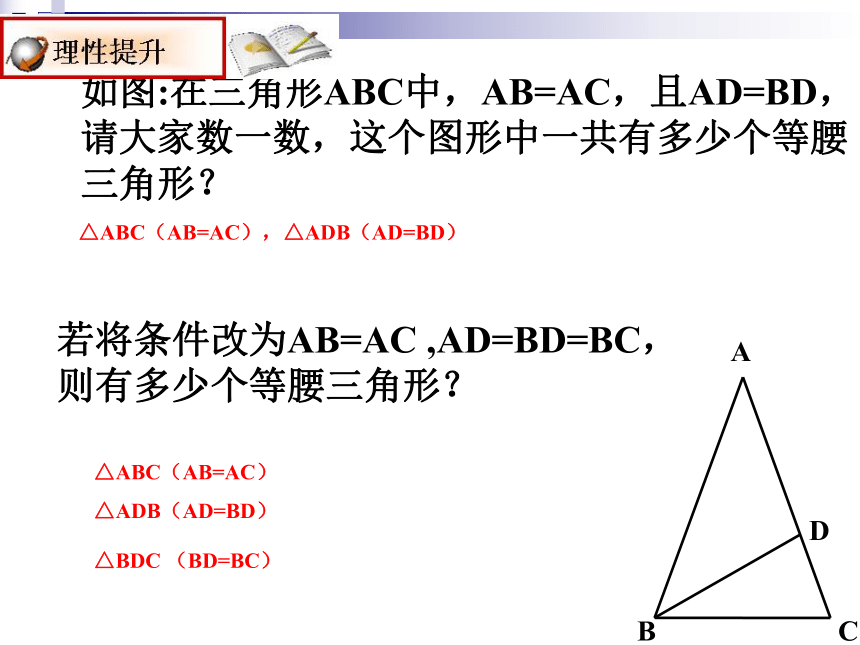
如图:在三角形ABC中,AB=AC,且AD=BD,请大家数一数,这个图形中一共有多少个等腰三角形?
△ABC(AB=AC),△ADB(AD=BD)
若将条件改为AB=AC
,AD=BD=BC,则有多少个等腰三角形?
△ABC(AB=AC)
△ADB(AD=BD)
△BDC
(BD=BC)
材料:
剪刀、一张矩形纸
方法:(1)先将矩形纸按图中虚线对折;
(2)剪去阴影部分;
(3)将剩余部分展开。
大胆猜测
请同学们拿出你们刚剪好的等腰三角形
纸片,它除了两腰相等以外,你还能发
现什么?
A
B
C
如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,我们就说这个图形关于这条直线对称,那么这个图形就叫轴对称图形,这条直线叫对称轴.互相重合的点是对应点,叫做对称点.
返回
设问:你发现了什么现象,
猜想等腰△ABC有哪些性质?
角:
①
∠B
=
∠C
②
∠BAD=∠CDA
③∠ADC=
∠ADB=900
边:
④BD
=
CD
→
两个底角相等
→
AD为顶角∠BAC的平分线
→
AD为底边BC上的高
→
AD为底边BC上的中线
结论:
等腰三角形是轴对称图形;
等腰三角形性质
性质1
等腰三角形的两个底角相等(简写成“等边对等角”);
性质2
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。(可简记为“三线合一”)
证明:
作顶角的平分线AD.
在△BAD和△CAD中,
AB=AC
(
已知
),
∠
1=
∠
2
(
辅助线作法
),
AD=AD
(公共边)
,
∴
△BAD
≌
△CAD
(SAS).
∴
∠
B=
∠C
(全等三角形的对应角相等).
已知:
△
ABC中,AB=AC.
求证:
∠B=
∠C.
A
B
C
1
2
证明:等腰三角形的两个底角相等
作顶角的平分线
D
证明:
作底边中线AD.
在△BAD和△CAD中,
AB=AC
(
已知
),
BD=CD
(
辅助线作法
),
AD=AD
(公共边)
,
∴
△BAD
≌
△CAD
(SSS).
∴
∠
B=
∠C
(全等三角形的对应角相等).
已知:
△
ABC中,AB=AC.
求证:
∠B=
∠C.
A
B
C
D
证明:等腰三角形的两个底角相等
作底边中线
证明:
作底边高线AD.
AB=AC
(
已知
),
AD=AD
(公共边)
,
∴
Rt
△BAD
≌
Rt
△CAD
(HL).
∴
∠
B=
∠C
(全等三角形的对应角相等).
已知:
△
ABC中,AB=AC.
求证:
∠B=
∠C.
A
B
C
D
证明:等腰三角形的两个底角相等
作底边的高线
在Rt△BAD和△RtCAD中,
等腰三角形的性质
1
等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
例1
在三角形ABC中,已知AB=AC,且∠B=80°
,则∠C=
___度,∠A=____度?
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
∵∠B=80°
(已知)
∴∠C=80°
又∵∠A+∠B+∠C=180°
(三角形内角和为180°
)
∴∠A=180°-
∠B-∠C
∠A=20°
B
C
A
等腰三角形的性质
1
等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
操练1
在三角形ABC中,已知AB=AC,且∠
A=50°
,则∠B=——度,∠C=——度?
C
B
A
∵AB=AC(已知)
∴∠B=∠C(等边对等角)又∵∠A+∠B+∠C=180°
(三角形内角和为180°
)
∠A=50°
(已知)
∴∠B=65°
∠C=65°
小结归纳
1
等腰三角形的性质定理
等腰三角形的两个底角相等
(简写成“等边对等角”)
等腰三角形顶角的平分线平分底边并且垂直于底边.
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.
“三线合一”
随堂练习
1.判断下列语句是否正确。
(1)等腰三角形的角平分线、中线和高互相重合。(
)
(2)有一个角是60°的等腰三角形,其它两个
内角也为60°.
(
)
(3)等腰三角形的底角都是锐角.
(
)
(4)钝角三角形不可能是等腰三角形
.
(
)
×
×
随堂练习
2.
在三角形ABC中,AB=AC,且AD
⊥BC,已知BD=2cm,求DC=___cm,
BC=___cm?
C
B
D
A
1
2
∵
AB=AC
,AD
⊥BC(已知)
∴BD=CD(等腰三角形的高与底边上的中线重合)
即(等腰三角形三线合一)
∵BD=2cm(已知)
∴CD=2cm
随堂练习
3.已知AD⊥
BC,试找出等腰三角形ABC
(AB=AC)中,存在相等关系的量。
C
B
D
A
1
2
∠B=∠C
∠1=∠2
∠BDA=∠CDA=90°
BD=CD
1.(2010.江西)已知等腰三角形的两条边长分别是7和3,则下列四个数中,第三条边的长是(
)
A.
8
B.
7
C.
4
D.
3.
中考链接
1
2.
(2010.宁波)
如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是△ABC、△BCD的角平分线,
则图中的等腰三角形有(
)
A.5个
B.4个
C.3个
D.2个
A
B
当堂测试
⒈等腰三角形一个底角为70°,它的顶角为______.
⒉等腰三角形一个角为70°,它的另外两个角为
__________________.
⒊等腰三角形一个角为110°,它的另外两个角为_______.
①
顶角+2×底角=180°
②
顶角=180°-2×底角
③
底角=(180°-顶角)÷2
④0°<顶角<180°
⑤0°<底角<90°
结论:在等腰三角形中,
40
°
35
°,35
°
70°,40°或55°,55°
4.
根据等腰三角形的性质,在△ABC中,
AB=AC时,
(1)
∵AD⊥BC,∴∠_____
=
∠_____,____=
____.
(2)
∵AD是中线,∴____⊥____
,∠_____
=∠_____.
(3)
∵AD是角平分线,∴____
⊥____
,_____
=_____.
A
B
C
D
BAD
CAD
CAD
BD
CD
AD
BC
BD
BAD
BC
AD
CD
当堂测试
5.
如图,在等腰三角形ABC中,AB=AC,D为BC的中点,则点D到AB,AC的距离相等。请说明理由。
┐
┐
A
E
F
B
D
C
当堂测试
解:相等,理由如下:
连接AD
在△ABC中,
∵AB=AC,D为BC中点
∴AD平分∠BAC
∵DE⊥AB,DF⊥AC
∴DE=DF
小结归纳
2
通过本节课的学习,你有哪些收获?
性质1:等边对等角
性质2:“三线合一”
常用来证明两角相等,求等腰三角形各角的度数.
研究等腰三角形的有关问题时“三线”是常用的辅助线.
等
腰
三
角
形
目标
1.等腰三角形及其相关概念
。
2.等腰三角形的性质
。
3.等腰三角形的概念及性质的应用
。
3.等腰三角形一腰上的高与另一腰的夹角为60°,则这个等腰三角形的顶角为(
)
A.30°
B.150°
C.30°或150°
D.120°
预习
探路
1.△ABC中,AB=AC,∠A=70°,则∠B=______
2.等腰三角形一底角的外角为105°,那么它的顶角为______度
C
55°
30
创设情境
创设情境
下载图片
创设情境
等腰三角形
你知道什么是等腰三角形吗?
有两条边相等的三角形叫做等腰三角形。
A
B
C
腰
腰
底边
底角
顶角
相等的两条边AB和AC叫做腰;
另一条边BC叫做底边;
两腰所夹的角∠BAC叫做顶角;
底边与腰的夹角∠ABC和∠ACB叫做底角.
如图,△ABC中,AB=AC,那么△ABC就
是等腰三角形。
只有等腰三角形才有底角和底边.
A
B
C
D
如图:在三角形ABC中,AB=AC,且AD=BD,请大家数一数,这个图形中一共有多少个等腰三角形?
△ABC(AB=AC),△ADB(AD=BD)
若将条件改为AB=AC
,AD=BD=BC,则有多少个等腰三角形?
△ABC(AB=AC)
△ADB(AD=BD)
△BDC
(BD=BC)
材料:
剪刀、一张矩形纸
方法:(1)先将矩形纸按图中虚线对折;
(2)剪去阴影部分;
(3)将剩余部分展开。
大胆猜测
请同学们拿出你们刚剪好的等腰三角形
纸片,它除了两腰相等以外,你还能发
现什么?
A
B
C
如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,我们就说这个图形关于这条直线对称,那么这个图形就叫轴对称图形,这条直线叫对称轴.互相重合的点是对应点,叫做对称点.
返回
设问:你发现了什么现象,
猜想等腰△ABC有哪些性质?
角:
①
∠B
=
∠C
②
∠BAD=∠CDA
③∠ADC=
∠ADB=900
边:
④BD
=
CD
→
两个底角相等
→
AD为顶角∠BAC的平分线
→
AD为底边BC上的高
→
AD为底边BC上的中线
结论:
等腰三角形是轴对称图形;
等腰三角形性质
性质1
等腰三角形的两个底角相等(简写成“等边对等角”);
性质2
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。(可简记为“三线合一”)
证明:
作顶角的平分线AD.
在△BAD和△CAD中,
AB=AC
(
已知
),
∠
1=
∠
2
(
辅助线作法
),
AD=AD
(公共边)
,
∴
△BAD
≌
△CAD
(SAS).
∴
∠
B=
∠C
(全等三角形的对应角相等).
已知:
△
ABC中,AB=AC.
求证:
∠B=
∠C.
A
B
C
1
2
证明:等腰三角形的两个底角相等
作顶角的平分线
D
证明:
作底边中线AD.
在△BAD和△CAD中,
AB=AC
(
已知
),
BD=CD
(
辅助线作法
),
AD=AD
(公共边)
,
∴
△BAD
≌
△CAD
(SSS).
∴
∠
B=
∠C
(全等三角形的对应角相等).
已知:
△
ABC中,AB=AC.
求证:
∠B=
∠C.
A
B
C
D
证明:等腰三角形的两个底角相等
作底边中线
证明:
作底边高线AD.
AB=AC
(
已知
),
AD=AD
(公共边)
,
∴
Rt
△BAD
≌
Rt
△CAD
(HL).
∴
∠
B=
∠C
(全等三角形的对应角相等).
已知:
△
ABC中,AB=AC.
求证:
∠B=
∠C.
A
B
C
D
证明:等腰三角形的两个底角相等
作底边的高线
在Rt△BAD和△RtCAD中,
等腰三角形的性质
1
等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
例1
在三角形ABC中,已知AB=AC,且∠B=80°
,则∠C=
___度,∠A=____度?
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
∵∠B=80°
(已知)
∴∠C=80°
又∵∠A+∠B+∠C=180°
(三角形内角和为180°
)
∴∠A=180°-
∠B-∠C
∠A=20°
B
C
A
等腰三角形的性质
1
等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
操练1
在三角形ABC中,已知AB=AC,且∠
A=50°
,则∠B=——度,∠C=——度?
C
B
A
∵AB=AC(已知)
∴∠B=∠C(等边对等角)又∵∠A+∠B+∠C=180°
(三角形内角和为180°
)
∠A=50°
(已知)
∴∠B=65°
∠C=65°
小结归纳
1
等腰三角形的性质定理
等腰三角形的两个底角相等
(简写成“等边对等角”)
等腰三角形顶角的平分线平分底边并且垂直于底边.
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.
“三线合一”
随堂练习
1.判断下列语句是否正确。
(1)等腰三角形的角平分线、中线和高互相重合。(
)
(2)有一个角是60°的等腰三角形,其它两个
内角也为60°.
(
)
(3)等腰三角形的底角都是锐角.
(
)
(4)钝角三角形不可能是等腰三角形
.
(
)
×
×
随堂练习
2.
在三角形ABC中,AB=AC,且AD
⊥BC,已知BD=2cm,求DC=___cm,
BC=___cm?
C
B
D
A
1
2
∵
AB=AC
,AD
⊥BC(已知)
∴BD=CD(等腰三角形的高与底边上的中线重合)
即(等腰三角形三线合一)
∵BD=2cm(已知)
∴CD=2cm
随堂练习
3.已知AD⊥
BC,试找出等腰三角形ABC
(AB=AC)中,存在相等关系的量。
C
B
D
A
1
2
∠B=∠C
∠1=∠2
∠BDA=∠CDA=90°
BD=CD
1.(2010.江西)已知等腰三角形的两条边长分别是7和3,则下列四个数中,第三条边的长是(
)
A.
8
B.
7
C.
4
D.
3.
中考链接
1
2.
(2010.宁波)
如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是△ABC、△BCD的角平分线,
则图中的等腰三角形有(
)
A.5个
B.4个
C.3个
D.2个
A
B
当堂测试
⒈等腰三角形一个底角为70°,它的顶角为______.
⒉等腰三角形一个角为70°,它的另外两个角为
__________________.
⒊等腰三角形一个角为110°,它的另外两个角为_______.
①
顶角+2×底角=180°
②
顶角=180°-2×底角
③
底角=(180°-顶角)÷2
④0°<顶角<180°
⑤0°<底角<90°
结论:在等腰三角形中,
40
°
35
°,35
°
70°,40°或55°,55°
4.
根据等腰三角形的性质,在△ABC中,
AB=AC时,
(1)
∵AD⊥BC,∴∠_____
=
∠_____,____=
____.
(2)
∵AD是中线,∴____⊥____
,∠_____
=∠_____.
(3)
∵AD是角平分线,∴____
⊥____
,_____
=_____.
A
B
C
D
BAD
CAD
CAD
BD
CD
AD
BC
BD
BAD
BC
AD
CD
当堂测试
5.
如图,在等腰三角形ABC中,AB=AC,D为BC的中点,则点D到AB,AC的距离相等。请说明理由。
┐
┐
A
E
F
B
D
C
当堂测试
解:相等,理由如下:
连接AD
在△ABC中,
∵AB=AC,D为BC中点
∴AD平分∠BAC
∵DE⊥AB,DF⊥AC
∴DE=DF
小结归纳
2
通过本节课的学习,你有哪些收获?
性质1:等边对等角
性质2:“三线合一”
常用来证明两角相等,求等腰三角形各角的度数.
研究等腰三角形的有关问题时“三线”是常用的辅助线.
等
腰
三
角
形
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
