北师大版八年级数学下册第三章《图形的平移与旋转回顾与思考》教学课件 (共26张PPT)
文档属性
| 名称 | 北师大版八年级数学下册第三章《图形的平移与旋转回顾与思考》教学课件 (共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 134.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 11:14:16 | ||
图片预览


文档简介
回顾与思考
图形的平移与旋转
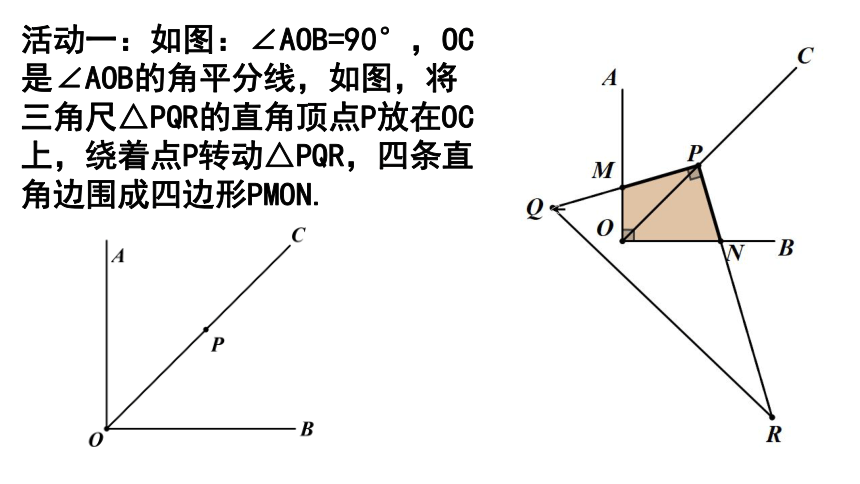
活动一:如图:∠AOB=90°,OC是∠AOB的角平分线,如图,将三角尺△PQR的直角顶点P放在OC上,绕着点P转动△PQR,四条直角边围成四边形PMON.
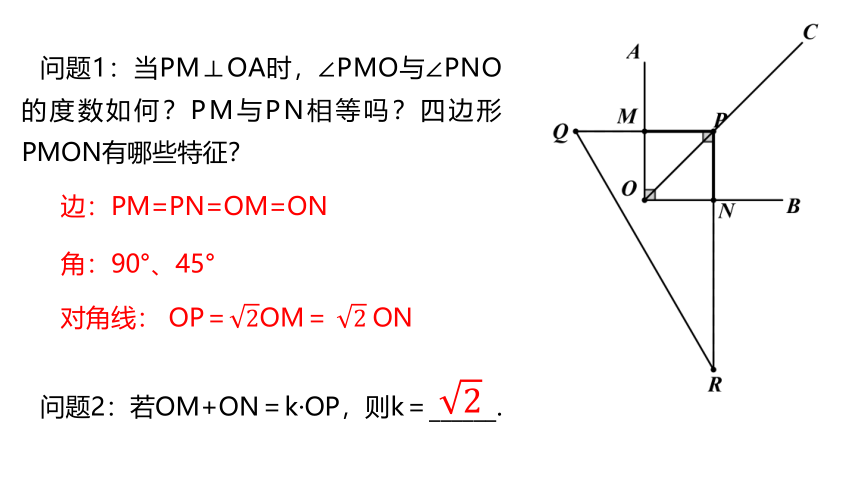
问题1:当PM⊥OA时,∠PMO与∠PNO的度数如何?PM与PN相等吗?四边形PMON有哪些特征?
问题2:若OM+ON=k·OP,则k=______.
边:PM=PN=OM=ON
对角线: OP=2OM= 2?ON
?
角:90°、45°
2
?
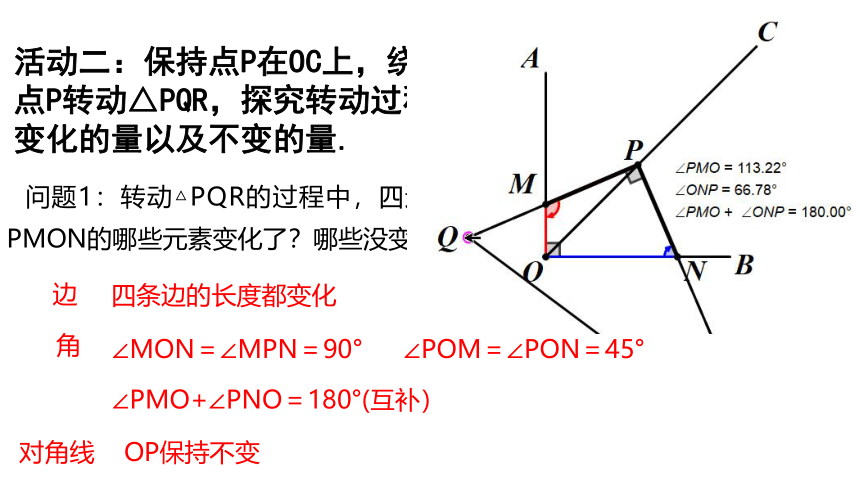
活动二:保持点P在OC上,绕着点P转动△PQR,探究转动过程中变化的量以及不变的量.
问题1:转动△PQR的过程中,四边形PMON的哪些元素变化了?哪些没变?
边
∠POM=∠PON=45°
角
∠MON=∠MPN=90°
∠PMO+∠PNO=180°(互补)
对角线
OP保持不变
四条边的长度都变化
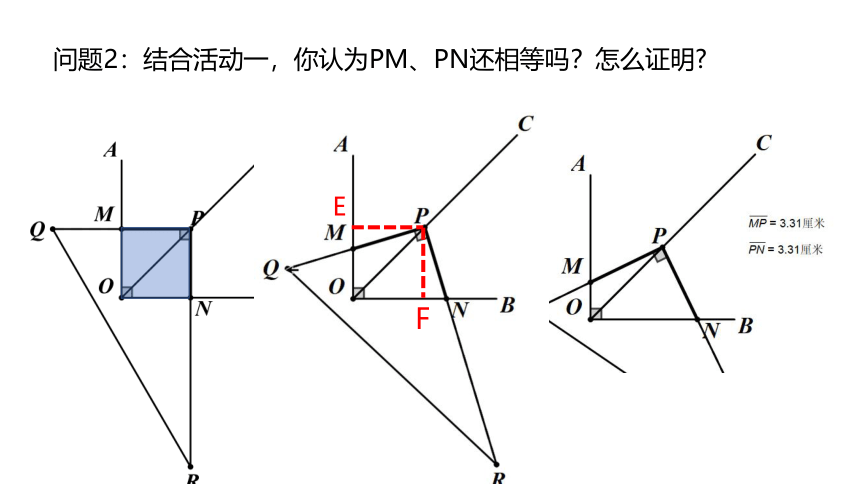
问题2:结合活动一,你认为PM、PN还相等吗?怎么证明?
E
F
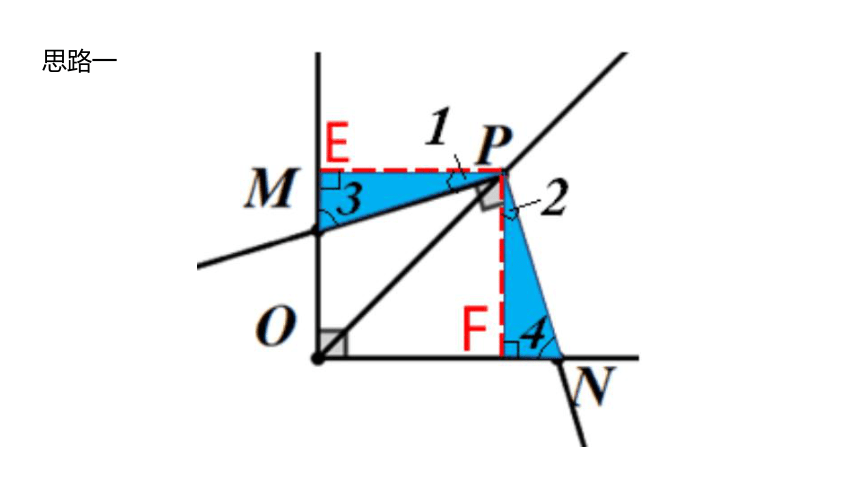
思路一
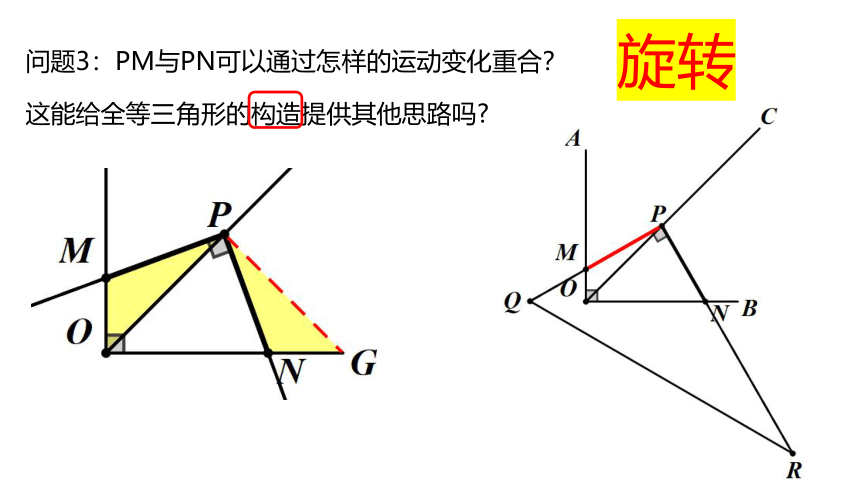
问题3:PM与PN可以通过怎样的运动变化重合?
这能给全等三角形的构造提供其他思路吗?
旋转
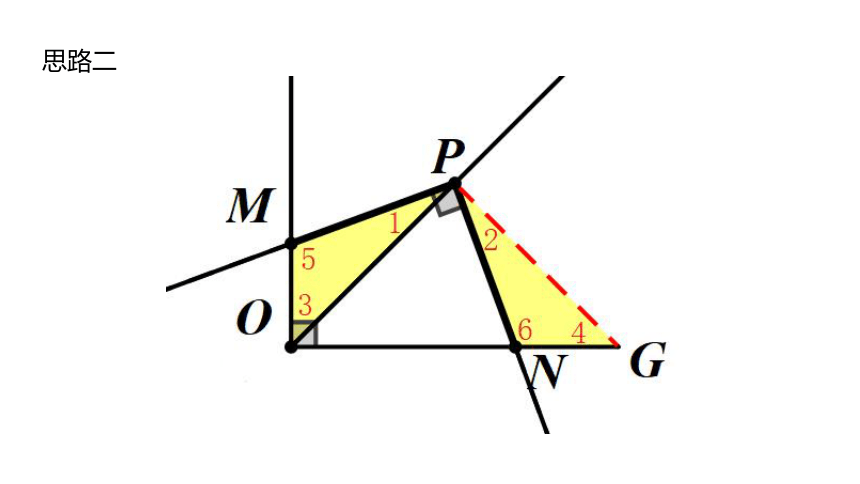
思路二
问题4:OM+ON= 2OP还成立吗?
?
OM+ON=定值
∠PMO+∠PNO=定值(180°)
OM+ON
=OM+OF+FN
=OM+OF+EM
=OE+OF
=2OP
?
OM+ON
=NG+ON
=OG
=2OP
?
四边形PMON的什么特征保证了OM在旋转后能与ON拼合在同一直线上?
∠PMO+∠PNO=180°(互补)
O、N、G三点共线
问题5:如果点M移动到了射线OA的反向延长线上,这两个结论还成立吗?
如何证明这个结论,前面证明三角形全等的思路能否用在这里?
PM=PN
思路:PM带着△POM绕点P旋转90°,
OP旋转后的位置就是辅助线的位置
ON-OM
=OG+GN-GN
=OG
=2OP
?
PM=PN
活动三:改变∠AOB的度数,探究旋转过程中的不变规律.
问题1:已知∠AOB=120°,OC是它的角平分线,利用手中的三角尺选择一个特殊的角∠QPR(如30°,45°,60°,90°,120°等),使其顶点P在OC上.使∠QPR在绕点P旋转的过程中PM=PN仍然成立,∠QPR应取多少度?
问题2:为了证明PM=PN,你按什么样的思路寻找全等三角形?
旋转
辅助线
【过点P作∠OPG=∠MPN=60° ,
交ON的延长线于点G】
【证明△POM≌△PGN】
PM=PN
OM+ON
=NG+ON
=OG
=OP
问题3:刚才的结论:OM+ON=2OP还成立吗?
?
问题4:四边形OMPN的什么特征保证了OM在旋转后能与ON共线?
∠PMO+∠PNO=180°(互补)
O、N、G三点共线
问题4: 如果∠MON=α,∠MPN=β,你认为α与β应该满足什么关系才能使PM=PN成立?如何证明?
β
?
∝2
?
180°?β?∝2=α- ∝2= ∝2
?
PM=PN
OM+ON=定值
【过点P作∠OPG=∠MPN=β ,
交ON的延长线于点G】
你能给这种最一般的情况取个名字吗?
α+β
=180°(互补)
(三)巩固应用
1.已知:在正方形ABCD中,P为直线AD上一点,连接 BP,以BP为底边作等腰直角三角形△PBE,连接AE.
(1)如图 1,当点 P 在线段AD上时,求证:AB+AP=2AE;
(2)如图 2, 当点 P 在线段 DA 的延长线上时,线段 AB、AP、AE 的数量关系是___________________.
?
AB+AP
=AB+BG
=AG
=2AE
?
AB-AP
=AB-BG
=AG
=2AE
?
G
G
(五)回顾思考
1.今天学习了什么数学模型?
2.你是如何记住这个模型的?它的最本质的特征是什么?
3.它有几种特殊情况?分别对应着什么结论?
4.在证明结论时哪一部分最重要?你的思路是什么?
5.在证明三角形全等时哪一部分最困难?你的方法是什么?
6.你在学习过程中有哪些新的体验?感受到了哪些思想方法?
祝你成功
图形的平移与旋转
活动一:如图:∠AOB=90°,OC是∠AOB的角平分线,如图,将三角尺△PQR的直角顶点P放在OC上,绕着点P转动△PQR,四条直角边围成四边形PMON.
问题1:当PM⊥OA时,∠PMO与∠PNO的度数如何?PM与PN相等吗?四边形PMON有哪些特征?
问题2:若OM+ON=k·OP,则k=______.
边:PM=PN=OM=ON
对角线: OP=2OM= 2?ON
?
角:90°、45°
2
?
活动二:保持点P在OC上,绕着点P转动△PQR,探究转动过程中变化的量以及不变的量.
问题1:转动△PQR的过程中,四边形PMON的哪些元素变化了?哪些没变?
边
∠POM=∠PON=45°
角
∠MON=∠MPN=90°
∠PMO+∠PNO=180°(互补)
对角线
OP保持不变
四条边的长度都变化
问题2:结合活动一,你认为PM、PN还相等吗?怎么证明?
E
F
思路一
问题3:PM与PN可以通过怎样的运动变化重合?
这能给全等三角形的构造提供其他思路吗?
旋转
思路二
问题4:OM+ON= 2OP还成立吗?
?
OM+ON=定值
∠PMO+∠PNO=定值(180°)
OM+ON
=OM+OF+FN
=OM+OF+EM
=OE+OF
=2OP
?
OM+ON
=NG+ON
=OG
=2OP
?
四边形PMON的什么特征保证了OM在旋转后能与ON拼合在同一直线上?
∠PMO+∠PNO=180°(互补)
O、N、G三点共线
问题5:如果点M移动到了射线OA的反向延长线上,这两个结论还成立吗?
如何证明这个结论,前面证明三角形全等的思路能否用在这里?
PM=PN
思路:PM带着△POM绕点P旋转90°,
OP旋转后的位置就是辅助线的位置
ON-OM
=OG+GN-GN
=OG
=2OP
?
PM=PN
活动三:改变∠AOB的度数,探究旋转过程中的不变规律.
问题1:已知∠AOB=120°,OC是它的角平分线,利用手中的三角尺选择一个特殊的角∠QPR(如30°,45°,60°,90°,120°等),使其顶点P在OC上.使∠QPR在绕点P旋转的过程中PM=PN仍然成立,∠QPR应取多少度?
问题2:为了证明PM=PN,你按什么样的思路寻找全等三角形?
旋转
辅助线
【过点P作∠OPG=∠MPN=60° ,
交ON的延长线于点G】
【证明△POM≌△PGN】
PM=PN
OM+ON
=NG+ON
=OG
=OP
问题3:刚才的结论:OM+ON=2OP还成立吗?
?
问题4:四边形OMPN的什么特征保证了OM在旋转后能与ON共线?
∠PMO+∠PNO=180°(互补)
O、N、G三点共线
问题4: 如果∠MON=α,∠MPN=β,你认为α与β应该满足什么关系才能使PM=PN成立?如何证明?
β
?
∝2
?
180°?β?∝2=α- ∝2= ∝2
?
PM=PN
OM+ON=定值
【过点P作∠OPG=∠MPN=β ,
交ON的延长线于点G】
你能给这种最一般的情况取个名字吗?
α+β
=180°(互补)
(三)巩固应用
1.已知:在正方形ABCD中,P为直线AD上一点,连接 BP,以BP为底边作等腰直角三角形△PBE,连接AE.
(1)如图 1,当点 P 在线段AD上时,求证:AB+AP=2AE;
(2)如图 2, 当点 P 在线段 DA 的延长线上时,线段 AB、AP、AE 的数量关系是___________________.
?
AB+AP
=AB+BG
=AG
=2AE
?
AB-AP
=AB-BG
=AG
=2AE
?
G
G
(五)回顾思考
1.今天学习了什么数学模型?
2.你是如何记住这个模型的?它的最本质的特征是什么?
3.它有几种特殊情况?分别对应着什么结论?
4.在证明结论时哪一部分最重要?你的思路是什么?
5.在证明三角形全等时哪一部分最困难?你的方法是什么?
6.你在学习过程中有哪些新的体验?感受到了哪些思想方法?
祝你成功
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
