北师大版八年级下册数学《第三章 图形的平移与旋转》复习课课件 (共23张PPT)
文档属性
| 名称 | 北师大版八年级下册数学《第三章 图形的平移与旋转》复习课课件 (共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 00:00:00 | ||
图片预览





文档简介
八年级下册数学(北师大版)
复习课
第三章 图形的平移与旋转
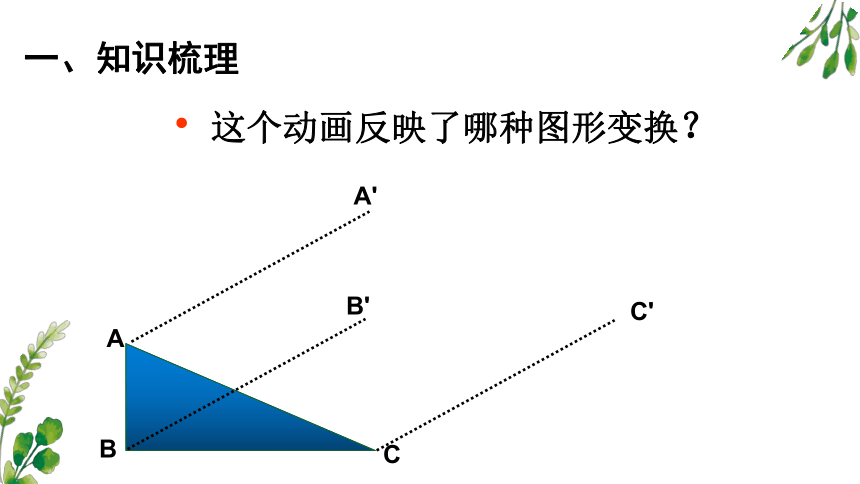
一、知识梳理
这个动画反映了哪种图形变换?
A
B
C
A'
B'
C'
一、平移:在平面内,把一个图形沿着某个方向移动一定的距离,这样的图形运动称为平移。
平移不改变图形的形状和大小。
平移的基本性质:
经过平移
对应点所连的线段平行(或在同一直线上)且相等;
对应线段平行(或在同一直线上)且相等;
对应角相等。
20
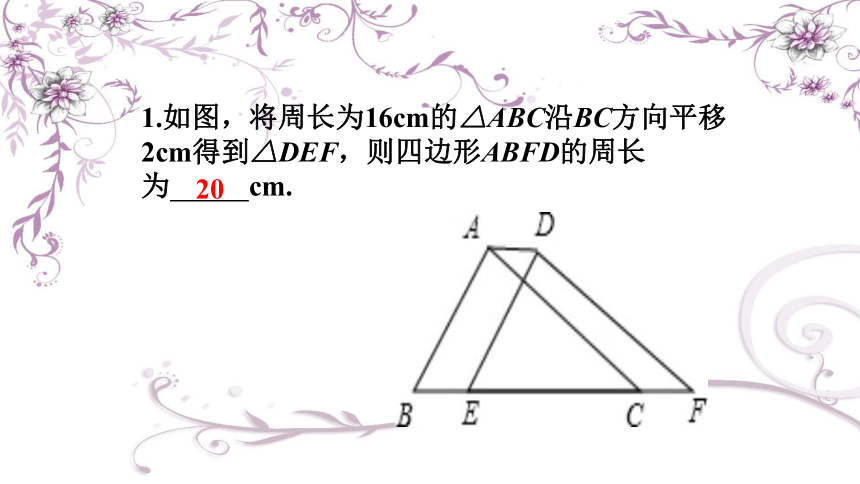
1.如图,将周长为16cm的△ABC沿BC方向平移2cm得到△DEF,则四边形ABFD的周长
为 cm.
D
这个动画反映了哪种图形变换?
二、旋转:在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。这个定点称为旋转中心,转动的角称为旋转角。
旋转不改变图形的形状和大小。
1.旋转图形的任意一组对应点与旋转中心的连线所成的角都等于旋转角。
2. 对应点到旋转中心的距离相等。
3. 旋转后的图形与原图形全等。
旋转的基本性质:
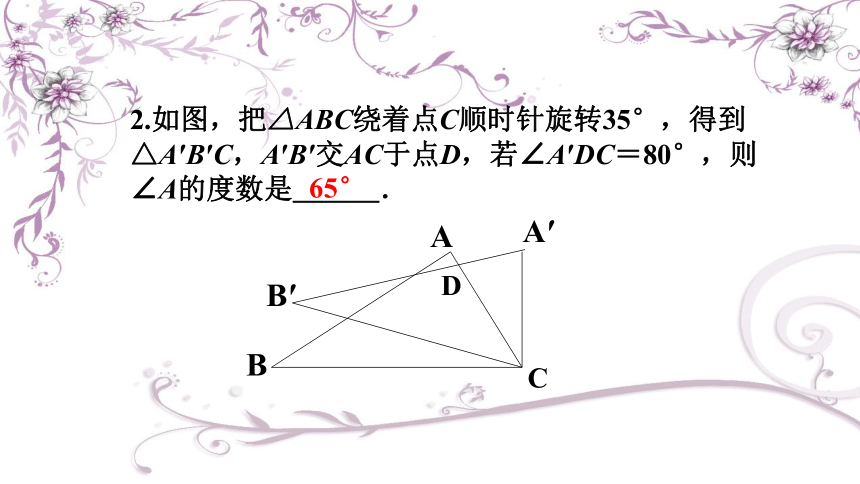
2.如图,把△ABC绕着点C顺时针旋转35°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=80°,则∠A的度数是___.
A′
A
B
B′
C
D
65°
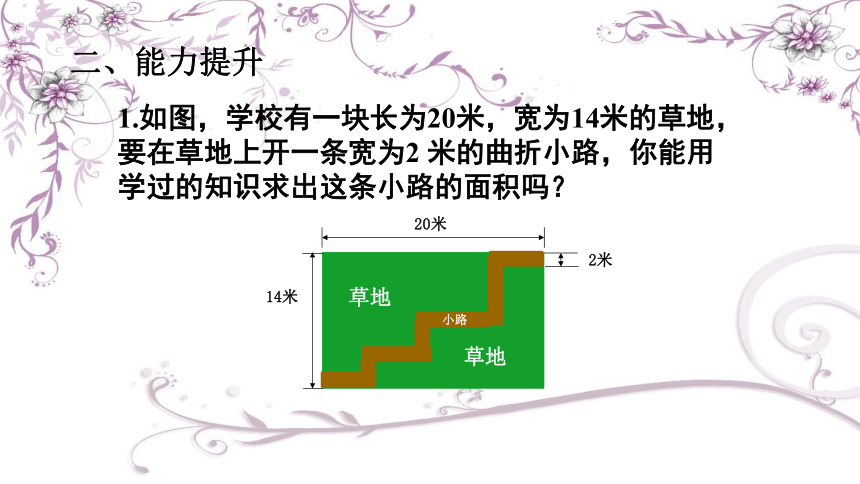
二、能力提升
1.如图,学校有一块长为20米,宽为14米的草地,要在草地上开一条宽为2 米的曲折小路,你能用学过的知识求出这条小路的面积吗?
20米
14米
草地
草地
小路
2米
20米
14米
20米
14米
第一种解法S=20×2+14×2-2×2=64㎡
2米
2米
图1
图2
第二种解法S=20×14-(20-2)×(14-2)=64㎡
2.如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,求线段BC扫过的面积.
分析:可以运用逐量分析的方法,先分析每个条件得到其对应的结论,然后寻找它们之间的关系,从而进行突破.
∵点A,B的坐标分别为(1,0),(4,0)
∴AB=3,BC=5,
∵∠CAB=90°,
∴AC=4,
∴点C的坐标为(1,4),
当点C落在直线y=2x-6上时,
∴令y=4,得到4=2x-6,
解得x=5,
∴平移的距离BB'=CC'=5-1=4,
∴线段BC扫过的面积
S□BB'C'C=BB'·AC=4×4=16,
y=2x-6
3.(1) 如图,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
感悟:解题时,条件中若出现两条边相等且它们有公共端点,可以考虑构造以公共端点为旋转中心的旋转图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
小明在组内经过合作交流,得到了如下的解决方法:将△ACD绕点D逆时针旋转180°得到△EBD,把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.
问题解决:
受到(1)的启发,你将如何解决下面问题:
(2)如图,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连结EF.
①求证:BE+CF>EF;
②若∠A=90°,探索线段BE、CF、EF之间的
等量关系,并加以证明.
①把△CFD绕点D逆时针旋转180°得到△BGD
∴∠FDG=∠CDB=180°,CF=BG,DF=DG
∵DE⊥DF,
∴EF=EG.
在△BEG中,BE+BG>EG,即BE+CF>EF.
②若∠A=90°,则∠EBC+∠FCB=90°
由①知∠FCD=∠DBG,EF=EG,
∴∠EBC+∠DBG=90°,即∠EBG=90°
∴在Rt△EBG中,BE2+BG2=EG2
∴BE2+CF2=EF2;
1.已知:如图,点P是等边△ABC内一点,PA=2,PB= ,PC=1,将△BPC绕点B逆时针旋转60°得到△BP'A,连接PP'.
(1)证明△BPP'是等边三角形;
(2)求∠PP'A的度数;
(3)求∠BPC的度数.
三、知识拓展
(1)∵△BPC绕点B逆时针旋转60°得到△BP'A,PB=
∴PB=P'B= ,∠PBP'=60°
∴△BPP'是等边三角形
(2)∵△BPP'是等边三角形
∴PP'=PB =
∵△BPC绕点B逆时针旋转60°得到△BP'A,PC=1
∴P'A=PC=1
在△PAP'中,PA=2,P'A=1,PP'=
满足P'A2+PP' 2=PA2
∴△PAP'是直角三角形
∴∠PP'A=90°
(3)∵△BPP'是等边三角形
∴∠BP'P=60° 又∠PP'A=90°
∴∠BP'A=∠BP'P+∠PP'A=150°
∵△BPC绕点B逆时针旋转60°得到△BP'A
∴∠BPC=∠BP'A=150°
四、课堂小结
你今天的收获是什么?
1、巩固了平移、旋转的定义和性质;
2、运用平移、旋转的性质解题;
3、对题目中的数学思想和方法进行归纳总结。
五、问题思考
在△ABC中,∠ACB=90°,AC=BC,点M为射线AE上任意一点(不与A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM,射线AE于点F,D.
(1)如图 1,若∠EAC=90°,
求∠NDE的度数;
在△ABC中,∠ACB=90°,AC=BC,点M为射线AE上任意一点(不与A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM,射线AE于点F,D.
如图 2,当∠EAC为锐角时,其他条件不变,(1)中的结论是否发生变化?
如图3,当∠EAC为钝角时,其他条件不变,(1)中的结论是否发生变化?
如果不变,选取其中一种情况加以证明;如果变化,请说明理由.
谢谢!
复习课
第三章 图形的平移与旋转
一、知识梳理
这个动画反映了哪种图形变换?
A
B
C
A'
B'
C'
一、平移:在平面内,把一个图形沿着某个方向移动一定的距离,这样的图形运动称为平移。
平移不改变图形的形状和大小。
平移的基本性质:
经过平移
对应点所连的线段平行(或在同一直线上)且相等;
对应线段平行(或在同一直线上)且相等;
对应角相等。
20
1.如图,将周长为16cm的△ABC沿BC方向平移2cm得到△DEF,则四边形ABFD的周长
为 cm.
D
这个动画反映了哪种图形变换?
二、旋转:在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。这个定点称为旋转中心,转动的角称为旋转角。
旋转不改变图形的形状和大小。
1.旋转图形的任意一组对应点与旋转中心的连线所成的角都等于旋转角。
2. 对应点到旋转中心的距离相等。
3. 旋转后的图形与原图形全等。
旋转的基本性质:
2.如图,把△ABC绕着点C顺时针旋转35°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=80°,则∠A的度数是___.
A′
A
B
B′
C
D
65°
二、能力提升
1.如图,学校有一块长为20米,宽为14米的草地,要在草地上开一条宽为2 米的曲折小路,你能用学过的知识求出这条小路的面积吗?
20米
14米
草地
草地
小路
2米
20米
14米
20米
14米
第一种解法S=20×2+14×2-2×2=64㎡
2米
2米
图1
图2
第二种解法S=20×14-(20-2)×(14-2)=64㎡
2.如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,求线段BC扫过的面积.
分析:可以运用逐量分析的方法,先分析每个条件得到其对应的结论,然后寻找它们之间的关系,从而进行突破.
∵点A,B的坐标分别为(1,0),(4,0)
∴AB=3,BC=5,
∵∠CAB=90°,
∴AC=4,
∴点C的坐标为(1,4),
当点C落在直线y=2x-6上时,
∴令y=4,得到4=2x-6,
解得x=5,
∴平移的距离BB'=CC'=5-1=4,
∴线段BC扫过的面积
S□BB'C'C=BB'·AC=4×4=16,
y=2x-6
3.(1) 如图,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
感悟:解题时,条件中若出现两条边相等且它们有公共端点,可以考虑构造以公共端点为旋转中心的旋转图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
小明在组内经过合作交流,得到了如下的解决方法:将△ACD绕点D逆时针旋转180°得到△EBD,把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.
问题解决:
受到(1)的启发,你将如何解决下面问题:
(2)如图,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连结EF.
①求证:BE+CF>EF;
②若∠A=90°,探索线段BE、CF、EF之间的
等量关系,并加以证明.
①把△CFD绕点D逆时针旋转180°得到△BGD
∴∠FDG=∠CDB=180°,CF=BG,DF=DG
∵DE⊥DF,
∴EF=EG.
在△BEG中,BE+BG>EG,即BE+CF>EF.
②若∠A=90°,则∠EBC+∠FCB=90°
由①知∠FCD=∠DBG,EF=EG,
∴∠EBC+∠DBG=90°,即∠EBG=90°
∴在Rt△EBG中,BE2+BG2=EG2
∴BE2+CF2=EF2;
1.已知:如图,点P是等边△ABC内一点,PA=2,PB= ,PC=1,将△BPC绕点B逆时针旋转60°得到△BP'A,连接PP'.
(1)证明△BPP'是等边三角形;
(2)求∠PP'A的度数;
(3)求∠BPC的度数.
三、知识拓展
(1)∵△BPC绕点B逆时针旋转60°得到△BP'A,PB=
∴PB=P'B= ,∠PBP'=60°
∴△BPP'是等边三角形
(2)∵△BPP'是等边三角形
∴PP'=PB =
∵△BPC绕点B逆时针旋转60°得到△BP'A,PC=1
∴P'A=PC=1
在△PAP'中,PA=2,P'A=1,PP'=
满足P'A2+PP' 2=PA2
∴△PAP'是直角三角形
∴∠PP'A=90°
(3)∵△BPP'是等边三角形
∴∠BP'P=60° 又∠PP'A=90°
∴∠BP'A=∠BP'P+∠PP'A=150°
∵△BPC绕点B逆时针旋转60°得到△BP'A
∴∠BPC=∠BP'A=150°
四、课堂小结
你今天的收获是什么?
1、巩固了平移、旋转的定义和性质;
2、运用平移、旋转的性质解题;
3、对题目中的数学思想和方法进行归纳总结。
五、问题思考
在△ABC中,∠ACB=90°,AC=BC,点M为射线AE上任意一点(不与A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM,射线AE于点F,D.
(1)如图 1,若∠EAC=90°,
求∠NDE的度数;
在△ABC中,∠ACB=90°,AC=BC,点M为射线AE上任意一点(不与A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM,射线AE于点F,D.
如图 2,当∠EAC为锐角时,其他条件不变,(1)中的结论是否发生变化?
如图3,当∠EAC为钝角时,其他条件不变,(1)中的结论是否发生变化?
如果不变,选取其中一种情况加以证明;如果变化,请说明理由.
谢谢!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
