北师大版八年级下册数学《回顾与思考第四章 《因式分解》— 复习课》课件 (共31张PPT)
文档属性
| 名称 | 北师大版八年级下册数学《回顾与思考第四章 《因式分解》— 复习课》课件 (共31张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 12:50:35 | ||
图片预览







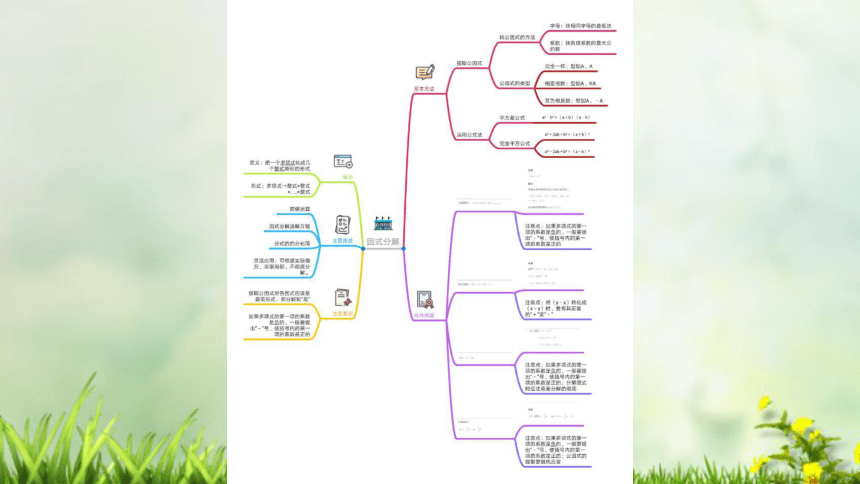
文档简介
《因式分解》— 复习课
北师大版
数学八年级下册第四章
一、 总体回顾 初成体系
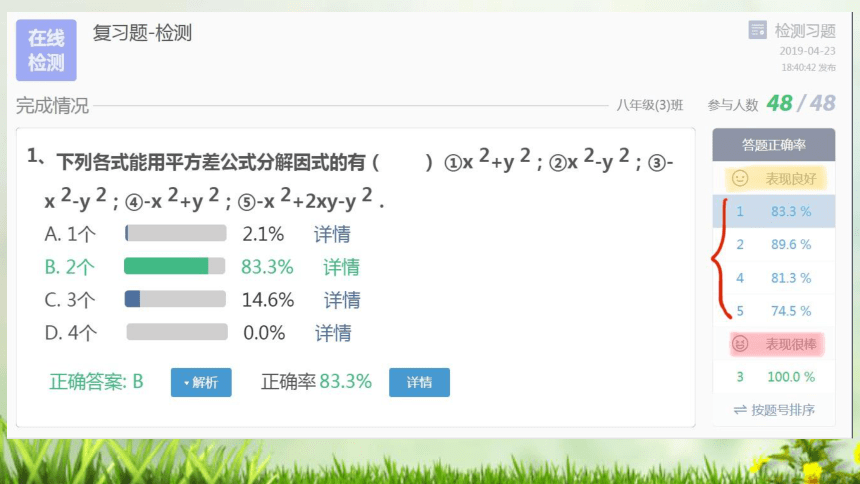
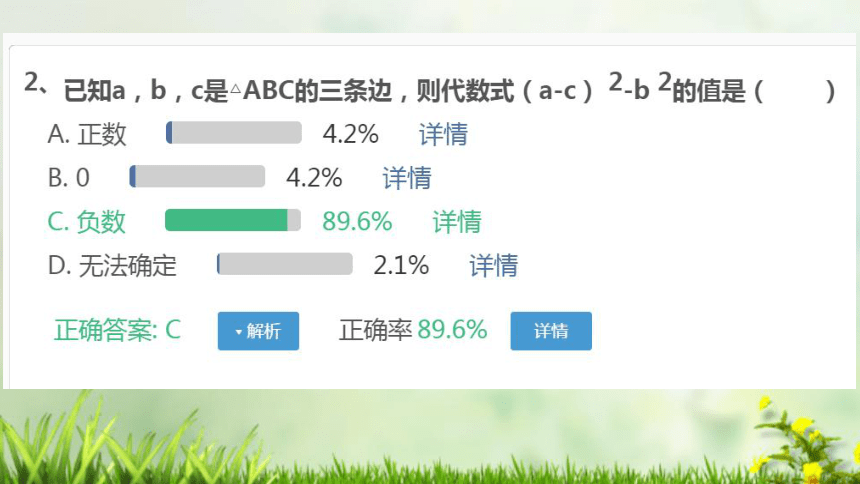
网络在线测试结果
网络学习空间
任务展示
一、 总体回顾 初成体系
网络在线测试结果
网络学习空间
任务展示
班级圈留言
张婉晴
芦汇馨
王勇超
多项式中第一项有负号的要先提取负号,以免出现符号错误。先提公因式,再套公式(完全平方与平方差切记不要搞混)。若没有公式可套,可以分组(配方)。一定要步步信心、仔细,以免分解不全。
因式分解,首先提取公因式,其次考虑用公式,十字相乘排第三,分组分解排第四,几法若都行不通,拆项添项试一试。
套公式时,公因式可以是多项式也可以是单项式。
一、 总体回顾 初成体系
网络在线测试结果
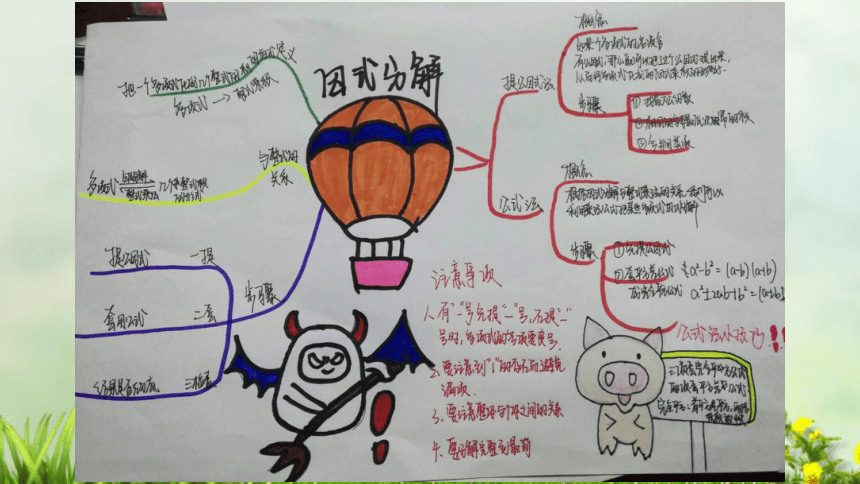
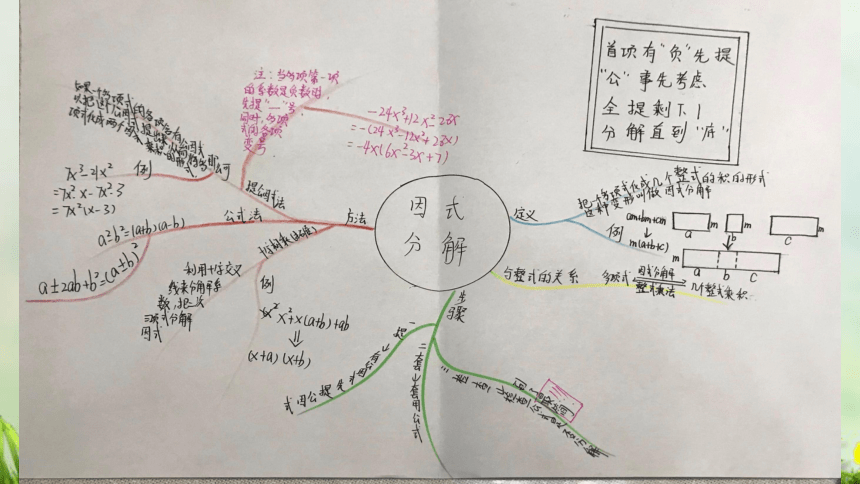
优秀思维导图展示
网络学习空间
任务展示
班级圈留言
下列式子从左到右的变形中是分解因式的为( )
B
A选项没有化成几个整式的积的形式;
C选项属于整式乘法;
D选项没有化成几个整式的积的形式.
二、纠错练习 健全体系
下列各式的因式分解是否正确?
若不正确,应怎样改正?
×
解:原式=2x(x2-2x+1)
=2x(x-1)2
×
解:原式=4m2-36
=4(m2-9)
=4(m+3)(m-3)
不要“漏项”
有公因式
先提公因式
×
解:原式=y(4xy-4x2-y2)
=-y(4x2+y2-4xy)
=-y(2x-y)2
×
(a-b)2n=(b-a)2n
(a-b)2n+1=-(b-a)2n+1
解:原式=mn(m-n)-m(m-n)2
=m(m-n)(n-m+n)
=m(m-n)(2n-m)
套公式前
可先变形
×
解:原式=(p2 +1)(p+1)(p-1)
×
解:原式=(a-4)(a+2)
“分解彻底”
要“符合定义”
×
解:原式=[3-(a+b)]2
=(3-a-b)2
√
要有“整体”思想
可利用整式的乘法检验因式分解
例一、将下列各式因式分解
三、典型例题 提升能力
5a2-20b
a4-8a2b2+16b4
(2n+1)2-(n+2)2
1- x2-2xy-y2
(x2-4)2-10(x2-4)+25
=5(a2-4b)
=(a+2b)2(a-2b)2
=(1+x+y)(1-x-y)
=3(n+1)(n-1)
=(x+3)2(x-3)2
1
有公因式先提公因式
2
再看能否套用公式
3
检查是否分解彻底与正确
因式分解的步骤:
例二、用简便方法计算
(1)20182-2018×4038+20192
(2) 9992+999+6852-3152
解:原式=20182-2 × 2018×2019+20192
=(2018-2019)2
=1
解:原式=999×(999+1)+(685-315)×(685+315)
=999×1000+370×1000
=999000+370000
=1369000
例三、通过本章学习,我们知道可以用拼图来解释一些多项式的因式分解。假设我们有足够多的长方形和正方形卡片,如下图:
1
a
a
2
b
b
3
b
a
(1)如果取1号、2号、3号卡片分别为1张、2张、3张,你能通过拼图形象地说明多项式a2+3ab+2b2的因式分解吗?拼出图形,并根据图形写出因式分解的结果。
a2+3ab+2b2=(a+2b)(a+b)
(2)如果取1号、2号、3号卡片分别为1张、3张、4张,你能通过拼图形象地说明一个怎样的多项式的因式分解?拼出图形,并根据图形写出因式分解的结果。
a2+4ab+3b2=(a+b)(a+3b)
通过复习这节课你有哪些收获与感受?说出来与大家一起分享!
四、感悟收获 完善体系
因 式 分 解
概念
方法
思想
应用
步骤
课后作业
Thank you for watching
业精于勤荒于嬉;
行成于思毁于随。
谢谢!
北师大版
数学八年级下册第四章
一、 总体回顾 初成体系
网络在线测试结果
网络学习空间
任务展示
一、 总体回顾 初成体系
网络在线测试结果
网络学习空间
任务展示
班级圈留言
张婉晴
芦汇馨
王勇超
多项式中第一项有负号的要先提取负号,以免出现符号错误。先提公因式,再套公式(完全平方与平方差切记不要搞混)。若没有公式可套,可以分组(配方)。一定要步步信心、仔细,以免分解不全。
因式分解,首先提取公因式,其次考虑用公式,十字相乘排第三,分组分解排第四,几法若都行不通,拆项添项试一试。
套公式时,公因式可以是多项式也可以是单项式。
一、 总体回顾 初成体系
网络在线测试结果
优秀思维导图展示
网络学习空间
任务展示
班级圈留言
下列式子从左到右的变形中是分解因式的为( )
B
A选项没有化成几个整式的积的形式;
C选项属于整式乘法;
D选项没有化成几个整式的积的形式.
二、纠错练习 健全体系
下列各式的因式分解是否正确?
若不正确,应怎样改正?
×
解:原式=2x(x2-2x+1)
=2x(x-1)2
×
解:原式=4m2-36
=4(m2-9)
=4(m+3)(m-3)
不要“漏项”
有公因式
先提公因式
×
解:原式=y(4xy-4x2-y2)
=-y(4x2+y2-4xy)
=-y(2x-y)2
×
(a-b)2n=(b-a)2n
(a-b)2n+1=-(b-a)2n+1
解:原式=mn(m-n)-m(m-n)2
=m(m-n)(n-m+n)
=m(m-n)(2n-m)
套公式前
可先变形
×
解:原式=(p2 +1)(p+1)(p-1)
×
解:原式=(a-4)(a+2)
“分解彻底”
要“符合定义”
×
解:原式=[3-(a+b)]2
=(3-a-b)2
√
要有“整体”思想
可利用整式的乘法检验因式分解
例一、将下列各式因式分解
三、典型例题 提升能力
5a2-20b
a4-8a2b2+16b4
(2n+1)2-(n+2)2
1- x2-2xy-y2
(x2-4)2-10(x2-4)+25
=5(a2-4b)
=(a+2b)2(a-2b)2
=(1+x+y)(1-x-y)
=3(n+1)(n-1)
=(x+3)2(x-3)2
1
有公因式先提公因式
2
再看能否套用公式
3
检查是否分解彻底与正确
因式分解的步骤:
例二、用简便方法计算
(1)20182-2018×4038+20192
(2) 9992+999+6852-3152
解:原式=20182-2 × 2018×2019+20192
=(2018-2019)2
=1
解:原式=999×(999+1)+(685-315)×(685+315)
=999×1000+370×1000
=999000+370000
=1369000
例三、通过本章学习,我们知道可以用拼图来解释一些多项式的因式分解。假设我们有足够多的长方形和正方形卡片,如下图:
1
a
a
2
b
b
3
b
a
(1)如果取1号、2号、3号卡片分别为1张、2张、3张,你能通过拼图形象地说明多项式a2+3ab+2b2的因式分解吗?拼出图形,并根据图形写出因式分解的结果。
a2+3ab+2b2=(a+2b)(a+b)
(2)如果取1号、2号、3号卡片分别为1张、3张、4张,你能通过拼图形象地说明一个怎样的多项式的因式分解?拼出图形,并根据图形写出因式分解的结果。
a2+4ab+3b2=(a+b)(a+3b)
通过复习这节课你有哪些收获与感受?说出来与大家一起分享!
四、感悟收获 完善体系
因 式 分 解
概念
方法
思想
应用
步骤
课后作业
Thank you for watching
业精于勤荒于嬉;
行成于思毁于随。
谢谢!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
