北师大版八年级下册数学《回顾与思考第四章 因式分解复习课》课件 (共19张PPT)
文档属性
| 名称 | 北师大版八年级下册数学《回顾与思考第四章 因式分解复习课》课件 (共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 12:53:34 | ||
图片预览






文档简介
因式分解复习课
学习目标
一、整理学生出现的错题,归类分析错误原因,形成因式分解的注意事项。
二、因式分解的典型题训练。
三、运用因式分解解决实际问题。
a2+2ab+b2=(a+b)2
a2-2ab+b2=(a-b)2
a2-b2=(a+b)(a-b)
涉及的知识点
把一个多项式写成几个整式的积的形式叫做因式分解.因式分解是整式乘法的逆变形。
二、因式分解有哪些方法?
(一)提公因式法;
(二)运用公式法:
一、什么叫因式分解?
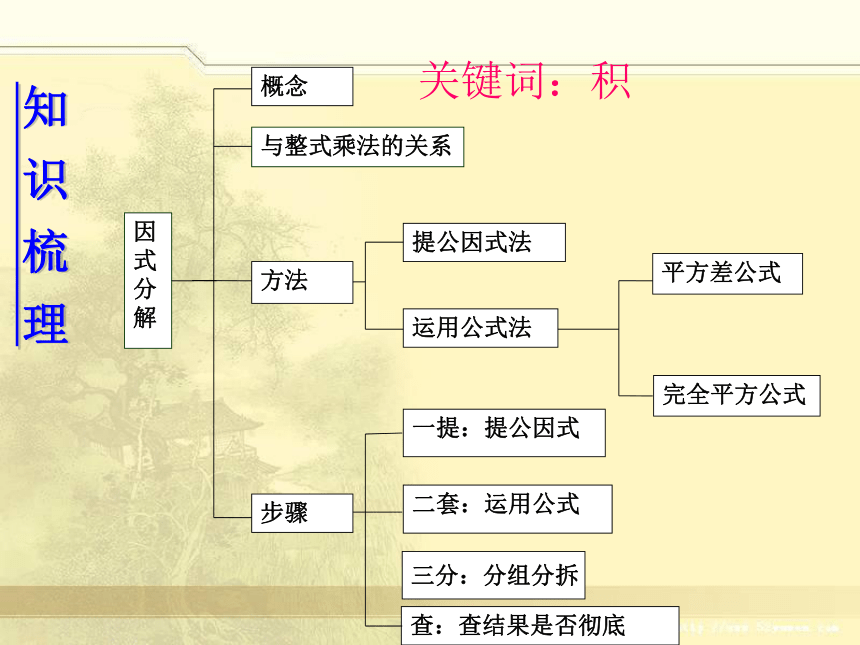
知 识 梳 理
因式分解
概念
与整式乘法的关系
方法
提公因式法
运用公式法
平方差公式
完全平方公式
步骤
一提:提公因式
二套:运用公式
查:查结果是否彻底
关键词:积
三分:分组分拆
一提:提取公因式
二套:套完全平方公式或者平方差公式
三分:分组与分拆
四查:查是否分解彻底,与原式是否相等
基本步骤
错题分析:
一、分解不彻底
二、完全平方式丢解(区别于完全平方公式)
三、因式分解与整式乘法综合运用不过关
四、分解因式的灵活应用能力欠缺
一、分解不彻底
1题:16-x4
2题:9(x-y)2-25(x+y)2
二、完全平方式严重丢解
若9x2+kxy+y2是完全平方式,
则k=
巩固练习
4x2-kx+25是完全平方式,则k=
三、因式分解与整式乘法综合运用不过关
(x-y)2-4(x-y-1)
方法指导 :
整体思想,转化思想
已知:a、 b、 c为三角形的三条边,且满足a?+b?+c?-ab-bc-ac=0,证明:三角形是等边三角形
四、分解因式的灵活应用能力欠缺
数学思想:
数形结合
1.下列各式从左到右的变形中,哪些是因式分解?为什么?
(3)
巩固练习:
2.下列多项式能分解因式的( )
B
3、把下列各式分解因式:
4.计算:
5.因式分解:
3ab2+6a2b+3a3
通过复习这节课你有那些新的收获与感受?
说出来与大家一起分享!
1、改正错题
2、整理典型习题
3、挑选同类型习题,巩固练习
作业:
课内小结:
谈谈本节课收获
学习目标
一、整理学生出现的错题,归类分析错误原因,形成因式分解的注意事项。
二、因式分解的典型题训练。
三、运用因式分解解决实际问题。
a2+2ab+b2=(a+b)2
a2-2ab+b2=(a-b)2
a2-b2=(a+b)(a-b)
涉及的知识点
把一个多项式写成几个整式的积的形式叫做因式分解.因式分解是整式乘法的逆变形。
二、因式分解有哪些方法?
(一)提公因式法;
(二)运用公式法:
一、什么叫因式分解?
知 识 梳 理
因式分解
概念
与整式乘法的关系
方法
提公因式法
运用公式法
平方差公式
完全平方公式
步骤
一提:提公因式
二套:运用公式
查:查结果是否彻底
关键词:积
三分:分组分拆
一提:提取公因式
二套:套完全平方公式或者平方差公式
三分:分组与分拆
四查:查是否分解彻底,与原式是否相等
基本步骤
错题分析:
一、分解不彻底
二、完全平方式丢解(区别于完全平方公式)
三、因式分解与整式乘法综合运用不过关
四、分解因式的灵活应用能力欠缺
一、分解不彻底
1题:16-x4
2题:9(x-y)2-25(x+y)2
二、完全平方式严重丢解
若9x2+kxy+y2是完全平方式,
则k=
巩固练习
4x2-kx+25是完全平方式,则k=
三、因式分解与整式乘法综合运用不过关
(x-y)2-4(x-y-1)
方法指导 :
整体思想,转化思想
已知:a、 b、 c为三角形的三条边,且满足a?+b?+c?-ab-bc-ac=0,证明:三角形是等边三角形
四、分解因式的灵活应用能力欠缺
数学思想:
数形结合
1.下列各式从左到右的变形中,哪些是因式分解?为什么?
(3)
巩固练习:
2.下列多项式能分解因式的( )
B
3、把下列各式分解因式:
4.计算:
5.因式分解:
3ab2+6a2b+3a3
通过复习这节课你有那些新的收获与感受?
说出来与大家一起分享!
1、改正错题
2、整理典型习题
3、挑选同类型习题,巩固练习
作业:
课内小结:
谈谈本节课收获
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
