北师大版八年级下册数学2.5一元一次不等式与一次函数图象的关系 课件 (共20张PPT)
文档属性
| 名称 | 北师大版八年级下册数学2.5一元一次不等式与一次函数图象的关系 课件 (共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 00:00:00 | ||
图片预览




文档简介
创设情景,引入新知
y=2x-5
锦州北镇市沟帮子中学在市教育局开展的“学会生存”作为必修课活动中,率先垂范,先后开展了“防火、防震”逃生演练,“防止踩踏”等演练。
在周一的“防止踩踏”疏散课上,八年(16)班的同学在警报响起3秒后疏散距离y(米)与时间x(秒)满足关系式:
方程、不等式及函数是数学的三个基本模型,它们之间有什么关系呢?
学习目标
1、理解一次函数图象与一元一次不等式 的关系。
2、能够用图像法解一元一次不等式。
3、理解两种方法的关系,会选择适当的方法解决函数问题。
*
创设情景,引入新知
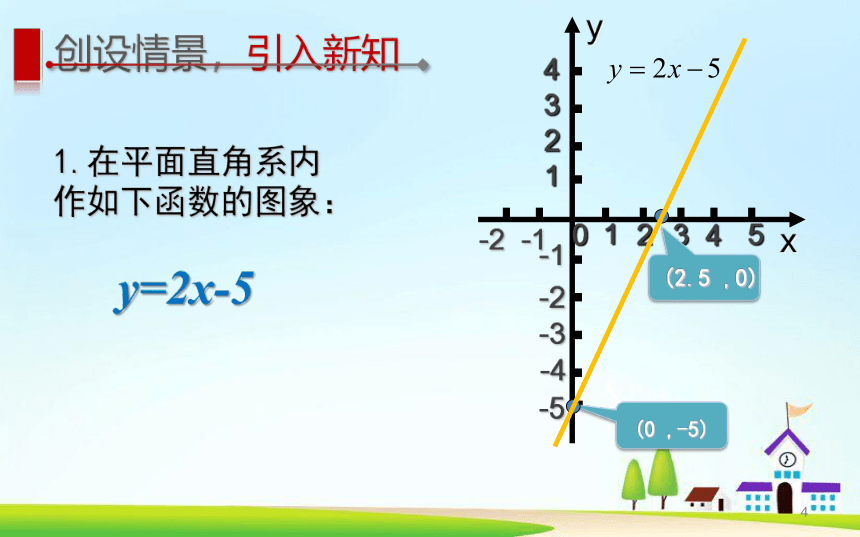
1.在平面直角系内 作如下函数的图象:
x
y
0
1
2
3
4
-2 -1
5
1
2
3
4
-1
-2
-3
-4
-5
(2.5 ,0)
(0 ,-5)
y=2x-5
创设情景,引入新知
x
y
0
1
2
3
4
-2 -1
5
1
2
3
4
-1
-2
-3
-4
-5
(2.5 , 0)
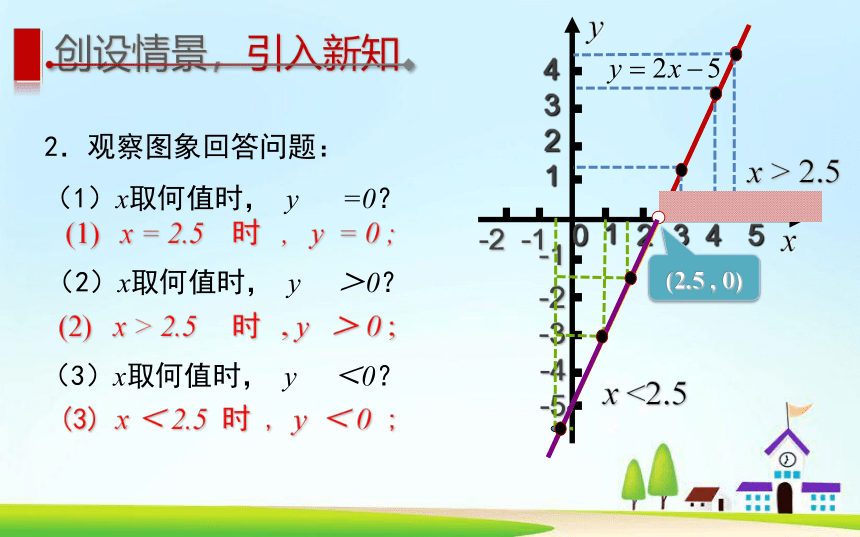
(3)x取何值时, y <0?
(2)x取何值时, y >0?
2.观察图象回答问题:
(1)x取何值时, y =0?
创设情景,引入新知
x
y
0
1
2
3
4
-2 -1
5
1
2
3
4
-1
-2
-3
-4
-5
(2.5 , 0)
(3)x取何值时, y <0?
(2)x取何值时, y >0?
2.观察图象回答问题:
(1)x取何值时, y =0?
(1) x = 2.5 时 , y = 0 ;
(3) x < 2.5 时 , y < 0 ;
(2) x > 2.5 时 , y > 0 ;
x > 2.5
x <2.5
创设情景,引入新知
x
y
0
1
2
3
4
-2 -1
5
1
2
3
4
-1
-2
-3
-4
-5
(2.5 , 0)
(3)x取何值时, y <0?
(2)x取何值时, y >0?
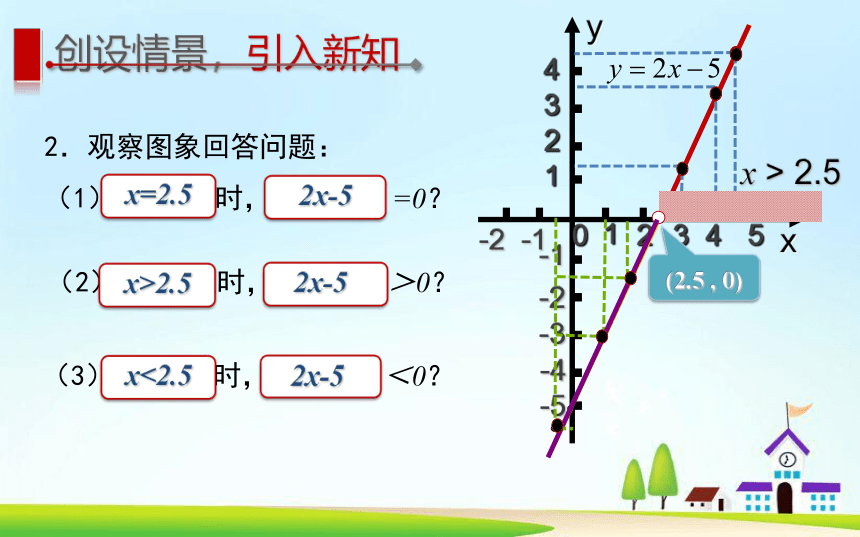
2.观察图象回答问题:
(1)x取何值时, y =0?
x > 2.5
x=2.5
2x-5
x>2.5
x<2.5
2x-5
2x-5
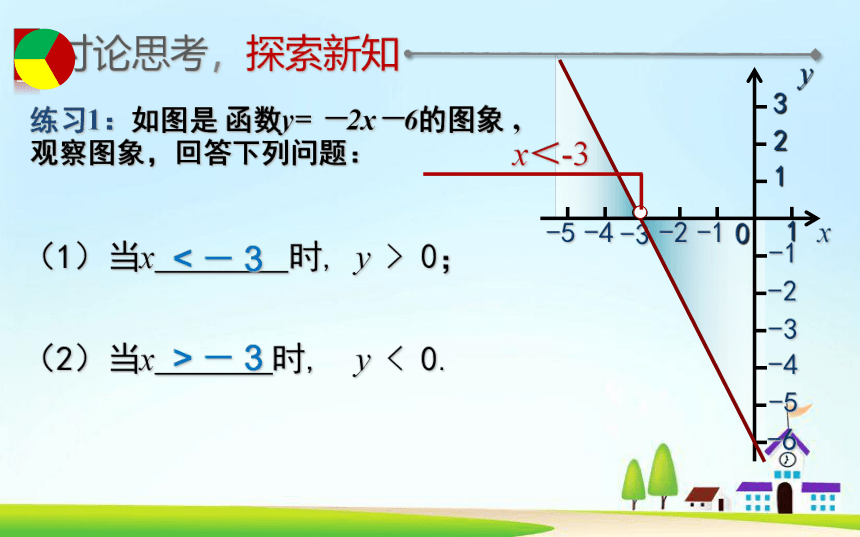
练习1:如图是 函数y= -2x-6的图象 ,
观察图象,回答下列问题:
x
y
-1
-2
-3
-4
-5
1
-1
-2
-3
-4
-5
-6
1
2
3
0
(1)当x 时, y > 0;
(2)当x 时, y < 0.
< - 3
> - 3
讨论思考,探索新知
x<-3
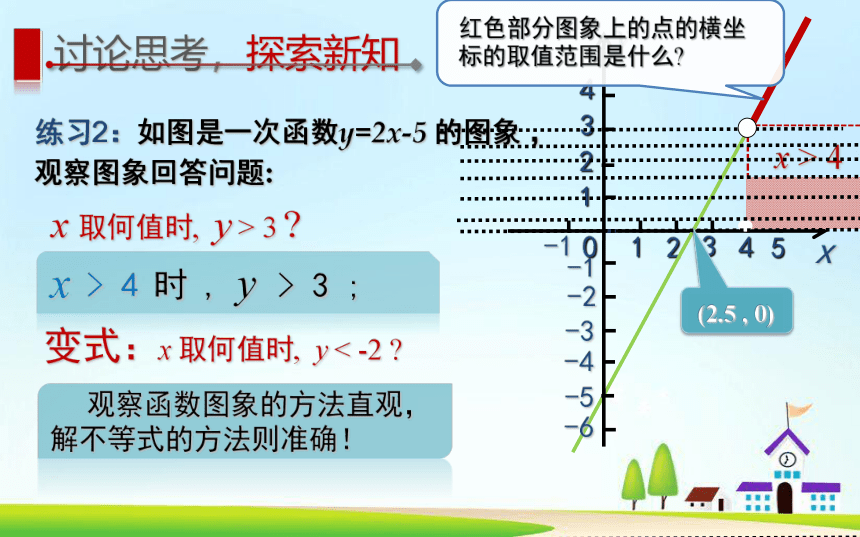
x > 4 时 , y > 3 ;
讨论思考,探索新知
x 取何值时, y > 3 ?
练习2:如图是一次函数y=2x-5 的图象 ,
观察图象回答问题:
0
x
1
2
3
-1
4
1
-1
-2
3
-4
-3
2
-5
-6
y
5
4
变式:x 取何值时, y < -2 ?
观察函数图象的方法直观,解不等式的方法则准确!
x > 4
红色部分图象上的点的横坐标的取值范围是什么?
转化思想:
一次函数问题
一次不等式(方程)问题
转化
求函数问题的方法:
(1)图象法:
画出函数图象解决函数问题;
(2)列式法:
列不等式(方程)求解集解决函数问题.
深入探究,多维理解
问题二:在“问题一”图中添加一条直线:
结合所画图象回答问题:
(1)x取何值时,y1= y2?
(2)x取何值时,y1>y2?
(3)x取何值时,y1< y2?
x=4
x<4
x>4
0
x
1
2
3
-1
4
1
-1
-2
3
-4
-3
2
-5
-6
y
5
4
-2
深入探究,多维理解
问题二:在“问题一”图中添加一条直线:
结合所画图象回答问题:
(1)x取何值时,y1= y2?
(2)x取何值时,y1>y2?
(3)x取何值时,y1< y2?
x=4
x<4
x>4
0
x
1
2
3
-1
4
1
-1
-2
3
-4
-3
2
-5
-6
y
5
4
-2
拓展应用,解决问题
问题三:在疏散演习的过程中,老师将八年(16)班的同学分成A、B两组,A组出发时B组已跑9 米。已知B组每秒跑3 米, A组每秒跑4米。
1、A组疏散的时间为x (秒), A组与B组同学疏散的路程分别为 y1、 y2 (米),列出y1、 y2与x的函数关系式。
y1= ,y2 = .
3x+9
4x
拓展应用,解决问题
1.解:
y1= ,y2 = .
3x+9
4x
2.如图,在同一平面直角坐标系内分别作出函数y1=4x,y2=3x+9的图象。
x
y
-2
0
10
8
6
4
2
100
90
80
70
60
50
40
30
20
10
(秒)
(米)
A组
B组
y2
y1
(9,36)
小组活动:
我问问题你来答!
拓展应用,解决问题
练 习 3
如图是一次函数y=kx+b(k≠0)的图象,则关于x的方程kx+b=0的解为 ;关于x的不等式kx+b>0的解集为 ;关于x的不等式kx+b<0的解集为解为 .
y
x
O
练 习 4
如图 ,直线l1与l2交于P点,当x在什么范围内取值时y1>y2?
y
x
O
3
4
P
反思小结,培养能力
1、通过本节课,你学到了什么知识?
2、你体会到了什么数学思想??
1.转化思想:
一次函数问题
一次不等式问题
转化
2.求函数问题的方法:
(1)图象法:
画出函数图象解决函数问题;
(2)列式法:
列不等式求解集解决函数问题.
课堂小结
课后作业,自主学习
1、课本P51 习题2.6?
2、如右图是函数y1=2x-4与y2=-2x+8的图象,回答下列问题:
(1)x取何值时,y1>0?
(2)x取何值时,y2>0?
(3) (选做) x取何值时,y1>0与y2>0同时成立?
(4) (选做)若y1=k1x+b1,y2=k2x+b2,C(3,2),x取何值时,y1> y2?
y=2x-5
锦州北镇市沟帮子中学在市教育局开展的“学会生存”作为必修课活动中,率先垂范,先后开展了“防火、防震”逃生演练,“防止踩踏”等演练。
在周一的“防止踩踏”疏散课上,八年(16)班的同学在警报响起3秒后疏散距离y(米)与时间x(秒)满足关系式:
方程、不等式及函数是数学的三个基本模型,它们之间有什么关系呢?
学习目标
1、理解一次函数图象与一元一次不等式 的关系。
2、能够用图像法解一元一次不等式。
3、理解两种方法的关系,会选择适当的方法解决函数问题。
*
创设情景,引入新知
1.在平面直角系内 作如下函数的图象:
x
y
0
1
2
3
4
-2 -1
5
1
2
3
4
-1
-2
-3
-4
-5
(2.5 ,0)
(0 ,-5)
y=2x-5
创设情景,引入新知
x
y
0
1
2
3
4
-2 -1
5
1
2
3
4
-1
-2
-3
-4
-5
(2.5 , 0)
(3)x取何值时, y <0?
(2)x取何值时, y >0?
2.观察图象回答问题:
(1)x取何值时, y =0?
创设情景,引入新知
x
y
0
1
2
3
4
-2 -1
5
1
2
3
4
-1
-2
-3
-4
-5
(2.5 , 0)
(3)x取何值时, y <0?
(2)x取何值时, y >0?
2.观察图象回答问题:
(1)x取何值时, y =0?
(1) x = 2.5 时 , y = 0 ;
(3) x < 2.5 时 , y < 0 ;
(2) x > 2.5 时 , y > 0 ;
x > 2.5
x <2.5
创设情景,引入新知
x
y
0
1
2
3
4
-2 -1
5
1
2
3
4
-1
-2
-3
-4
-5
(2.5 , 0)
(3)x取何值时, y <0?
(2)x取何值时, y >0?
2.观察图象回答问题:
(1)x取何值时, y =0?
x > 2.5
x=2.5
2x-5
x>2.5
x<2.5
2x-5
2x-5
练习1:如图是 函数y= -2x-6的图象 ,
观察图象,回答下列问题:
x
y
-1
-2
-3
-4
-5
1
-1
-2
-3
-4
-5
-6
1
2
3
0
(1)当x 时, y > 0;
(2)当x 时, y < 0.
< - 3
> - 3
讨论思考,探索新知
x<-3
x > 4 时 , y > 3 ;
讨论思考,探索新知
x 取何值时, y > 3 ?
练习2:如图是一次函数y=2x-5 的图象 ,
观察图象回答问题:
0
x
1
2
3
-1
4
1
-1
-2
3
-4
-3
2
-5
-6
y
5
4
变式:x 取何值时, y < -2 ?
观察函数图象的方法直观,解不等式的方法则准确!
x > 4
红色部分图象上的点的横坐标的取值范围是什么?
转化思想:
一次函数问题
一次不等式(方程)问题
转化
求函数问题的方法:
(1)图象法:
画出函数图象解决函数问题;
(2)列式法:
列不等式(方程)求解集解决函数问题.
深入探究,多维理解
问题二:在“问题一”图中添加一条直线:
结合所画图象回答问题:
(1)x取何值时,y1= y2?
(2)x取何值时,y1>y2?
(3)x取何值时,y1< y2?
x=4
x<4
x>4
0
x
1
2
3
-1
4
1
-1
-2
3
-4
-3
2
-5
-6
y
5
4
-2
深入探究,多维理解
问题二:在“问题一”图中添加一条直线:
结合所画图象回答问题:
(1)x取何值时,y1= y2?
(2)x取何值时,y1>y2?
(3)x取何值时,y1< y2?
x=4
x<4
x>4
0
x
1
2
3
-1
4
1
-1
-2
3
-4
-3
2
-5
-6
y
5
4
-2
拓展应用,解决问题
问题三:在疏散演习的过程中,老师将八年(16)班的同学分成A、B两组,A组出发时B组已跑9 米。已知B组每秒跑3 米, A组每秒跑4米。
1、A组疏散的时间为x (秒), A组与B组同学疏散的路程分别为 y1、 y2 (米),列出y1、 y2与x的函数关系式。
y1= ,y2 = .
3x+9
4x
拓展应用,解决问题
1.解:
y1= ,y2 = .
3x+9
4x
2.如图,在同一平面直角坐标系内分别作出函数y1=4x,y2=3x+9的图象。
x
y
-2
0
10
8
6
4
2
100
90
80
70
60
50
40
30
20
10
(秒)
(米)
A组
B组
y2
y1
(9,36)
小组活动:
我问问题你来答!
拓展应用,解决问题
练 习 3
如图是一次函数y=kx+b(k≠0)的图象,则关于x的方程kx+b=0的解为 ;关于x的不等式kx+b>0的解集为 ;关于x的不等式kx+b<0的解集为解为 .
y
x
O
练 习 4
如图 ,直线l1与l2交于P点,当x在什么范围内取值时y1>y2?
y
x
O
3
4
P
反思小结,培养能力
1、通过本节课,你学到了什么知识?
2、你体会到了什么数学思想??
1.转化思想:
一次函数问题
一次不等式问题
转化
2.求函数问题的方法:
(1)图象法:
画出函数图象解决函数问题;
(2)列式法:
列不等式求解集解决函数问题.
课堂小结
课后作业,自主学习
1、课本P51 习题2.6?
2、如右图是函数y1=2x-4与y2=-2x+8的图象,回答下列问题:
(1)x取何值时,y1>0?
(2)x取何值时,y2>0?
(3) (选做) x取何值时,y1>0与y2>0同时成立?
(4) (选做)若y1=k1x+b1,y2=k2x+b2,C(3,2),x取何值时,y1> y2?
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
