北师大版八年级下册数学4.3第2课时 完全平方公式课件 (共20张PPT)
文档属性
| 名称 | 北师大版八年级下册数学4.3第2课时 完全平方公式课件 (共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 730.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 00:00:00 | ||
图片预览







文档简介
第四章 因式分解
4.3 公式法
第2课时 完全平方公式
1.因式分解:
把一个多项式转化为几个整式的积的形式.
2.我们已经学过哪些因式分解的方法?
1.提公因式法
2.平方差公式
a2-b2=(a+b)(a-b)
1、把下列各式因式分解:
(2)ax4 - ax2
(1)16a2 – 9b2
=(4a)2 –(3b)2
=(4a+3b) (4a-3b)
=ax2(x2-1)
=ax2(x+1)(x-1)
2、你能用前面学过的方法把多项式x2+10x+25因式分解吗?
学习目标
1.理解并掌握用完全平方公式分解因式.(重点)
2.学会观察多项式的特点,恰当地安排步骤,恰当地选用不同方法分解因式.(难点)
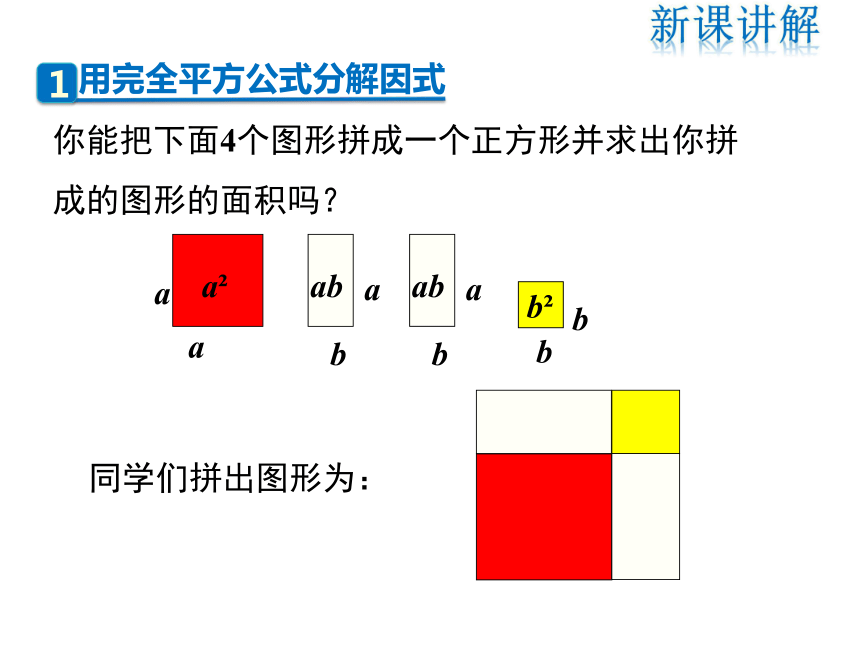
你能把下面4个图形拼成一个正方形并求出你拼成的图形的面积吗?
同学们拼出图形为:
a
a
b
b
a
b
a
b
ab
a?
b?
ab
用完全平方公式分解因式
1
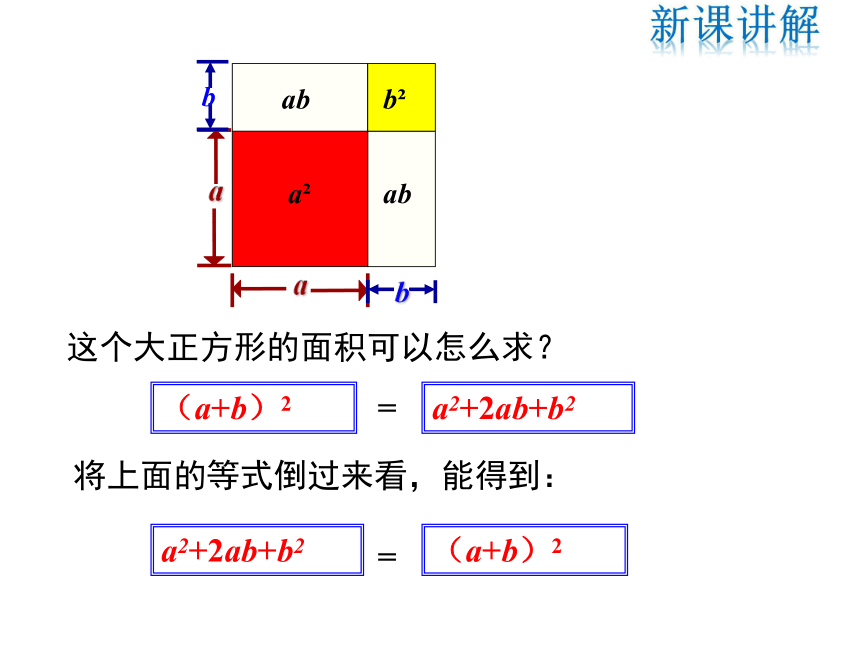
这个大正方形的面积可以怎么求?
a2+2ab+b2
(a+b)2
=
a
b
a
b
a?
ab
ab
b?
(a+b)2
a2+2ab+b2
=
将上面的等式倒过来看,能得到:
a2+2ab+b2
a2-2ab+b2
我们把a?+2ab+b?和a?-2ab+b?这样的式子叫作完全平方式.
观察这两个式子:
(1)每个多项式有几项?
(2)每个多项式的第一项和第三项有什么特征?
(3)中间项和第一项,第三项有什么关系?
三项
这两项都是数或式的平方,并且符号相同
是第一项和第三项底数的积的±2倍
完全平方式的特点:
1.必须是三项式(或可以看成三项的);
2.有两个同号的数或式的平方;
3.中间有两底数之积的±2倍.
完全平方式:
简记口诀:
首平方,尾平方,首尾两倍在中央.
凡具备这些特点的三项式,就是完全平方式,将它写成完全平方形式,便实现了因式分解.
2
a
b
+b2
±
=(a ± b)?
a2
首2
+尾2
±2×首×尾
(首±尾)2
两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方.
3.a?+4ab+4b?=( )?+2· ( ) ·( )+( )?=( )?
2.m?-6m+9=( )? - 2· ( ) ·( )+( )? =( )?
1. x?+4x+4= ( )? +2·( )·( )+( )? =( )?
x
2
x + 2
a
a 2b
a + 2b
2b
对照 a?±2ab+b?=(a±b)?,填空:
m
m - 3
3
x
2
m
3
下列各式是不是完全平方式?
(1)a2-4a+4; (2)1+4a?;
(3)4b2+4b-1; (4)a2+ab+b2;
(5)x2+x+0.25.
是
(2)因为它只有两项;
不是
(3)4b?与-1的符号不统一;
不是
分析:
不是
是
(4)因为ab不是a与b的积的2倍.
如果x2-6x+N是一个完全平方式,那么N是( )
A . 11 B. 9 C. -11 D. -9
B
解析:根据完全平方式的特征,中间项:
-6x=2x×(-3),故可知N=(-3)2=9.
如果x2-mx+16是一个完全平方式,那么m的值为___.
解析:∵16=(±4)2,故-m=2×(±4),m=±8.
±8
例1
练一练
分解因式:
(1)x2+14x+49; (2)(m+n)2-6(m+n)+9.
分析:(1)中, x2=x2, 49=7?,14x=2·x·7, 所以x2+14x
+49是一个完全平方式,即x2 + 14x +49= x2+ 2·x·7 + 72.
2
a
b
+b2
a2
(2)中,把(m+n)看成一个整体,所以(m+n)2-6(m+n)+9是一个完全平方式.
例2
解: (1)x2++14x +49
= (x + 7)2;
解:原式= x2 + 2·x·7 + 72
(2) (m+n)2-6(m+n)+9
解:原式=[(m+n)-3]2
=(m+n-3)2.
把下列式子分解因式
(1)m2 -12mn+36n2
解:原式=m2-2·m·6n+(6n)2
=(m-6n)2
(2)a2-2a(b+c)+(b+c)2
解:原式=a2-2·a· (b+c) + (b+c) 2
=[a- (b+c) ]2
=(a-b-c)2
把下列各式分解因式:
(1)3ax2+6axy+3ay2 ;(2)-x2-4y2+4xy.
解: (1)原式=3a(x2+2xy+y2)
=3a(x+y)2;
分析:(1)中有公因式3a,应先提出公因式,再进一步分解因式;
(2)中首项有负号,一般先利用添括号法则,将其变形为-(x2-4xy+4y2),然后再利用公式分解因式.
(2)原式=-(x2-4xy+4y2)
=-(x-2y)2.
例3
因式分解:
(1)-3a2x2+24a2x-48a2;
(2)(a2+4)2-16a2.
=(a2+4+4a)(a2+4-4a)
解:(1)原式=-3a2(x2-8x+16)
=-3a2(x-4)2;
(2)原式=(a2+4)2-(4a)2
=(a+2)2(a-2)2.
有公因式要先提公因式
要检查每一个多项式的因式,看能否继续分解.
练一练
(1)形如________________形式的多项式可以用完全平方公式分解因式。
(3)因式分解要_________.
(2)因式分解通常首先考虑______________方法。
提取公因式法
彻底
完全平方公式分解因式
公式
a2±2ab+b2=(a±b)2
特点
(1)要求多项式有三项.
(2)其中两项同号,且都可以写成某数或式的平方,另一项则是这两数或式的乘积的2倍,符号可正可负.
4.3 公式法
第2课时 完全平方公式
1.因式分解:
把一个多项式转化为几个整式的积的形式.
2.我们已经学过哪些因式分解的方法?
1.提公因式法
2.平方差公式
a2-b2=(a+b)(a-b)
1、把下列各式因式分解:
(2)ax4 - ax2
(1)16a2 – 9b2
=(4a)2 –(3b)2
=(4a+3b) (4a-3b)
=ax2(x2-1)
=ax2(x+1)(x-1)
2、你能用前面学过的方法把多项式x2+10x+25因式分解吗?
学习目标
1.理解并掌握用完全平方公式分解因式.(重点)
2.学会观察多项式的特点,恰当地安排步骤,恰当地选用不同方法分解因式.(难点)
你能把下面4个图形拼成一个正方形并求出你拼成的图形的面积吗?
同学们拼出图形为:
a
a
b
b
a
b
a
b
ab
a?
b?
ab
用完全平方公式分解因式
1
这个大正方形的面积可以怎么求?
a2+2ab+b2
(a+b)2
=
a
b
a
b
a?
ab
ab
b?
(a+b)2
a2+2ab+b2
=
将上面的等式倒过来看,能得到:
a2+2ab+b2
a2-2ab+b2
我们把a?+2ab+b?和a?-2ab+b?这样的式子叫作完全平方式.
观察这两个式子:
(1)每个多项式有几项?
(2)每个多项式的第一项和第三项有什么特征?
(3)中间项和第一项,第三项有什么关系?
三项
这两项都是数或式的平方,并且符号相同
是第一项和第三项底数的积的±2倍
完全平方式的特点:
1.必须是三项式(或可以看成三项的);
2.有两个同号的数或式的平方;
3.中间有两底数之积的±2倍.
完全平方式:
简记口诀:
首平方,尾平方,首尾两倍在中央.
凡具备这些特点的三项式,就是完全平方式,将它写成完全平方形式,便实现了因式分解.
2
a
b
+b2
±
=(a ± b)?
a2
首2
+尾2
±2×首×尾
(首±尾)2
两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方.
3.a?+4ab+4b?=( )?+2· ( ) ·( )+( )?=( )?
2.m?-6m+9=( )? - 2· ( ) ·( )+( )? =( )?
1. x?+4x+4= ( )? +2·( )·( )+( )? =( )?
x
2
x + 2
a
a 2b
a + 2b
2b
对照 a?±2ab+b?=(a±b)?,填空:
m
m - 3
3
x
2
m
3
下列各式是不是完全平方式?
(1)a2-4a+4; (2)1+4a?;
(3)4b2+4b-1; (4)a2+ab+b2;
(5)x2+x+0.25.
是
(2)因为它只有两项;
不是
(3)4b?与-1的符号不统一;
不是
分析:
不是
是
(4)因为ab不是a与b的积的2倍.
如果x2-6x+N是一个完全平方式,那么N是( )
A . 11 B. 9 C. -11 D. -9
B
解析:根据完全平方式的特征,中间项:
-6x=2x×(-3),故可知N=(-3)2=9.
如果x2-mx+16是一个完全平方式,那么m的值为___.
解析:∵16=(±4)2,故-m=2×(±4),m=±8.
±8
例1
练一练
分解因式:
(1)x2+14x+49; (2)(m+n)2-6(m+n)+9.
分析:(1)中, x2=x2, 49=7?,14x=2·x·7, 所以x2+14x
+49是一个完全平方式,即x2 + 14x +49= x2+ 2·x·7 + 72.
2
a
b
+b2
a2
(2)中,把(m+n)看成一个整体,所以(m+n)2-6(m+n)+9是一个完全平方式.
例2
解: (1)x2++14x +49
= (x + 7)2;
解:原式= x2 + 2·x·7 + 72
(2) (m+n)2-6(m+n)+9
解:原式=[(m+n)-3]2
=(m+n-3)2.
把下列式子分解因式
(1)m2 -12mn+36n2
解:原式=m2-2·m·6n+(6n)2
=(m-6n)2
(2)a2-2a(b+c)+(b+c)2
解:原式=a2-2·a· (b+c) + (b+c) 2
=[a- (b+c) ]2
=(a-b-c)2
把下列各式分解因式:
(1)3ax2+6axy+3ay2 ;(2)-x2-4y2+4xy.
解: (1)原式=3a(x2+2xy+y2)
=3a(x+y)2;
分析:(1)中有公因式3a,应先提出公因式,再进一步分解因式;
(2)中首项有负号,一般先利用添括号法则,将其变形为-(x2-4xy+4y2),然后再利用公式分解因式.
(2)原式=-(x2-4xy+4y2)
=-(x-2y)2.
例3
因式分解:
(1)-3a2x2+24a2x-48a2;
(2)(a2+4)2-16a2.
=(a2+4+4a)(a2+4-4a)
解:(1)原式=-3a2(x2-8x+16)
=-3a2(x-4)2;
(2)原式=(a2+4)2-(4a)2
=(a+2)2(a-2)2.
有公因式要先提公因式
要检查每一个多项式的因式,看能否继续分解.
练一练
(1)形如________________形式的多项式可以用完全平方公式分解因式。
(3)因式分解要_________.
(2)因式分解通常首先考虑______________方法。
提取公因式法
彻底
完全平方公式分解因式
公式
a2±2ab+b2=(a±b)2
特点
(1)要求多项式有三项.
(2)其中两项同号,且都可以写成某数或式的平方,另一项则是这两数或式的乘积的2倍,符号可正可负.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
