北师大版八年级下册数学1.2《直角三角形的性质与判定》课件 (共21张PPT)
文档属性
| 名称 | 北师大版八年级下册数学1.2《直角三角形的性质与判定》课件 (共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 595.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 00:00:00 | ||
图片预览






文档简介
创设情境
2002年国际数学家大会在我国北京召开,大会会徽是根据中国古代数学家赵爽的“弦图”设计的。
第一章 三角形的证明
2.直角三角形(一)
直角三角形有哪些性质?
反之,一个三角形满足什么条件
才能是直角三角形呢?
温故知新
c
a
b
新知讲解
想一想:直角三角形的两个锐角为什么互余呢?
已知:如图(1) 所示,在Rt?ABC中,∠C=90°.
求证: ∠A +∠B=90°.
证明:在Rt?ABC中,
∵∠A +∠B+∠C=90°.
又∵∠C=90°,
∴ ∠A +∠B=90°.
即:直角三角形的两个锐角互余.
A
B
C
(1)
一、我们一起观察直角三角形的角和边,思考它的性质和判定方法。
(一)仅观察角
反之,如果一个三角形有两个角互余,那么这个三角形是直角三角形吗?为什么?
已知:如图(2) 所示,在?ABC中,∠A +∠B=90°.
求证:?ABC是直角三角形
证明:在?ABC中,
∵∠A +∠B+∠C=90°.
又∵∠A +∠B=90°,
∴ ∠C=90°.
∴?ABC是直角三角形.
即:有两个角互余的三角形是直角三角形.
新知讲解
A
B
C
(2)
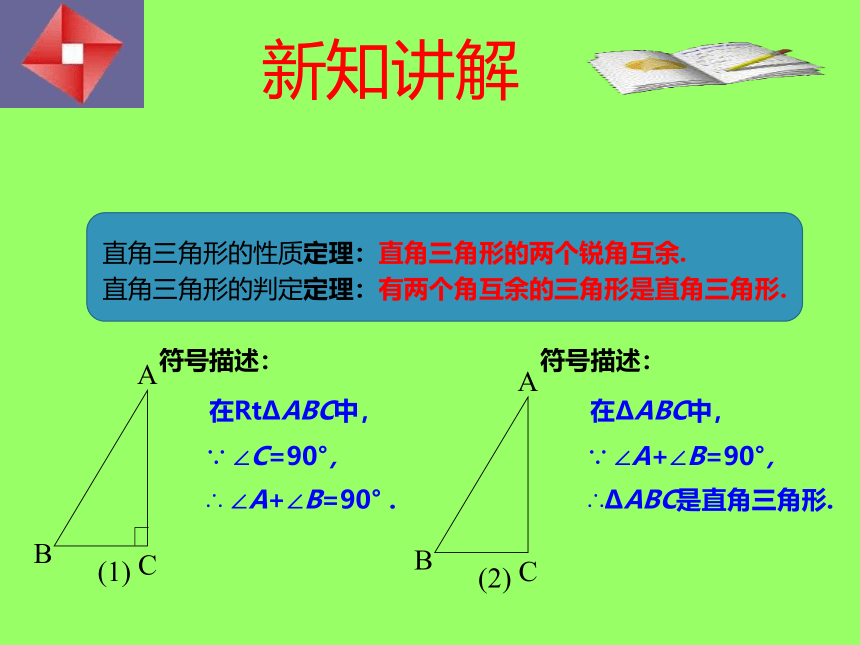
直角三角形的性质定理:直角三角形的两个锐角互余.
直角三角形的判定定理:有两个角互余的三角形是直角三角形.
符号描述:
在Rt?ABC中,
∵ ∠C=90°,
∴ ∠A+∠B=90° .
符号描述:
在?ABC中,
∵ ∠A+∠B=90°,
∴?ABC是直角三角形.
A
B
C
(2)
A
B
C
(1)
新知讲解
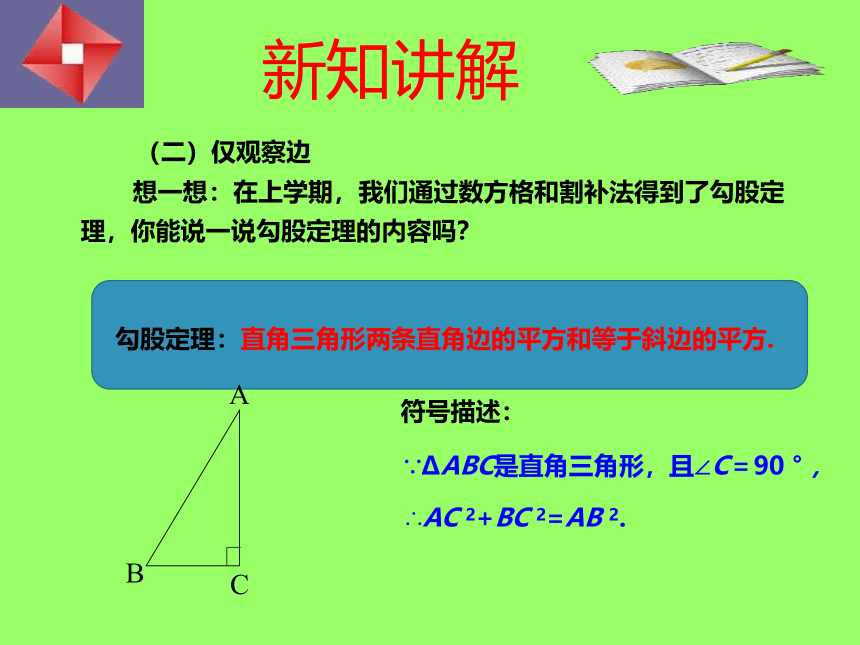
想一想:在上学期,我们通过数方格和割补法得到了勾股定理,你能说一说勾股定理的内容吗?
勾股定理:直角三角形两条直角边的平方和等于斜边的平方.
符号描述:
∵?ABC是直角三角形,且∠C=90 ° ,
∴AC 2+BC 2=AB 2.
(二)仅观察边
新知讲解
A
B
C
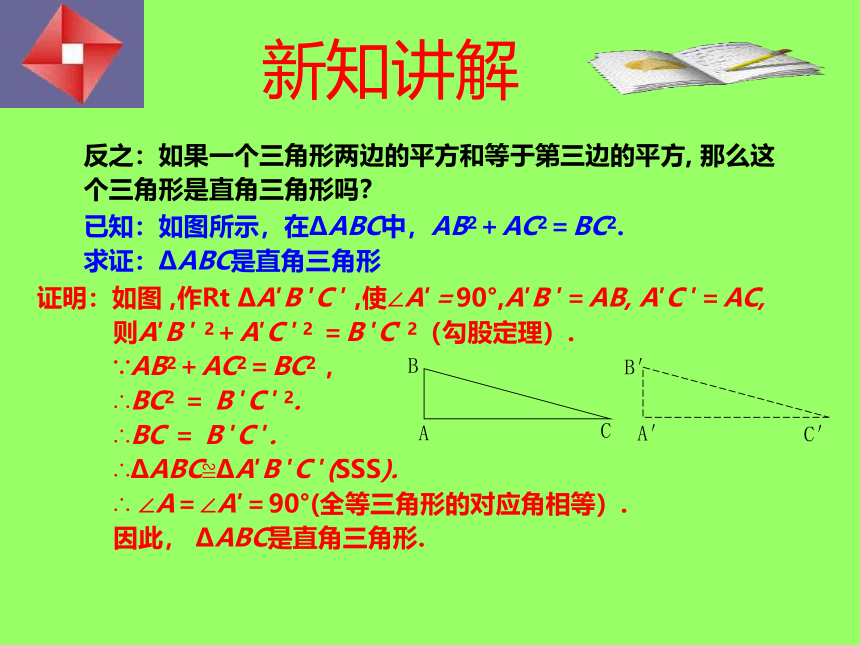
证明:如图 ,作Rt ?A′B ′C ′ ,使∠A′=90°,A′B ′=AB, A′C ′=AC,
则A′B ′ 2+A′C ′ 2 =B ′C′ 2(勾股定理).
∵AB2+AC2=BC2 ,
∴BC2 = B ′C ′ 2.
∴BC = B ′C ′.
∴?ABC≌?A′B ′C ′(SSS).
∴ ∠A=∠A′=90°(全等三角形的对应角相等).
因此, ?ABC是直角三角形.
反之:如果一个三角形两边的平方和等于第三边的平方, 那么这个三角形是直角三角形吗?
已知:如图所示,在?ABC中,AB2+AC2=BC2.
求证:?ABC是直角三角形
新知讲解
B
A
C
C′
A′
B′
直角三角形的判定定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
符号描述:
在?ABC中
∵ AC 2+BC 2=AB 2,
∴ ?ABC是直角三角形.
新知讲解
A
B
C
议一议:观察下面两组定理,它们的条件和结论之间有怎样的关系?
定理:直角三角形的两个锐角互余.
勾股定理:直角三角形两条直角边的平方和等于斜边的平方.
定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
议一议
议一议
定理:有两个角互余的三角形是直角三角形.
条件 结论
条件 结论
再观察下面三组命题:
(1)如果两个角是对顶角,那么它们相等;
如果两个角相等,那么它们是对顶角.
(2)如果小明患了肺炎,那么他一定会发烧;
如果小明发烧,那么他一定患了肺炎.
(3)一个三角形中相等的边所对的角相等;
一个三角形中相等的角所对的边相等.
每组中两个命题的条件和结论也有类似的关系吗?
新知讲解
条件 结论
条件 结论
注:互逆命题是一对命题的称呼,其中一个命题称原命题,另一个命题称原命题的逆命题.
你能写出命题“如果两个有理数相等,那么它们的平方相等”的逆命题吗?
如果两个有理数的平方相等,那么这两个有理数相等.
它们都是真命题吗?
第一个命题是真命题,它的逆命题是假命题.
注意:一个命题是真命题,它的逆命题不一定是真命题.判断一个命题是真命题需要进行逻辑推理,判断一个命题是假命题只需要举反例就可以.
新知讲解
在两个命题中,如果一个命题的条件和结论分别 是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题.
一、互逆命题、逆命题的定义
二、命题一定是真命题吗?
如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,其中一个定理称为另一个定理的逆定理,这两个定理称为互逆定理.
定理:直角三角形的两个锐角互余.
定理:有两个角互余的三角形是直角三角形.
互逆定理
新知讲解
互逆定理
勾股定理:直角三角形两条直角边的平方和等于斜边的平方.
定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
议一议:你还能想到其它互逆定理吗?
练一练
′
例1:说出下列命题的逆命题,并判断每对命题的真假?
四边形是多边形;
直角三角形有一个角是直角;
两直线平行,同旁内角互补;
如果ab=0,那么a=0,b=0.
游戏1:请甲同学说出一个命题,乙同学回答出它的逆命题,并判断这个逆命题的真假.若乙同学回答的逆命题和真假都正确,则乙胜,否则甲胜。轮流各出两次题,决出最终胜者。
读一读
2、中国古代的数学家们不仅很早就发现并应用勾股定理,而且很早就尝试对勾股定理作理论的证明。最早对勾股定理进行证明的,是三国时期吴国的数学家赵爽。赵爽创制了一幅“勾股圆方图”,用形数结合的方法,给出了勾股定理的详细证明。
勾股定理的证明
1、请阅读教材P16勾股定理的证明材料,读完后与同伴交流证明过程中使用了哪些数学方法,并相互合作探究其他证明方法。
c
a
(弦)c
(勾)a
c
(股) b
c
a
∵ c2= 4?ab/2 +(b-a)2
c2 =2ab+b2-2ab+a2
c2 =a2+b2
∴a2+b2=c2
赵爽创制的“勾股圆方图”如图:
大正方形的面积可以表示为 ;
c2
4?ab/2+(b- a)2
赵爽的证法如下:
也可以用4个直角三角形和中间小正方形的面积之和表示为
解:(1)中间的小正方形边长可表示为b-a,当b-a=0,即b=a时,中间的小正方形面积最小。
知识拓展:
赵爽创制的“勾股圆方图”如图:请探究:
(1)勾a,股b满足什么关系时?中间的小正方形面积最小。
(2)当勾a对应的锐角为30°时,此图最和谐美丽,请问此时大正方形的面积和中间小正方形的面积有何关系?
A
c
a
(弦)c
(勾)a
c
(股) b
c
a
B
C
(2)当勾a对应的锐角为30°时,此图最和谐美丽,请问此时大正方形的面积和中间小正方形的面积有何关系?
A
c
a
(弦)c
(勾)a
c
(股) b
c
a
B
C
解:在Rt△ABC中,∠CAB=30°,BC=a,
∴AB=2BC=2a.
∴AC2=AB2-BC2=4a2-a2=3a2, 既AC=????a
?
∵大正方形的面积为:S大=c2= (2a)2=4a2,
小正方形的面积为:
S小= (b-a)2= (????a-a)2= (????-1)2a2=2?????2?4a2
?
∴S小=2?????2 S大
?
知识拓展:
1、说一说直角三角形在角上的性质与判定?
性质:直角三角形的两个锐角互余.
判定:有两个角互余的三角形是直角三角形.
2、说一说直角三角形在边上的性质与判定?
勾股定理(性质):直角三角形两条直角边的平方和等于斜边的平方.
勾股定理的逆定理(判定):如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
我会总结:
3、什么是互逆命题、互逆定理?
在两个命题中,如果一个命题的条件和结论分别 是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题.
如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,其中一个定理称为另一个定理的逆定理,这两个定理称为互逆定理.
我会总结:
1、家庭作业
教科书习题1.5
2、调查研究
利用课余时间,去调查勾股定理在生活中的运用,并写出简要的调查过程和结论。
我的作业
2002年国际数学家大会在我国北京召开,大会会徽是根据中国古代数学家赵爽的“弦图”设计的。
第一章 三角形的证明
2.直角三角形(一)
直角三角形有哪些性质?
反之,一个三角形满足什么条件
才能是直角三角形呢?
温故知新
c
a
b
新知讲解
想一想:直角三角形的两个锐角为什么互余呢?
已知:如图(1) 所示,在Rt?ABC中,∠C=90°.
求证: ∠A +∠B=90°.
证明:在Rt?ABC中,
∵∠A +∠B+∠C=90°.
又∵∠C=90°,
∴ ∠A +∠B=90°.
即:直角三角形的两个锐角互余.
A
B
C
(1)
一、我们一起观察直角三角形的角和边,思考它的性质和判定方法。
(一)仅观察角
反之,如果一个三角形有两个角互余,那么这个三角形是直角三角形吗?为什么?
已知:如图(2) 所示,在?ABC中,∠A +∠B=90°.
求证:?ABC是直角三角形
证明:在?ABC中,
∵∠A +∠B+∠C=90°.
又∵∠A +∠B=90°,
∴ ∠C=90°.
∴?ABC是直角三角形.
即:有两个角互余的三角形是直角三角形.
新知讲解
A
B
C
(2)
直角三角形的性质定理:直角三角形的两个锐角互余.
直角三角形的判定定理:有两个角互余的三角形是直角三角形.
符号描述:
在Rt?ABC中,
∵ ∠C=90°,
∴ ∠A+∠B=90° .
符号描述:
在?ABC中,
∵ ∠A+∠B=90°,
∴?ABC是直角三角形.
A
B
C
(2)
A
B
C
(1)
新知讲解
想一想:在上学期,我们通过数方格和割补法得到了勾股定理,你能说一说勾股定理的内容吗?
勾股定理:直角三角形两条直角边的平方和等于斜边的平方.
符号描述:
∵?ABC是直角三角形,且∠C=90 ° ,
∴AC 2+BC 2=AB 2.
(二)仅观察边
新知讲解
A
B
C
证明:如图 ,作Rt ?A′B ′C ′ ,使∠A′=90°,A′B ′=AB, A′C ′=AC,
则A′B ′ 2+A′C ′ 2 =B ′C′ 2(勾股定理).
∵AB2+AC2=BC2 ,
∴BC2 = B ′C ′ 2.
∴BC = B ′C ′.
∴?ABC≌?A′B ′C ′(SSS).
∴ ∠A=∠A′=90°(全等三角形的对应角相等).
因此, ?ABC是直角三角形.
反之:如果一个三角形两边的平方和等于第三边的平方, 那么这个三角形是直角三角形吗?
已知:如图所示,在?ABC中,AB2+AC2=BC2.
求证:?ABC是直角三角形
新知讲解
B
A
C
C′
A′
B′
直角三角形的判定定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
符号描述:
在?ABC中
∵ AC 2+BC 2=AB 2,
∴ ?ABC是直角三角形.
新知讲解
A
B
C
议一议:观察下面两组定理,它们的条件和结论之间有怎样的关系?
定理:直角三角形的两个锐角互余.
勾股定理:直角三角形两条直角边的平方和等于斜边的平方.
定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
议一议
议一议
定理:有两个角互余的三角形是直角三角形.
条件 结论
条件 结论
再观察下面三组命题:
(1)如果两个角是对顶角,那么它们相等;
如果两个角相等,那么它们是对顶角.
(2)如果小明患了肺炎,那么他一定会发烧;
如果小明发烧,那么他一定患了肺炎.
(3)一个三角形中相等的边所对的角相等;
一个三角形中相等的角所对的边相等.
每组中两个命题的条件和结论也有类似的关系吗?
新知讲解
条件 结论
条件 结论
注:互逆命题是一对命题的称呼,其中一个命题称原命题,另一个命题称原命题的逆命题.
你能写出命题“如果两个有理数相等,那么它们的平方相等”的逆命题吗?
如果两个有理数的平方相等,那么这两个有理数相等.
它们都是真命题吗?
第一个命题是真命题,它的逆命题是假命题.
注意:一个命题是真命题,它的逆命题不一定是真命题.判断一个命题是真命题需要进行逻辑推理,判断一个命题是假命题只需要举反例就可以.
新知讲解
在两个命题中,如果一个命题的条件和结论分别 是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题.
一、互逆命题、逆命题的定义
二、命题一定是真命题吗?
如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,其中一个定理称为另一个定理的逆定理,这两个定理称为互逆定理.
定理:直角三角形的两个锐角互余.
定理:有两个角互余的三角形是直角三角形.
互逆定理
新知讲解
互逆定理
勾股定理:直角三角形两条直角边的平方和等于斜边的平方.
定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
议一议:你还能想到其它互逆定理吗?
练一练
′
例1:说出下列命题的逆命题,并判断每对命题的真假?
四边形是多边形;
直角三角形有一个角是直角;
两直线平行,同旁内角互补;
如果ab=0,那么a=0,b=0.
游戏1:请甲同学说出一个命题,乙同学回答出它的逆命题,并判断这个逆命题的真假.若乙同学回答的逆命题和真假都正确,则乙胜,否则甲胜。轮流各出两次题,决出最终胜者。
读一读
2、中国古代的数学家们不仅很早就发现并应用勾股定理,而且很早就尝试对勾股定理作理论的证明。最早对勾股定理进行证明的,是三国时期吴国的数学家赵爽。赵爽创制了一幅“勾股圆方图”,用形数结合的方法,给出了勾股定理的详细证明。
勾股定理的证明
1、请阅读教材P16勾股定理的证明材料,读完后与同伴交流证明过程中使用了哪些数学方法,并相互合作探究其他证明方法。
c
a
(弦)c
(勾)a
c
(股) b
c
a
∵ c2= 4?ab/2 +(b-a)2
c2 =2ab+b2-2ab+a2
c2 =a2+b2
∴a2+b2=c2
赵爽创制的“勾股圆方图”如图:
大正方形的面积可以表示为 ;
c2
4?ab/2+(b- a)2
赵爽的证法如下:
也可以用4个直角三角形和中间小正方形的面积之和表示为
解:(1)中间的小正方形边长可表示为b-a,当b-a=0,即b=a时,中间的小正方形面积最小。
知识拓展:
赵爽创制的“勾股圆方图”如图:请探究:
(1)勾a,股b满足什么关系时?中间的小正方形面积最小。
(2)当勾a对应的锐角为30°时,此图最和谐美丽,请问此时大正方形的面积和中间小正方形的面积有何关系?
A
c
a
(弦)c
(勾)a
c
(股) b
c
a
B
C
(2)当勾a对应的锐角为30°时,此图最和谐美丽,请问此时大正方形的面积和中间小正方形的面积有何关系?
A
c
a
(弦)c
(勾)a
c
(股) b
c
a
B
C
解:在Rt△ABC中,∠CAB=30°,BC=a,
∴AB=2BC=2a.
∴AC2=AB2-BC2=4a2-a2=3a2, 既AC=????a
?
∵大正方形的面积为:S大=c2= (2a)2=4a2,
小正方形的面积为:
S小= (b-a)2= (????a-a)2= (????-1)2a2=2?????2?4a2
?
∴S小=2?????2 S大
?
知识拓展:
1、说一说直角三角形在角上的性质与判定?
性质:直角三角形的两个锐角互余.
判定:有两个角互余的三角形是直角三角形.
2、说一说直角三角形在边上的性质与判定?
勾股定理(性质):直角三角形两条直角边的平方和等于斜边的平方.
勾股定理的逆定理(判定):如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
我会总结:
3、什么是互逆命题、互逆定理?
在两个命题中,如果一个命题的条件和结论分别 是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题.
如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,其中一个定理称为另一个定理的逆定理,这两个定理称为互逆定理.
我会总结:
1、家庭作业
教科书习题1.5
2、调查研究
利用课余时间,去调查勾股定理在生活中的运用,并写出简要的调查过程和结论。
我的作业
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
