北师大版九年级数学下册3.3:垂径定理 课件(共20张PPT)
文档属性
| 名称 | 北师大版九年级数学下册3.3:垂径定理 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 474.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 00:00:00 | ||
图片预览





文档简介
第三章 圆
第3节 垂径定理
学习目标
一、 了解垂径定理的内涵
二、 熟悉垂径定理的推论
基础回顾
1.等腰三角形是轴对称图形吗?
2.如果将一等腰三角形沿底边上的高对折,可以发现什么结论?
3.如果以这个等腰三角形的顶角顶点为圆心,腰长为半径画圆,得到的图形是否是轴对称图形呢?
知识点1
垂径定理
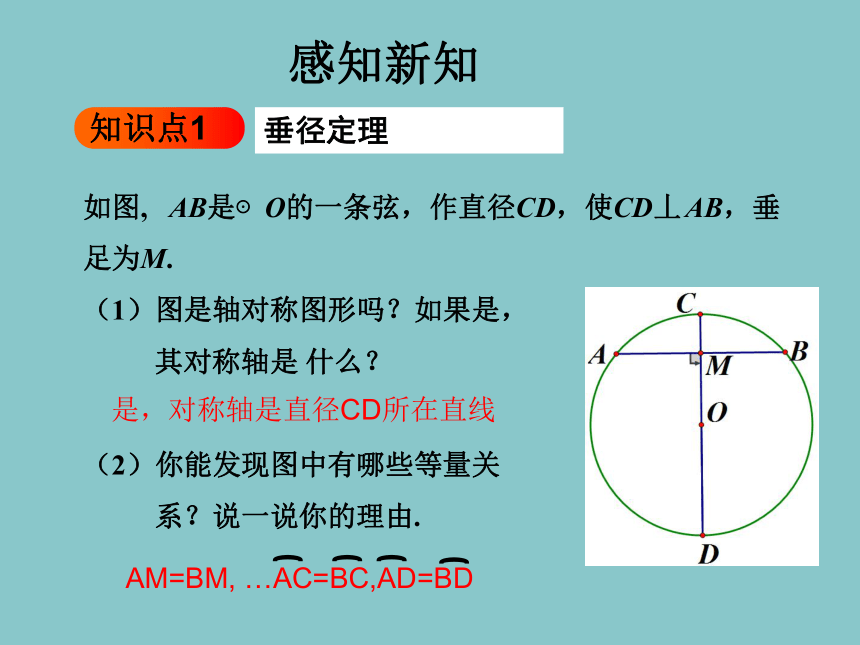
如图, AB是⊙O的一条弦,作直径CD,使CD丄 AB,垂
足为M.
(1)图是轴对称图形吗?如果是,
其对称轴是 什么?
(2)你能发现图中有哪些等量关
系?说一说你的理由.
感知新知
是,对称轴是直径CD所在直线
AM=BM, …AC=BC,AD=BD
定理推导
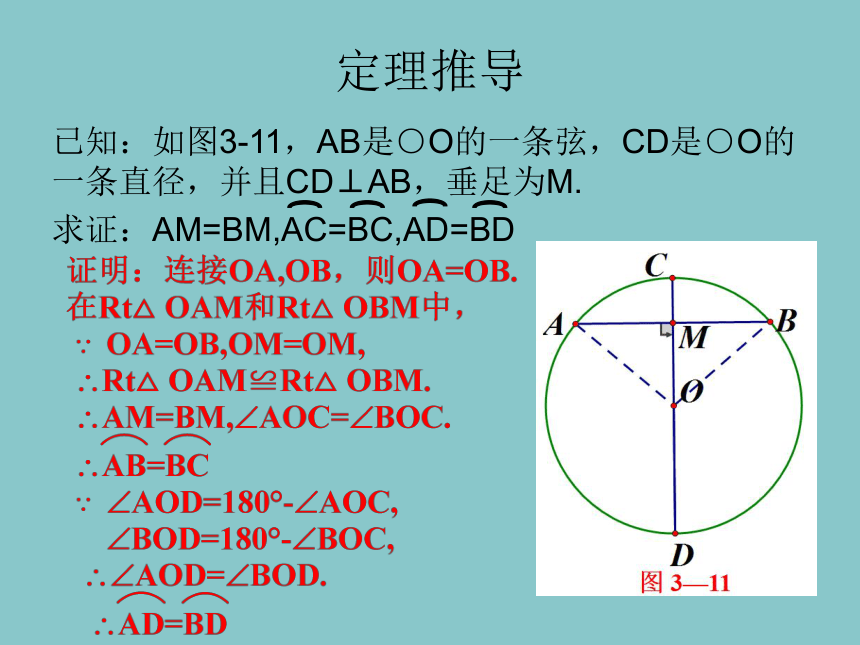
已知:如图3-11,AB是○O的一条弦,CD是○O的一条直径,并且CD⊥AB,垂足为M.
求证:AM=BM,AC=BC,AD=BD
定理总结
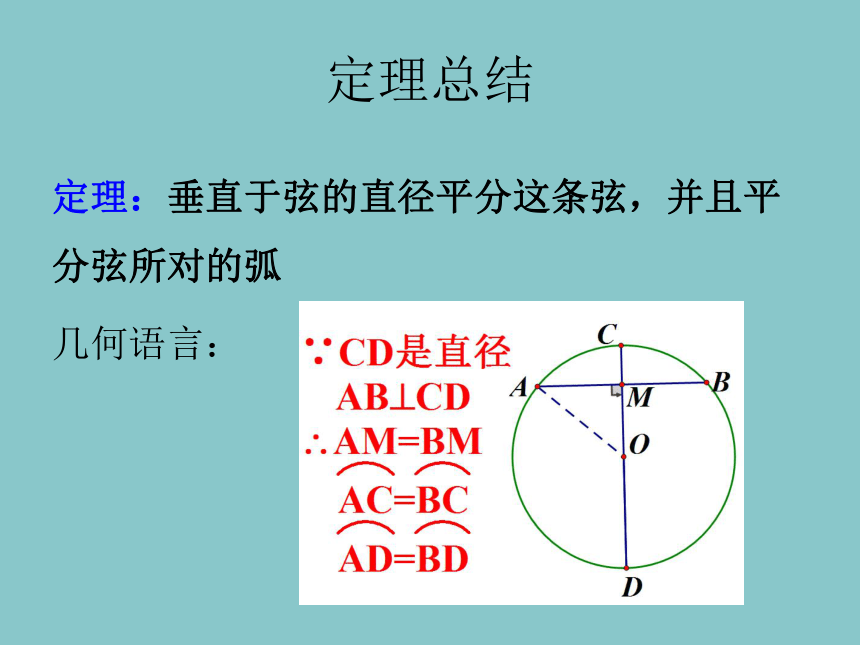
定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧
几何语言:
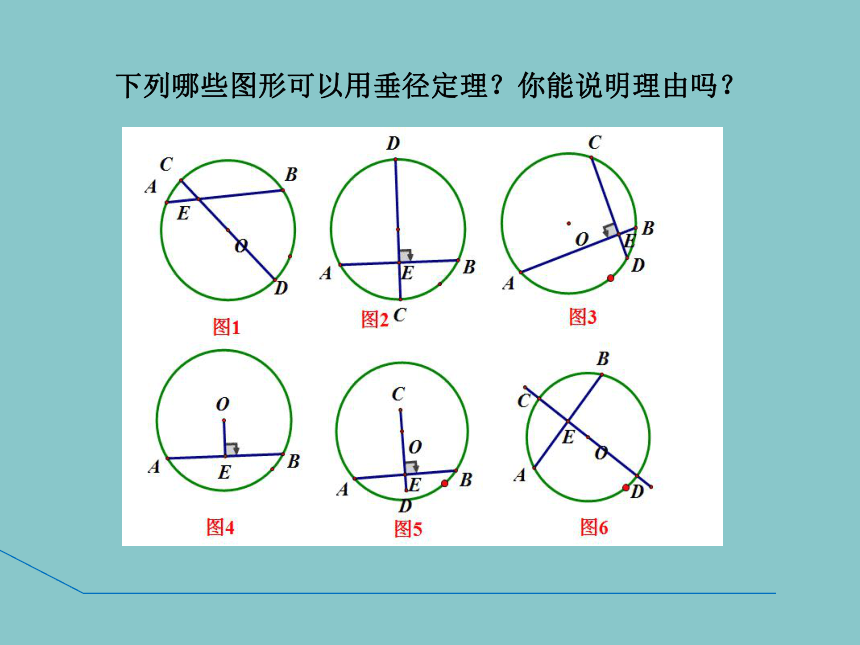
下列哪些图形可以用垂径定理?你能说明理由吗?
如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=12,BE=2,则⊙O的直径为( )
A.8 B.10
C.16 D.20
例1
导引:
连接OC.根据垂径定理,知CE= CD=6.在Rt△OEC
中,设OC=x,由BE=2,得OE=x-2.所以(x-2)2+62
=x2,解得x=10,即直径AB=20.
D
1400年前,我国隋朝建造的赵州石拱桥(如图)是圆弧形,它的跨度(即弧所 对的弦长)为37.4 m,拱高(即弧的中点到弦的距离)为7.2 m,求桥拱所在圆的半径(结果精确到0.1).
1
解:
如图,∵OD⊥AB,
∴AD= AB= ×37.4=18.7(m).
在Rt△ODA中,
OD=(R-7.2) m,OA=R m,
∴R2=(R-7.2)2+18.72,
解得R≈27.9.
∴桥拱所在圆的半径约为27.9 m.
2
知识点
垂径定理的推论
如图, AB是⊙O的弦(不是直径),作一条平分AB的直
径CD), 交AB于点M.
(1)图是轴对称图形吗?如果是,
其对称轴是什么?
(2)你能发现图中有哪些等量关系?说一说你的理由.
是,对称轴是CD所在直线
已知:如图3-12,AB是○O的一条弦(不是直径),CD是○O的一条直径,AB与CD相交于点M,并且AM=BM,.
求证:
平分弦(不是直径)的直径垂直于弦,并且平分
弦所对的弧.
定理小结
思考:为什么有括号内的限制?
下列说法正确的是( )
A.经过弦的中点的直线平分弦所对的弧
B.过弦的中点的直线一定经过圆心
C.弦所对的两条弧的中点的连线垂直平分弦且经
过圆心
D.弦的垂线平分弦所对的弧
1.
C
2.如图,⊙O的直径CD=20 cm,AB是⊙O的弦,AM
=BM,OM∶MC=3∶2,则AB的长为( )
A.18 cm
cm
C.16cm
D.22 cm
C
3.如图,△ABC的三个顶点都在⊙O上,∠AOB=60°,AB=AC=2,则弦BC的长为( )
A.
B.3
C.2
D.4
C
4.【中考】如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,她了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25 m,BD=1.5 m,且AB,CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )
A.2 m
B.2.5 m
C.2.4 m
D.2.1
B
5.如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗?为什么?
O
C
D
B
A
O
C
D
B
A
O
C
D
B
A
有三种情况:1、圆心在平行弦外;
2、圆心在其中一条弦上;
3、圆心在平行弦内.
垂径定理:
(1)垂径定理 垂直于弦的直径平分这条弦,并且平分
弦所对的弧.
本节课我们学了什么?
(2)垂径定理的推论:平分弦(不是直径)的直径垂直于弦,
并且平分弦所对的弧.
关于垂径定理及其推论可归纳为:一条直线,它具
备以下五个性质:
①直线过圆心;
②直线垂直于弦;
③直线平分弦(不是直径);
④直线平分弦所对的优弧;
⑤直线平分弦所对的劣弧.如果把其中的任意两条作为
条件,其余三条作为结论,组成的命题都是真命题.
以上说法正确吗,课后自己去试试?
第3节 垂径定理
学习目标
一、 了解垂径定理的内涵
二、 熟悉垂径定理的推论
基础回顾
1.等腰三角形是轴对称图形吗?
2.如果将一等腰三角形沿底边上的高对折,可以发现什么结论?
3.如果以这个等腰三角形的顶角顶点为圆心,腰长为半径画圆,得到的图形是否是轴对称图形呢?
知识点1
垂径定理
如图, AB是⊙O的一条弦,作直径CD,使CD丄 AB,垂
足为M.
(1)图是轴对称图形吗?如果是,
其对称轴是 什么?
(2)你能发现图中有哪些等量关
系?说一说你的理由.
感知新知
是,对称轴是直径CD所在直线
AM=BM, …AC=BC,AD=BD
定理推导
已知:如图3-11,AB是○O的一条弦,CD是○O的一条直径,并且CD⊥AB,垂足为M.
求证:AM=BM,AC=BC,AD=BD
定理总结
定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧
几何语言:
下列哪些图形可以用垂径定理?你能说明理由吗?
如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=12,BE=2,则⊙O的直径为( )
A.8 B.10
C.16 D.20
例1
导引:
连接OC.根据垂径定理,知CE= CD=6.在Rt△OEC
中,设OC=x,由BE=2,得OE=x-2.所以(x-2)2+62
=x2,解得x=10,即直径AB=20.
D
1400年前,我国隋朝建造的赵州石拱桥(如图)是圆弧形,它的跨度(即弧所 对的弦长)为37.4 m,拱高(即弧的中点到弦的距离)为7.2 m,求桥拱所在圆的半径(结果精确到0.1).
1
解:
如图,∵OD⊥AB,
∴AD= AB= ×37.4=18.7(m).
在Rt△ODA中,
OD=(R-7.2) m,OA=R m,
∴R2=(R-7.2)2+18.72,
解得R≈27.9.
∴桥拱所在圆的半径约为27.9 m.
2
知识点
垂径定理的推论
如图, AB是⊙O的弦(不是直径),作一条平分AB的直
径CD), 交AB于点M.
(1)图是轴对称图形吗?如果是,
其对称轴是什么?
(2)你能发现图中有哪些等量关系?说一说你的理由.
是,对称轴是CD所在直线
已知:如图3-12,AB是○O的一条弦(不是直径),CD是○O的一条直径,AB与CD相交于点M,并且AM=BM,.
求证:
平分弦(不是直径)的直径垂直于弦,并且平分
弦所对的弧.
定理小结
思考:为什么有括号内的限制?
下列说法正确的是( )
A.经过弦的中点的直线平分弦所对的弧
B.过弦的中点的直线一定经过圆心
C.弦所对的两条弧的中点的连线垂直平分弦且经
过圆心
D.弦的垂线平分弦所对的弧
1.
C
2.如图,⊙O的直径CD=20 cm,AB是⊙O的弦,AM
=BM,OM∶MC=3∶2,则AB的长为( )
A.18 cm
cm
C.16cm
D.22 cm
C
3.如图,△ABC的三个顶点都在⊙O上,∠AOB=60°,AB=AC=2,则弦BC的长为( )
A.
B.3
C.2
D.4
C
4.【中考】如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,她了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25 m,BD=1.5 m,且AB,CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )
A.2 m
B.2.5 m
C.2.4 m
D.2.1
B
5.如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗?为什么?
O
C
D
B
A
O
C
D
B
A
O
C
D
B
A
有三种情况:1、圆心在平行弦外;
2、圆心在其中一条弦上;
3、圆心在平行弦内.
垂径定理:
(1)垂径定理 垂直于弦的直径平分这条弦,并且平分
弦所对的弧.
本节课我们学了什么?
(2)垂径定理的推论:平分弦(不是直径)的直径垂直于弦,
并且平分弦所对的弧.
关于垂径定理及其推论可归纳为:一条直线,它具
备以下五个性质:
①直线过圆心;
②直线垂直于弦;
③直线平分弦(不是直径);
④直线平分弦所对的优弧;
⑤直线平分弦所对的劣弧.如果把其中的任意两条作为
条件,其余三条作为结论,组成的命题都是真命题.
以上说法正确吗,课后自己去试试?
