北师大版九年级数学下册3.6: 第1课时 直线和圆的位置关系及切线的性质 课件(共16张PPT)
文档属性
| 名称 | 北师大版九年级数学下册3.6: 第1课时 直线和圆的位置关系及切线的性质 课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 866.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 12:23:21 | ||
图片预览



文档简介
第三章 圆
3.6 直线和圆的位置关系
第1课时 直线和圆的位置关系及切线的性质
1.理解直线与圆有三种位置关系,并能利用公共点的个数,圆心到直线的距离与半径之间的关系来判定它们.
2.掌握直线与圆相切的判断方法和如何作出直线与圆相切,并能利用公共点的个数和圆心到直线的距离与半径之间的关系来判定.
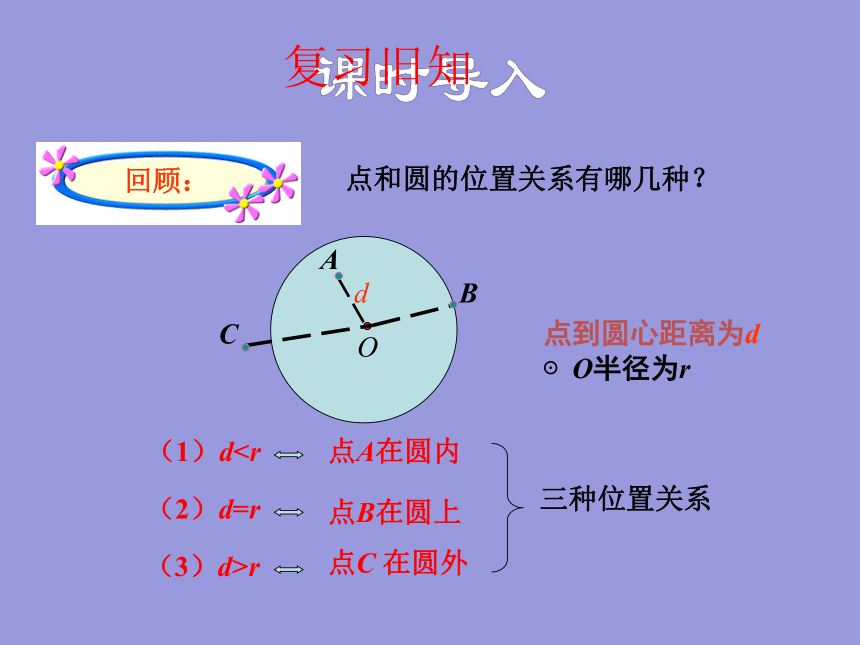
点和圆的位置关系有哪几种?
(1)d(2)d=r
(3)d>r
A
B
C
d
点A在圆内
点B在圆上
点C 在圆外
三种位置关系
O
点到圆心距离为d
⊙O半径为r
回顾:
复习旧知
太阳与地平线、乒乓球与球拍的图片给你留下了_________ 的位置关系的印象.
直线与圆
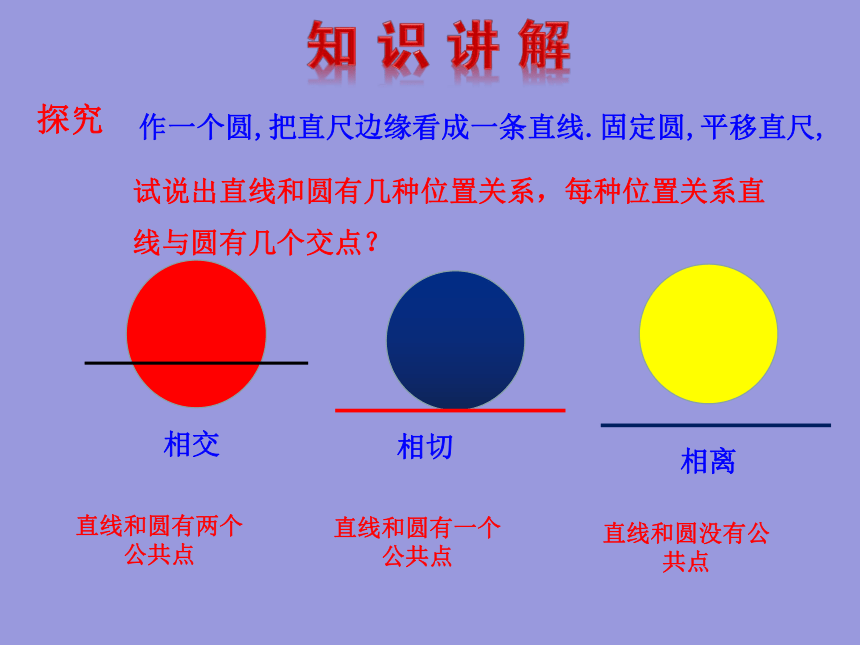
作一个圆,把直尺边缘看成一条直线.固定圆,平移直尺,
相交
相切
相离
直线和圆有两个公共点
直线和圆有一个公共点
直线和圆没有公共点
探究
试说出直线和圆有几种位置关系,每种位置关系直线与圆有几个交点?
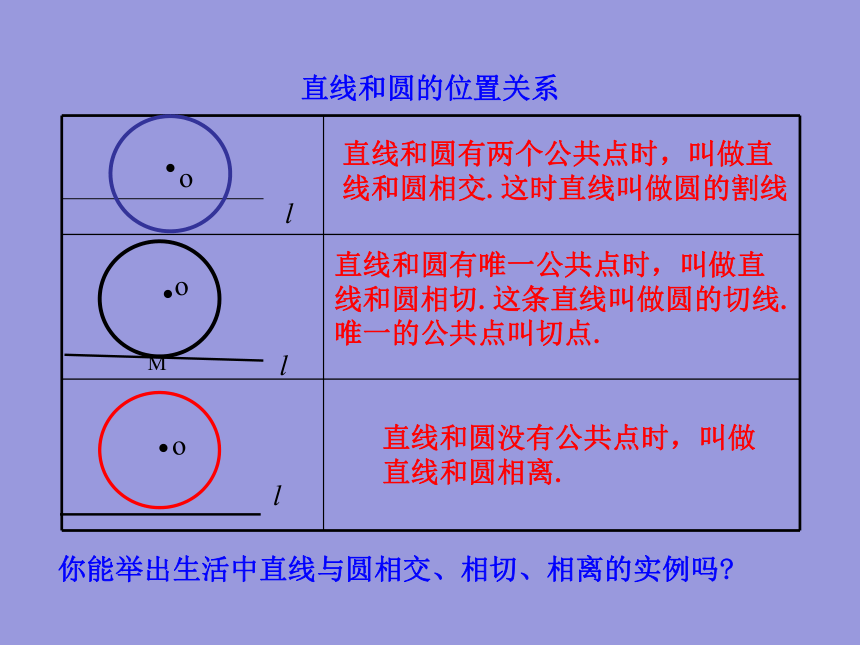
直线和圆的位置关系
l
l
l
?
?
?
直线和圆有两个公共点时,叫做直线和圆相交.这时直线叫做圆的割线
直线和圆有唯一公共点时,叫做直线和圆相切.这条直线叫做圆的切线.唯一的公共点叫切点.
直线和圆没有公共点时,叫做直线和圆相离.
o
o
o
M
你能举出生活中直线与圆相交、相切、相离的实例吗?
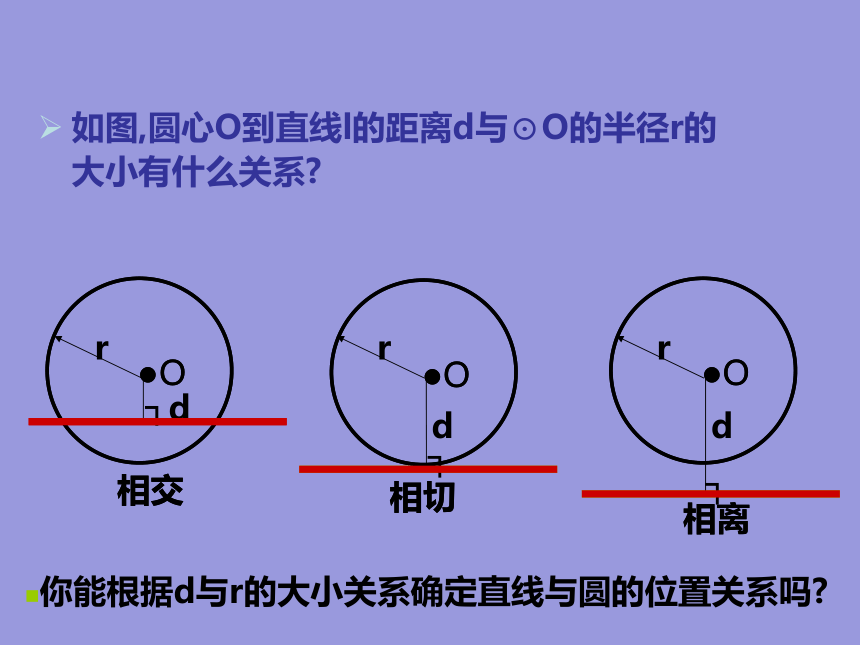
如图,圆心O到直线l的距离d与⊙O的半径r的大小有什么关系?
你能根据d与r的大小关系确定直线与圆的位置关系吗?
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
●O
●O
相交
●O
相切
相离
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
1)直线和圆相交
d______r;
2) 直线和圆相切
3) 直线和圆相离
<
d______r;
=
d______r;
>
【中考】在平面直角坐标系中,以点(5,6)为圆心、5为半径的圆,一定( )
A.与x轴相切,与y轴相切 B.与x轴相切,与y轴相交
C.与x轴相离,与y轴相切 D.与x轴相交,与y轴相交
C
及时巩固
【中考】在Rt△ABC中,∠C=90°,BC=3 cm,AC=4 cm,以点C为圆心,以2.3 cm为半径画圆,则⊙C与直线AB的位置关系是( )
A.相交 B.相切
C.相离 D.不能确定
c
【中考】已知⊙O的半径为5,N为直线AB上一点,若NO=5,则直线AB与⊙O的位置关系为( )
A.相切 B.相交
C.相切或相离 D.相切或相交
D
探索切线的性质
小松的理由是:直径AB与直线CD要么垂直,要么不垂直.
假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M,
老师期望:
你能看明白(或掌握)用反证法说理的过程.
则OM的半径,因此,CD与⊙O相交.这与已知条件“直
线与⊙O相切”相矛盾.
C
D
B
●O
A
所以AB与CD垂直.
M
切线的性质
参考小松的说理过程,请你写出这个命题:
圆的切线垂直于过切点的半径。
老师提示:
切线的性质是证明两线垂直的重要根据;作过切点的半径是常用的辅助线之一.
如图
∵CD是⊙O的切线,A是切点,OA是⊙O的半径,
∴CD⊥OA.
C
D
B
●O
A
【中考】如图,AB是⊙O的直径,AC切⊙O于点A,BC交⊙O于点D,若∠C=80°,则∠BOD的度数为( )
A.160°
B.155°
C.150°
D.140°
A
牛刀小试,链接中考
【中考】如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,∠A=26°,过点C作⊙O的切线,交AB的延长线于点D,则∠D的度数是( )
A.38°
B.40°
C.42°
D.36°
A
【中考】如图,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的大小是( )
A.15°
B.30°
C.60°
D.75°
B
1.直线和圆的位置关系:相交、相切、相离.
(1)从公共点数来判断;
(2)从d与r间的数量关系来判断.
2.直线和圆的位置关系的性质与判定:
(1)直线和圆相离 d>r;
(2)直线和圆相切 d=r;
(3)直线和圆相交 d<r.
1
知识小结
及时总结
3.6 直线和圆的位置关系
第1课时 直线和圆的位置关系及切线的性质
1.理解直线与圆有三种位置关系,并能利用公共点的个数,圆心到直线的距离与半径之间的关系来判定它们.
2.掌握直线与圆相切的判断方法和如何作出直线与圆相切,并能利用公共点的个数和圆心到直线的距离与半径之间的关系来判定.
点和圆的位置关系有哪几种?
(1)d
(3)d>r
A
B
C
d
点A在圆内
点B在圆上
点C 在圆外
三种位置关系
O
点到圆心距离为d
⊙O半径为r
回顾:
复习旧知
太阳与地平线、乒乓球与球拍的图片给你留下了_________ 的位置关系的印象.
直线与圆
作一个圆,把直尺边缘看成一条直线.固定圆,平移直尺,
相交
相切
相离
直线和圆有两个公共点
直线和圆有一个公共点
直线和圆没有公共点
探究
试说出直线和圆有几种位置关系,每种位置关系直线与圆有几个交点?
直线和圆的位置关系
l
l
l
?
?
?
直线和圆有两个公共点时,叫做直线和圆相交.这时直线叫做圆的割线
直线和圆有唯一公共点时,叫做直线和圆相切.这条直线叫做圆的切线.唯一的公共点叫切点.
直线和圆没有公共点时,叫做直线和圆相离.
o
o
o
M
你能举出生活中直线与圆相交、相切、相离的实例吗?
如图,圆心O到直线l的距离d与⊙O的半径r的大小有什么关系?
你能根据d与r的大小关系确定直线与圆的位置关系吗?
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
●O
●O
相交
●O
相切
相离
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
1)直线和圆相交
d______r;
2) 直线和圆相切
3) 直线和圆相离
<
d______r;
=
d______r;
>
【中考】在平面直角坐标系中,以点(5,6)为圆心、5为半径的圆,一定( )
A.与x轴相切,与y轴相切 B.与x轴相切,与y轴相交
C.与x轴相离,与y轴相切 D.与x轴相交,与y轴相交
C
及时巩固
【中考】在Rt△ABC中,∠C=90°,BC=3 cm,AC=4 cm,以点C为圆心,以2.3 cm为半径画圆,则⊙C与直线AB的位置关系是( )
A.相交 B.相切
C.相离 D.不能确定
c
【中考】已知⊙O的半径为5,N为直线AB上一点,若NO=5,则直线AB与⊙O的位置关系为( )
A.相切 B.相交
C.相切或相离 D.相切或相交
D
探索切线的性质
小松的理由是:直径AB与直线CD要么垂直,要么不垂直.
假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M,
老师期望:
你能看明白(或掌握)用反证法说理的过程.
则OM
线与⊙O相切”相矛盾.
C
D
B
●O
A
所以AB与CD垂直.
M
切线的性质
参考小松的说理过程,请你写出这个命题:
圆的切线垂直于过切点的半径。
老师提示:
切线的性质是证明两线垂直的重要根据;作过切点的半径是常用的辅助线之一.
如图
∵CD是⊙O的切线,A是切点,OA是⊙O的半径,
∴CD⊥OA.
C
D
B
●O
A
【中考】如图,AB是⊙O的直径,AC切⊙O于点A,BC交⊙O于点D,若∠C=80°,则∠BOD的度数为( )
A.160°
B.155°
C.150°
D.140°
A
牛刀小试,链接中考
【中考】如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,∠A=26°,过点C作⊙O的切线,交AB的延长线于点D,则∠D的度数是( )
A.38°
B.40°
C.42°
D.36°
A
【中考】如图,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的大小是( )
A.15°
B.30°
C.60°
D.75°
B
1.直线和圆的位置关系:相交、相切、相离.
(1)从公共点数来判断;
(2)从d与r间的数量关系来判断.
2.直线和圆的位置关系的性质与判定:
(1)直线和圆相离 d>r;
(2)直线和圆相切 d=r;
(3)直线和圆相交 d<r.
1
知识小结
及时总结
