北师大版九年级数学下册3.6:直线和圆的位置关系 2 : 切线的判定定理 课件(共18张PPT)
文档属性
| 名称 | 北师大版九年级数学下册3.6:直线和圆的位置关系 2 : 切线的判定定理 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 466.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 00:00:00 | ||
图片预览




文档简介
3.6 直线和圆的位置关系
第2课时 切线的判定
学习目标
一、圆的切线的判定定理。
二、三角形内切圆的概念与不同三角形
内切圆的特点。
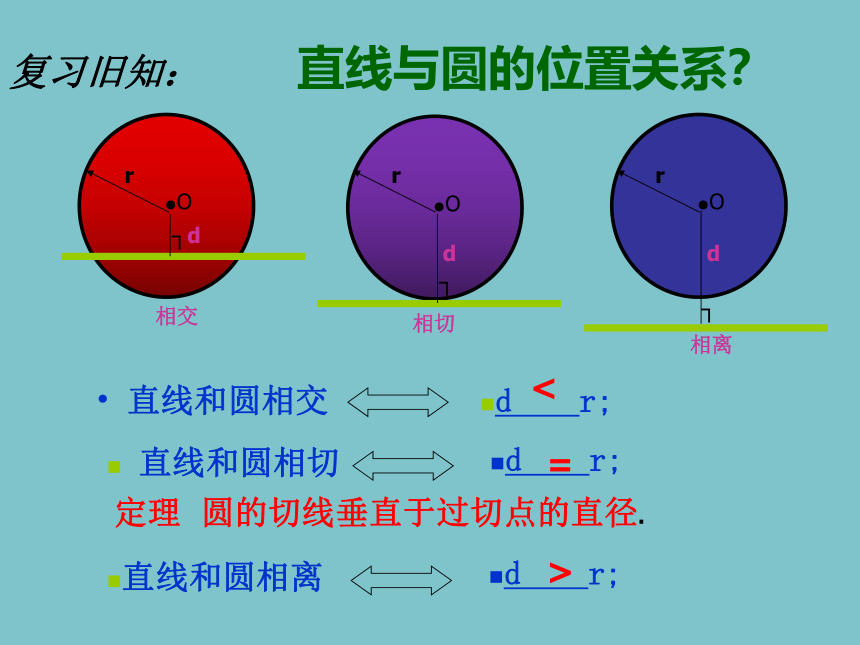
直线和圆相交
d r;
d r;
直线和圆相切
直线和圆相离
d r;
直线与圆的位置关系?
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
<
=
>
复习旧知:
定理 圆的切线垂直于过切点的直径.
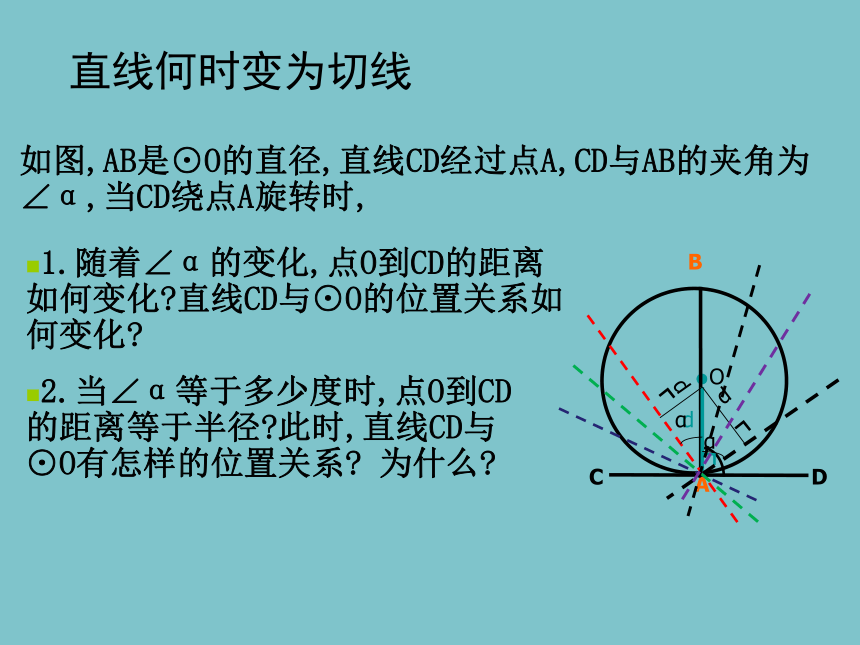
直线何时变为切线
如图,AB是⊙O的直径,直线CD经过点A,CD与AB的夹角为∠α,当CD绕点A旋转时,
1.随着∠α的变化,点O到CD的距离如何变化?直线CD与⊙O的位置关系如何变化?
2.当∠α等于多少度时,点O到CD的距离等于半径?此时,直线CD与⊙O有怎样的位置关系? 为什么?
B
●O
A
C
D
┓
d
α
┏
d
α
d
┓
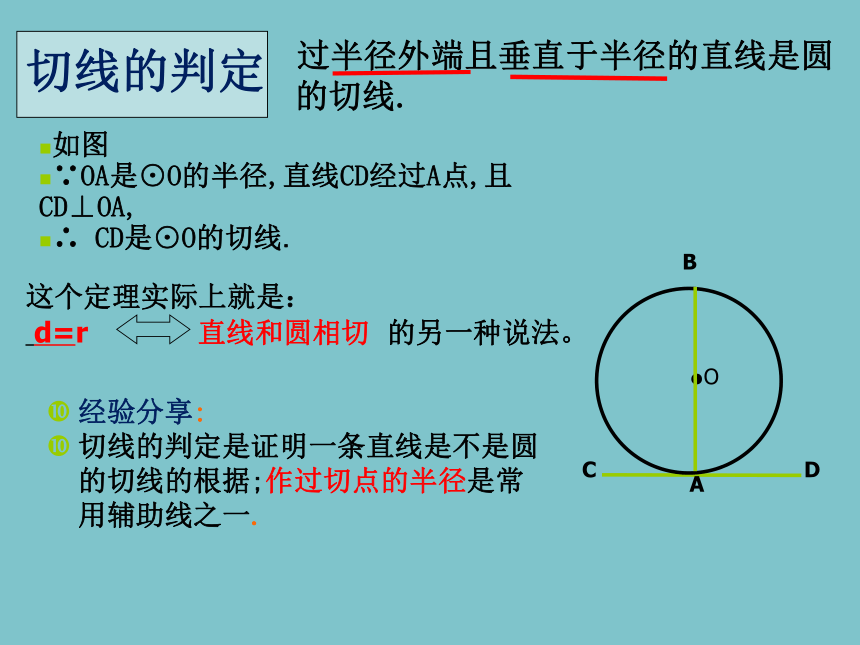
切线的判定
过半径外端且垂直于半径的直线是圆的切线.
经验分享:
切线的判定是证明一条直线是不是圆的切线的根据;作过切点的半径是常用辅助线之一.
C
D
B
●O
A
如图
∵OA是⊙O的半径,直线CD经过A点,且CD⊥OA,
∴ CD是⊙O的切线.
这个定理实际上就是:
d=r 直线和圆相切 的另一种说法。
例1 如图,已知AB为⊙O的直径,点D在AB的延长线上,
BD=OB,点C在圆上,∠CAB=30°.
求证:DC是⊙O的切线.
因为点C在圆上,所以连接OC,
证明OC⊥CD,而要证OC⊥CD,
只需证△OCD为直角三角形.
分析:
证明:如图,连接OC,BC.
∵AB为⊙O的直径,∴∠ACB=90°.
∵∠CAB=30°,∴BC= AB=OB.
又∵BD=OB,∴BC=BD=OB= OD,
∴∠OCD=90°.
∴DC是⊙O的切线.
切线的判定方法有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;(题目未提及直线与圆的明确的交点,通常作过圆心作直线的垂线段)
③切线的判定定理.(题目明确说明直线与圆有某个交点,通常连半径,证垂直)即
经过半径的外端并且垂直这条半径的直线是圆的
切线.
切线证明方法小结
如图所示,PA与⊙O相切于点A,PO交⊙O于点C,点B是优弧CA上一点,若∠ABC=28°,则∠P的度数为( )
A.26°
B.34°
C.32°
D.36°
B
牛刀小试
探索:从一块三角形材料中,能否剪下一个圆,使其与各边都相切?
A
B
C
A
B
C
┓
┗
┗
┓
I●
●
┓
┗
┗
┓
┗
┗
┓
┗
┗
I●
┓
●
作法:
D
(1)作∠ABC、∠ACB的平分线BM和CN,交点为I.
(2)过点I作ID⊥BC,垂足为D.
(3)以I为圆心,ID为半径作⊙I, ⊙I就是所求
M
N
三角形与圆的位置关系
这样的圆可以作出几个呢?为什么?.
∵直线BE和CF只有一个交点I,并且点I到△ABC三边的距离相等(为什么?),
因此和△ABC三边都相切的圆可以作出一个,并且只能作一个.
A
B
C
I●
┓
●
E
F
定义:与三角形三边都相切的圆叫做三角形的内切圆.这个三角形叫做圆的外切三角形.
内切圆的圆心叫做三角形的内心,是三角形三条角平分线的交点.
图形
⊙O的名称
△ABC的名称
圆心O的确定
“心”的性质
“心”的位置
△ABC的内切圆
⊙O的外切三角形
三角形三条角平分线的交点
到三角形的三条边的距离相等
一定在三角形内部
下列关于三角形的内心和外心的说法中,正确的说
法为( )
①三角形的内心是三角形内切圆的圆心;
②三角形的内心是三个角平分线的交点;
③三角形的外心到三边的距离相等;
④三角形的外心是三边中线的交点.
A.①② B.①②③
C.①②④ D.②③④
例1
A
三个顶点的距离
中垂线
【中考】如图为4×4的网格图,A,B,C,D,O均在格点上,点O是( )
A.△ABC的外心
B.△ACD的外心
C.△ACD的内心
D.△ABC的内心
1
A
中考链接
下列说法:①三角形的一定在三角形的内部;②若点I是△ABC的内心,则AI平分∠BAC;③三角形有唯一的内切圆,圆有唯一的外切三角形.其中正确的有( )
A.0个 B.1个
C.2个 D.3个
2
C
【中考】如图,在△ABC中,∠A=64°,点I是内心,则∠BIC的大小为( )
A.114°
B.122°
C.123°
D.132°
3
B
提示:内心是三条角平分线的交点
1.切线的判定:过半径外端且垂直于半径的直线是圆的切线
2.定义:与三角形三边都相切的圆叫做三角形的内切圆.这个三角形叫做圆的外切三角形. 内切圆的圆心叫做三角形的内心,是三角形三条角平分线的交点.
3.锐角三角形、直角三角形、钝角三角形的内切圆的内心都在三角形内部。
切线的判定方法有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;(题目未提及直线与圆的明确的交点,通常作过圆心作直线的垂线段)
③切线的判定定理.(题目明确说明直线与圆有某个交点,通常连半径,证垂直)即
经过半径的外端并且垂直这条半径的直线是圆的
切线.
方法再次回顾
第2课时 切线的判定
学习目标
一、圆的切线的判定定理。
二、三角形内切圆的概念与不同三角形
内切圆的特点。
直线和圆相交
d r;
d r;
直线和圆相切
直线和圆相离
d r;
直线与圆的位置关系?
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
<
=
>
复习旧知:
定理 圆的切线垂直于过切点的直径.
直线何时变为切线
如图,AB是⊙O的直径,直线CD经过点A,CD与AB的夹角为∠α,当CD绕点A旋转时,
1.随着∠α的变化,点O到CD的距离如何变化?直线CD与⊙O的位置关系如何变化?
2.当∠α等于多少度时,点O到CD的距离等于半径?此时,直线CD与⊙O有怎样的位置关系? 为什么?
B
●O
A
C
D
┓
d
α
┏
d
α
d
┓
切线的判定
过半径外端且垂直于半径的直线是圆的切线.
经验分享:
切线的判定是证明一条直线是不是圆的切线的根据;作过切点的半径是常用辅助线之一.
C
D
B
●O
A
如图
∵OA是⊙O的半径,直线CD经过A点,且CD⊥OA,
∴ CD是⊙O的切线.
这个定理实际上就是:
d=r 直线和圆相切 的另一种说法。
例1 如图,已知AB为⊙O的直径,点D在AB的延长线上,
BD=OB,点C在圆上,∠CAB=30°.
求证:DC是⊙O的切线.
因为点C在圆上,所以连接OC,
证明OC⊥CD,而要证OC⊥CD,
只需证△OCD为直角三角形.
分析:
证明:如图,连接OC,BC.
∵AB为⊙O的直径,∴∠ACB=90°.
∵∠CAB=30°,∴BC= AB=OB.
又∵BD=OB,∴BC=BD=OB= OD,
∴∠OCD=90°.
∴DC是⊙O的切线.
切线的判定方法有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;(题目未提及直线与圆的明确的交点,通常作过圆心作直线的垂线段)
③切线的判定定理.(题目明确说明直线与圆有某个交点,通常连半径,证垂直)即
经过半径的外端并且垂直这条半径的直线是圆的
切线.
切线证明方法小结
如图所示,PA与⊙O相切于点A,PO交⊙O于点C,点B是优弧CA上一点,若∠ABC=28°,则∠P的度数为( )
A.26°
B.34°
C.32°
D.36°
B
牛刀小试
探索:从一块三角形材料中,能否剪下一个圆,使其与各边都相切?
A
B
C
A
B
C
┓
┗
┗
┓
I●
●
┓
┗
┗
┓
┗
┗
┓
┗
┗
I●
┓
●
作法:
D
(1)作∠ABC、∠ACB的平分线BM和CN,交点为I.
(2)过点I作ID⊥BC,垂足为D.
(3)以I为圆心,ID为半径作⊙I, ⊙I就是所求
M
N
三角形与圆的位置关系
这样的圆可以作出几个呢?为什么?.
∵直线BE和CF只有一个交点I,并且点I到△ABC三边的距离相等(为什么?),
因此和△ABC三边都相切的圆可以作出一个,并且只能作一个.
A
B
C
I●
┓
●
E
F
定义:与三角形三边都相切的圆叫做三角形的内切圆.这个三角形叫做圆的外切三角形.
内切圆的圆心叫做三角形的内心,是三角形三条角平分线的交点.
图形
⊙O的名称
△ABC的名称
圆心O的确定
“心”的性质
“心”的位置
△ABC的内切圆
⊙O的外切三角形
三角形三条角平分线的交点
到三角形的三条边的距离相等
一定在三角形内部
下列关于三角形的内心和外心的说法中,正确的说
法为( )
①三角形的内心是三角形内切圆的圆心;
②三角形的内心是三个角平分线的交点;
③三角形的外心到三边的距离相等;
④三角形的外心是三边中线的交点.
A.①② B.①②③
C.①②④ D.②③④
例1
A
三个顶点的距离
中垂线
【中考】如图为4×4的网格图,A,B,C,D,O均在格点上,点O是( )
A.△ABC的外心
B.△ACD的外心
C.△ACD的内心
D.△ABC的内心
1
A
中考链接
下列说法:①三角形的一定在三角形的内部;②若点I是△ABC的内心,则AI平分∠BAC;③三角形有唯一的内切圆,圆有唯一的外切三角形.其中正确的有( )
A.0个 B.1个
C.2个 D.3个
2
C
【中考】如图,在△ABC中,∠A=64°,点I是内心,则∠BIC的大小为( )
A.114°
B.122°
C.123°
D.132°
3
B
提示:内心是三条角平分线的交点
1.切线的判定:过半径外端且垂直于半径的直线是圆的切线
2.定义:与三角形三边都相切的圆叫做三角形的内切圆.这个三角形叫做圆的外切三角形. 内切圆的圆心叫做三角形的内心,是三角形三条角平分线的交点.
3.锐角三角形、直角三角形、钝角三角形的内切圆的内心都在三角形内部。
切线的判定方法有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;(题目未提及直线与圆的明确的交点,通常作过圆心作直线的垂线段)
③切线的判定定理.(题目明确说明直线与圆有某个交点,通常连半径,证垂直)即
经过半径的外端并且垂直这条半径的直线是圆的
切线.
方法再次回顾
