北师大版九年级数学下册课件:1.5 三角函数的应用(共27张PPT)
文档属性
| 名称 | 北师大版九年级数学下册课件:1.5 三角函数的应用(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 12:54:32 | ||
图片预览






文档简介
三角函数的应用
第三讲
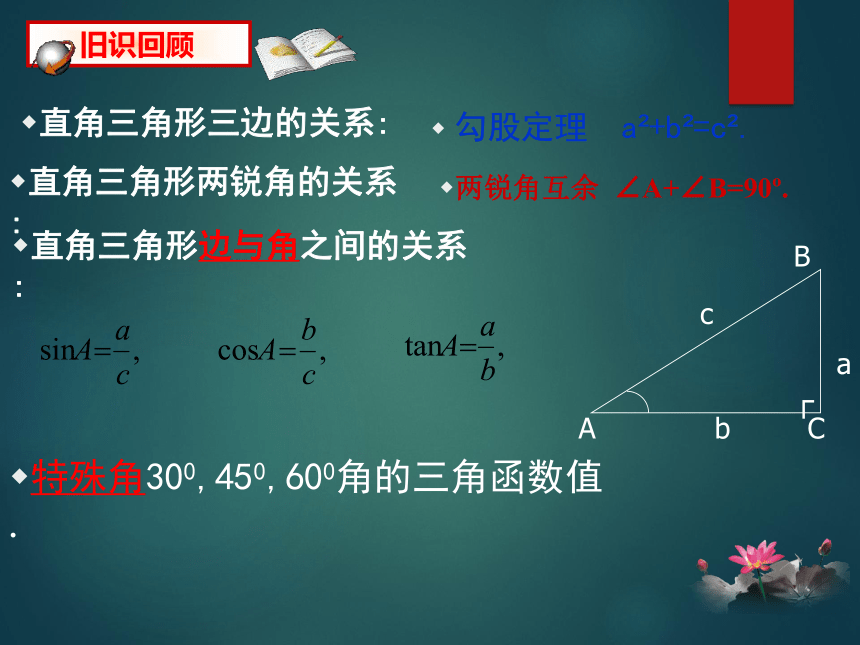
直角三角形两锐角的关系:
直角三角形三边的关系:
旧识回顾
b
A
B
C
a
┌
c
特殊角300,450,600角的三角函数值.
直角三角形边与角之间的关系:
勾股定理 a?+b?=c?.
两锐角互余 ∠A+∠B=90?.
三角函数值 三角函数
角α
sinα
cosα
tanα
30°
45°
60°
1
特殊角300,450,600角的三角函数值.
学而思
1、如图,根据图中已知数据,求△ABC的BC边上的高和△ABC的面积.( 近似取1.7)
解:设AD的长为X cm
∵在Rt△ADC,∠ACD=45?
∴CD=AD=X
∴△ABC的 面积= X4X
∵在Rt△ABC中,∠B=30?,
∴tan30?=
AD
BD
=
A
B
C
450
300
4cm
D
┌
即边上的高是 cm
∴1.7x=x+4
如图,根据图中已知数据,求AD.
A
B
C
550
250
20
D
┌
思而学
老师的提示:
你认为本题的解法与上题有什么区别和联系?
(sin25?= 0.4 ,tan25?= 0.5 sin55?=0.8 tan55?=1.4)
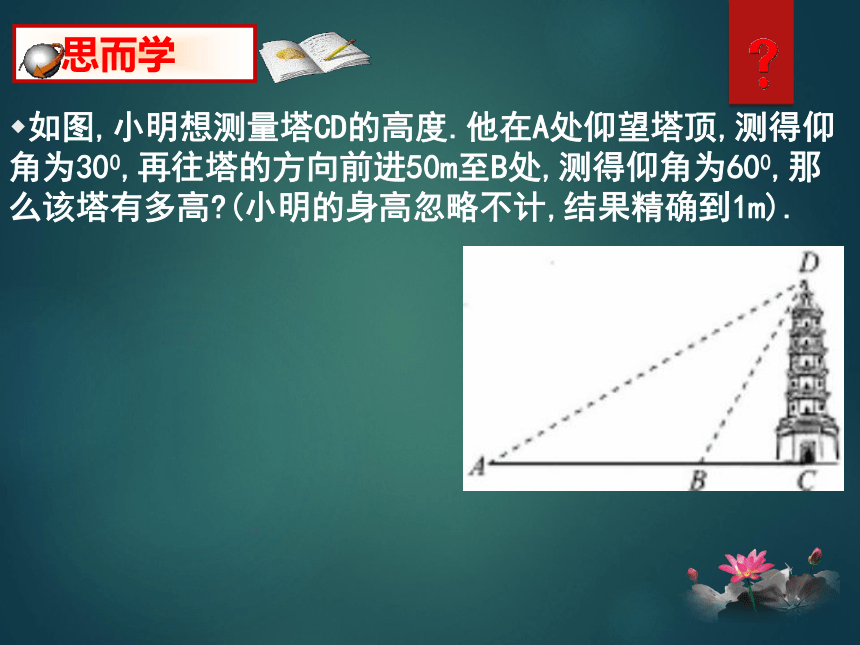
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为300,再往塔的方向前进50m至B处,测得仰角为600,那么该塔有多高?(小明的身高忽略不计,结果精确到1m).
思而学
D
A
B
C
┌
50m
300
600
答:该塔约有43m高.
解法1:如图,根据题意知,∠A=300,∠DBC=600,AB=50m.
设CD=x,则∠ADC=60?,∠BDC=30?,
在Rt△ADC中,tan60?=
在Rt△BDC中,tan30?=
∵AC-BC=AB
在Rt△ADC中,tan60?=
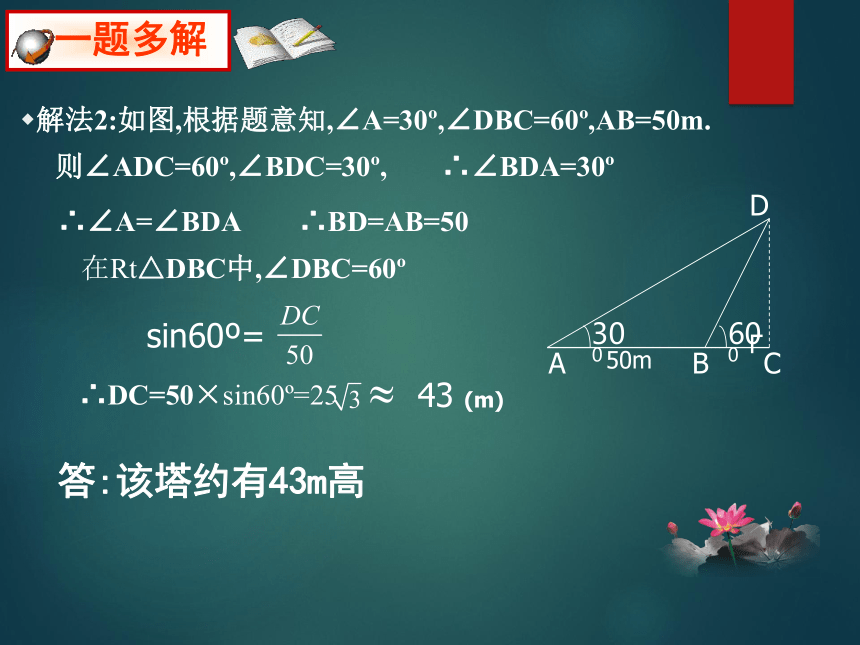
一题多解
解法2:如图,根据题意知,∠A=30?,∠DBC=60?,AB=50m.
则∠ADC=60?,∠BDC=30?,
D
A
B
C
┌
50m
300
600
∴∠BDA=30?
∴∠A=∠BDA
∴BD=AB=50
在Rt△DBC中,∠DBC=60?
sin60?=
∴DC=50×sin60?=25
43
(m)
答:该塔约有43m高
某商场准备改善原有楼梯的安全性能,把倾角由原来的400减至350,已知原楼梯的长度为4m,调整后的楼梯会加长多少?楼梯多占多长一段地面?(结果精确到0.01m).(sin400=0.643,sin350=0.574)
蜗牛
A
B
C
D
┌
解:如图,根据题意可知,∠A=350,∠BDC=400,DB=4m.求(1)AB-BD的长,(2)AD的长.
A
B
C
D
┌
4m
350
400
答:调整后的楼梯会加长约0.48m.
解:如图,根据题意可知,∠A=350,∠BDC=400,DB=4m.求
(2) AD的长.
A
B
C
D
┌
4m
350
400
答:楼梯多占约0.61m一段地面.
如图,一灯柱AB被一钢缆CD固定.CD与地面成400夹角,且DB=5m.现再在CD上方2m处加固另一根钢缆ED,那么,钢缆ED的长度为多少?(结果精确到0.01m).
E
B
C
D
2m
400
5m
解:如图,根据题意可知,∠CDB=400,EC=2m,DB=5m.求DE的长.
∴∠BDE≈51.12°.
E
B
C
D
2m
400
5m
答:钢缆ED的长度约为7.97m.
1 如图,有一斜坡AB长40m,坡顶离地面的高度为20m,求此斜坡的倾斜角.
2.有一建筑物,在地面上A点测得其顶点C的仰角为300,向建筑物前进100m至B处,又测得C的仰角为600,求该建筑物的高度(结果精确到0.1m).
3. 如图,燕尾槽的横断面是一个等腰梯形,其中燕尾角∠B=550,外口宽AD=180mm,燕尾槽的尝试是70mm,求它的里口宽BC(结果精确到1mm).
A
B
C
┌
A
B
C
D
如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗.经测量,得到大门的高度是5m,大门距主楼的距离是30m,在大门处测得主楼顶部的仰角是30°,而当时侧倾器离地面1.4m,求学校主楼的高度
(精确到0.01m)
解:如图,作EM垂直CD于M点,根据题意,可知
EB=1.4m,∠DEM=30°,BC=EM=30 m, CM=BE=1.4m
在Rt△DEM中,DM=EMtan30°≈30×0.577 =17.32(m)
CD=DM+CM=17.32+1.4=18.72(m)
M
大楼AD的高为100米,远处有一塔BC,某人在楼底A处测得塔顶B处的仰角为60°,爬到楼顶D测得塔顶B点仰角为30°,求塔BC的高度.
A
C
B
D
随堂练习
1 如图1-6-13所 示, 某小区楼房附近有一个斜 坡, 小张发现楼房在阳光下的影子落在水平地面与斜坡 上, 在斜坡上的影子长CD=6 m, 坡底到楼房的距离CB=8m, 在点D处观察点A的仰角为54° . 已知坡角为30° , 你能求出楼房AB的高度吗?(结果精确到0.1 m, 参考数据:tan54°≈1.376, sin54°≈0.809, cos54°≈0.588)
解:(1)如图1-6-13, 过点D作DE⊥BC, DF⊥AB, 垂足分别为E, F.
在Rt△ECD中, CD=6 m, ∠ECD=30° ,
∴DE=FB=CD·sin30°=3 m, EC=CD· cos30°=
∴DF=EB=CB+EC=
∵在Rt△ADF中,
∴AF=DF·tan∠ADF= × tan54°≈18.16(m),
∴AB=AF+FB≈18.16+3≈21.2(m).
2 、某市在创建全国文明城市的过程中, 某社区在甲楼的A处与E处之间悬 挂了一个宣传条幅, 在乙楼顶部C点测得条幅顶端 A点的仰角为45° , 条幅底端
E点的俯角为30° , 若 甲、乙两楼之间的水
平距离BD为12米, 求条幅AE 的长度.
(结果保留根号)
解: 过点C作CF⊥AB于点F, 如图1-6-15所示, 由题意知四边形CDBF为矩形, BD=12米, ∴CF=BD=12米.
∵在Rt△ACF中, ∠ACF=45° ,
∴AF=12米.
∵在Rt△CEF中, ∠ECF=30° ,
3 某处山坡上现有一座发射塔被冰雪从C处压折, 塔尖恰好落在坡面上的点B处, 在B处 测得点C的仰角为38°, 塔基 A的俯角为21° , 又测得斜坡上点A到点B的坡面距离AB为15 m. 求折断前发射塔的高.
(结果精确到 0.1 m, 参考数据:
sin21°≈0.358, cos21°≈0.934,
tan21°≈0.384, sin38°≈0.616,
cos38°≈0.788, tan38°≈0.781)
解:过点B作BD⊥AC于点D.
在Rt△ADB中, sin∠ABD= cos∠ABD=
∴AD=AB·sin∠ABD=15×sin21°≈5.37(m), BD=AB·cos∠ABD=15×cos21°≈14.01(m).
在Rt△BDC中, tan∠CBD=
cos∠CBD=
∴CD=BD·tan∠CBD≈14.01×tan38°≈ 10.94(m),
∴AD+CD+BC≈5.37+10.94+17.78=34.09≈ 34.1(m).
因此, 折断前发射塔的高约为34.1 m.
4 如图1-6-17, 线段AB, CD分别表示甲、乙两建筑物的高, BA⊥AD, CD⊥AD, 垂足分别为A, D. 从点D 测得点B的仰角α为60° , 从点C测得点B的仰角β为30°, 甲建筑物的高AB=30米.
(1)求甲、乙两建筑物之间的距离AD;
(2)求乙建筑物的高CD.
解: (1)根据题意, 得在Rt△ABD中, ∠BDA= α=60°, AB=30米,
(2)如图1-6-18, 过点C作CE⊥AB于点E.
根据题意, 得∠BCE=β=30°, CE=AD= CD=AE.
在Rt△CBE中, tan∠BCE=
解得BE=10(米), ∴CD=AE=AB-BE=30-10=20(米).
因此, 乙建筑物的高CD为20米.
5 某数学兴趣小组在活动课上测量学校旗杆的高度. 已知小明的眼睛与地面的距离(AB)是1.7 m, 观测旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(CD)是1.5 m, 观测旗杆顶部M的仰角为30° .
两人相距28 m且位于旗杆两侧
(点B, N, D在同一条直线上).
求旗杆MN 的高度. (结果保留整数)
解:过点A作AE⊥MN于点E, 过 点C作CF⊥MN于点F, 则AB=EN, FN=CD, ∴EF=AB-CD=1.7-1.5=0.2(m).
在Rt△AEM中, ∠MAE=45° , ∴AE=ME. 设AE=ME=x m,
则MF=(x+0.2)m, FC=(28-x)m.
6 观光塔是潍坊市区的标志性建筑, 为测量其高度, 如图1-6-20所示, 一人先在附近一楼房的底端点
A处观测观光塔顶 端C处的仰角是60°, 然后他
爬到该楼房顶端点B处观测观光塔底部D处的
俯角是30° . 已知楼房高AB约是 45 m, 根据以
上观测数据可求出观光塔的高CD约 是 m.
分析 ∵爬到该楼房顶端点B处观测观光塔底部D处的俯角是30°, ∴∠ADB=30°.
在Rt△ABD中,
∵在楼房的底端点A处观测 观光塔顶端C处的仰角是60°, ∴∠CAD=60° ,
∴在Rt△ACD中, CD=AD·tan60°= = 135(m).
谢谢观看
第三讲
直角三角形两锐角的关系:
直角三角形三边的关系:
旧识回顾
b
A
B
C
a
┌
c
特殊角300,450,600角的三角函数值.
直角三角形边与角之间的关系:
勾股定理 a?+b?=c?.
两锐角互余 ∠A+∠B=90?.
三角函数值 三角函数
角α
sinα
cosα
tanα
30°
45°
60°
1
特殊角300,450,600角的三角函数值.
学而思
1、如图,根据图中已知数据,求△ABC的BC边上的高和△ABC的面积.( 近似取1.7)
解:设AD的长为X cm
∵在Rt△ADC,∠ACD=45?
∴CD=AD=X
∴△ABC的 面积= X4X
∵在Rt△ABC中,∠B=30?,
∴tan30?=
AD
BD
=
A
B
C
450
300
4cm
D
┌
即边上的高是 cm
∴1.7x=x+4
如图,根据图中已知数据,求AD.
A
B
C
550
250
20
D
┌
思而学
老师的提示:
你认为本题的解法与上题有什么区别和联系?
(sin25?= 0.4 ,tan25?= 0.5 sin55?=0.8 tan55?=1.4)
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为300,再往塔的方向前进50m至B处,测得仰角为600,那么该塔有多高?(小明的身高忽略不计,结果精确到1m).
思而学
D
A
B
C
┌
50m
300
600
答:该塔约有43m高.
解法1:如图,根据题意知,∠A=300,∠DBC=600,AB=50m.
设CD=x,则∠ADC=60?,∠BDC=30?,
在Rt△ADC中,tan60?=
在Rt△BDC中,tan30?=
∵AC-BC=AB
在Rt△ADC中,tan60?=
一题多解
解法2:如图,根据题意知,∠A=30?,∠DBC=60?,AB=50m.
则∠ADC=60?,∠BDC=30?,
D
A
B
C
┌
50m
300
600
∴∠BDA=30?
∴∠A=∠BDA
∴BD=AB=50
在Rt△DBC中,∠DBC=60?
sin60?=
∴DC=50×sin60?=25
43
(m)
答:该塔约有43m高
某商场准备改善原有楼梯的安全性能,把倾角由原来的400减至350,已知原楼梯的长度为4m,调整后的楼梯会加长多少?楼梯多占多长一段地面?(结果精确到0.01m).(sin400=0.643,sin350=0.574)
蜗牛
A
B
C
D
┌
解:如图,根据题意可知,∠A=350,∠BDC=400,DB=4m.求(1)AB-BD的长,(2)AD的长.
A
B
C
D
┌
4m
350
400
答:调整后的楼梯会加长约0.48m.
解:如图,根据题意可知,∠A=350,∠BDC=400,DB=4m.求
(2) AD的长.
A
B
C
D
┌
4m
350
400
答:楼梯多占约0.61m一段地面.
如图,一灯柱AB被一钢缆CD固定.CD与地面成400夹角,且DB=5m.现再在CD上方2m处加固另一根钢缆ED,那么,钢缆ED的长度为多少?(结果精确到0.01m).
E
B
C
D
2m
400
5m
解:如图,根据题意可知,∠CDB=400,EC=2m,DB=5m.求DE的长.
∴∠BDE≈51.12°.
E
B
C
D
2m
400
5m
答:钢缆ED的长度约为7.97m.
1 如图,有一斜坡AB长40m,坡顶离地面的高度为20m,求此斜坡的倾斜角.
2.有一建筑物,在地面上A点测得其顶点C的仰角为300,向建筑物前进100m至B处,又测得C的仰角为600,求该建筑物的高度(结果精确到0.1m).
3. 如图,燕尾槽的横断面是一个等腰梯形,其中燕尾角∠B=550,外口宽AD=180mm,燕尾槽的尝试是70mm,求它的里口宽BC(结果精确到1mm).
A
B
C
┌
A
B
C
D
如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗.经测量,得到大门的高度是5m,大门距主楼的距离是30m,在大门处测得主楼顶部的仰角是30°,而当时侧倾器离地面1.4m,求学校主楼的高度
(精确到0.01m)
解:如图,作EM垂直CD于M点,根据题意,可知
EB=1.4m,∠DEM=30°,BC=EM=30 m, CM=BE=1.4m
在Rt△DEM中,DM=EMtan30°≈30×0.577 =17.32(m)
CD=DM+CM=17.32+1.4=18.72(m)
M
大楼AD的高为100米,远处有一塔BC,某人在楼底A处测得塔顶B处的仰角为60°,爬到楼顶D测得塔顶B点仰角为30°,求塔BC的高度.
A
C
B
D
随堂练习
1 如图1-6-13所 示, 某小区楼房附近有一个斜 坡, 小张发现楼房在阳光下的影子落在水平地面与斜坡 上, 在斜坡上的影子长CD=6 m, 坡底到楼房的距离CB=8m, 在点D处观察点A的仰角为54° . 已知坡角为30° , 你能求出楼房AB的高度吗?(结果精确到0.1 m, 参考数据:tan54°≈1.376, sin54°≈0.809, cos54°≈0.588)
解:(1)如图1-6-13, 过点D作DE⊥BC, DF⊥AB, 垂足分别为E, F.
在Rt△ECD中, CD=6 m, ∠ECD=30° ,
∴DE=FB=CD·sin30°=3 m, EC=CD· cos30°=
∴DF=EB=CB+EC=
∵在Rt△ADF中,
∴AF=DF·tan∠ADF= × tan54°≈18.16(m),
∴AB=AF+FB≈18.16+3≈21.2(m).
2 、某市在创建全国文明城市的过程中, 某社区在甲楼的A处与E处之间悬 挂了一个宣传条幅, 在乙楼顶部C点测得条幅顶端 A点的仰角为45° , 条幅底端
E点的俯角为30° , 若 甲、乙两楼之间的水
平距离BD为12米, 求条幅AE 的长度.
(结果保留根号)
解: 过点C作CF⊥AB于点F, 如图1-6-15所示, 由题意知四边形CDBF为矩形, BD=12米, ∴CF=BD=12米.
∵在Rt△ACF中, ∠ACF=45° ,
∴AF=12米.
∵在Rt△CEF中, ∠ECF=30° ,
3 某处山坡上现有一座发射塔被冰雪从C处压折, 塔尖恰好落在坡面上的点B处, 在B处 测得点C的仰角为38°, 塔基 A的俯角为21° , 又测得斜坡上点A到点B的坡面距离AB为15 m. 求折断前发射塔的高.
(结果精确到 0.1 m, 参考数据:
sin21°≈0.358, cos21°≈0.934,
tan21°≈0.384, sin38°≈0.616,
cos38°≈0.788, tan38°≈0.781)
解:过点B作BD⊥AC于点D.
在Rt△ADB中, sin∠ABD= cos∠ABD=
∴AD=AB·sin∠ABD=15×sin21°≈5.37(m), BD=AB·cos∠ABD=15×cos21°≈14.01(m).
在Rt△BDC中, tan∠CBD=
cos∠CBD=
∴CD=BD·tan∠CBD≈14.01×tan38°≈ 10.94(m),
∴AD+CD+BC≈5.37+10.94+17.78=34.09≈ 34.1(m).
因此, 折断前发射塔的高约为34.1 m.
4 如图1-6-17, 线段AB, CD分别表示甲、乙两建筑物的高, BA⊥AD, CD⊥AD, 垂足分别为A, D. 从点D 测得点B的仰角α为60° , 从点C测得点B的仰角β为30°, 甲建筑物的高AB=30米.
(1)求甲、乙两建筑物之间的距离AD;
(2)求乙建筑物的高CD.
解: (1)根据题意, 得在Rt△ABD中, ∠BDA= α=60°, AB=30米,
(2)如图1-6-18, 过点C作CE⊥AB于点E.
根据题意, 得∠BCE=β=30°, CE=AD= CD=AE.
在Rt△CBE中, tan∠BCE=
解得BE=10(米), ∴CD=AE=AB-BE=30-10=20(米).
因此, 乙建筑物的高CD为20米.
5 某数学兴趣小组在活动课上测量学校旗杆的高度. 已知小明的眼睛与地面的距离(AB)是1.7 m, 观测旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(CD)是1.5 m, 观测旗杆顶部M的仰角为30° .
两人相距28 m且位于旗杆两侧
(点B, N, D在同一条直线上).
求旗杆MN 的高度. (结果保留整数)
解:过点A作AE⊥MN于点E, 过 点C作CF⊥MN于点F, 则AB=EN, FN=CD, ∴EF=AB-CD=1.7-1.5=0.2(m).
在Rt△AEM中, ∠MAE=45° , ∴AE=ME. 设AE=ME=x m,
则MF=(x+0.2)m, FC=(28-x)m.
6 观光塔是潍坊市区的标志性建筑, 为测量其高度, 如图1-6-20所示, 一人先在附近一楼房的底端点
A处观测观光塔顶 端C处的仰角是60°, 然后他
爬到该楼房顶端点B处观测观光塔底部D处的
俯角是30° . 已知楼房高AB约是 45 m, 根据以
上观测数据可求出观光塔的高CD约 是 m.
分析 ∵爬到该楼房顶端点B处观测观光塔底部D处的俯角是30°, ∴∠ADB=30°.
在Rt△ABD中,
∵在楼房的底端点A处观测 观光塔顶端C处的仰角是60°, ∴∠CAD=60° ,
∴在Rt△ACD中, CD=AD·tan60°= = 135(m).
谢谢观看
