广西壮族自治区北京师范大学平果附属学校2020-2021学年第一学期九年级上册数学第20周周测试题(Word版,含答案)
文档属性
| 名称 | 广西壮族自治区北京师范大学平果附属学校2020-2021学年第一学期九年级上册数学第20周周测试题(Word版,含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 410.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 19:38:32 | ||
图片预览


文档简介
北京师范大学平果附属学校九年级数学第20周周测试题
学校:___________姓名:___________班级:___________分数:___________
一、单选题(共24分)
1.下列函数中,是二次函数的是
A. B. C. D.
2.如果,则k的值为______.
A. B. C.1 D.-1
3.在中,,则的正切值为( )
A. B. C. D.
4.若二次函数y=x2-2x的图象经过点(-1,y1),(3,y2),则y1与y2大小关系为()
A.y1> y2 B.y1=y2 C.y1< y2 D.不能确定
5.如图在△ABC中,D、E分别为AB,AC上的点,若DE∥BC,,则=( )
A. B. C. D.
6.如右图要测量小河两岸相对的两点、的距离,可以在小河边取的垂线上的一点,测得米,,则小河宽为( )
A.米 B.米 C.米 D.米
二、填空题(共24分)
7.若二次函数的顶点在x轴上,则b=_________.
8.如图,以点O为位似中心,将四边形ABCD按1:2放大得到四边形A′B′C′D′,则四边形ABCD与四边形A′B′C′D′的面积比是_____.
9.已知△ABC中,∠C=90°,AB=13,AC=5,则sinA=______.
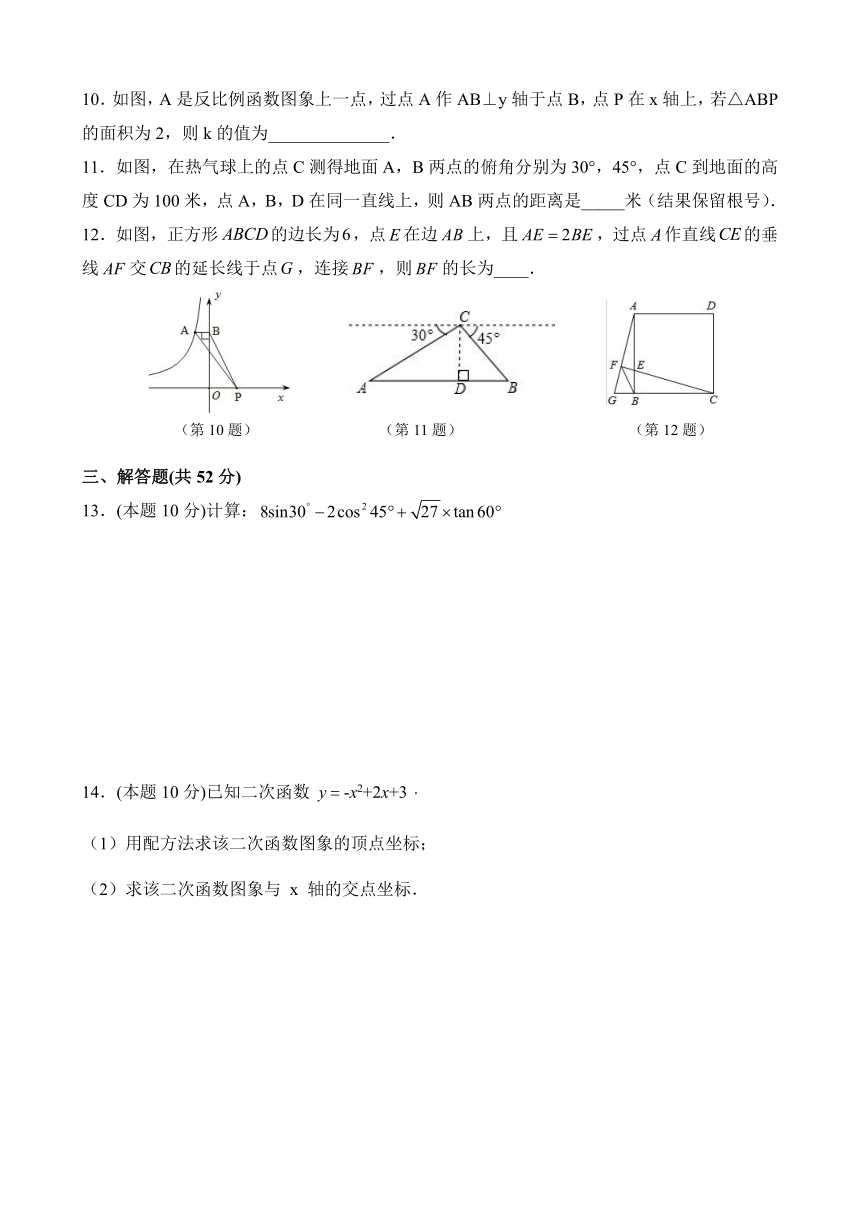
10.如图,A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点P在x轴上,若△ABP的面积为2,则k的值为______________.
11.如图,在热气球上的点C测得地面A,B两点的俯角分别为30°,45°,点C到地面的高度CD为100米,点A,B,D在同一直线上,则AB两点的距离是_____米(结果保留根号).
12.如图,正方形的边长为,点在边上,且,过点作直线的垂线交的延长线于点,连接,则的长为____.
三、解答题(共52分)
13.(本题10分)计算:
14.(本题10分)已知二次函数 y=-x2+2x+3,
(1)用配方法求该二次函数图象的顶点坐标;
(2)求该二次函数图象与 x 轴的交点坐标.
15.(本题10分)如图,甲、乙两人在道路的两边相向而行,当甲、乙两人分别行至点A、C时,测得乙在甲的北偏东60°方向上.乙留在原地休息,甲继续向前走了40米到B处,此时测得乙在其北偏东30°方向上.求道路的宽(参考数据:)
16.(本题10分)如图,平行四边形中,是的延长线上一点,与交于点,。
(1)求证:;
(2)若的面积为4,求平行四边形的面积。
17.(本题12分)如图,抛物线与轴交于,两点,与轴交于点,点与点关于轴对称.
(1)求点,,的坐标;
(2)求直线的解析式;
(3)在直线下方的抛物线上是否存在一点,使的面积最大?若存在,求出点的坐标;若不存在,请说明理由.
(沪科版)北京师范大学平果附属学校第20周周测试题
九年级数学参考答案
一、单选题(共24分)
1.B.2.B,3.B,4.B,5.B,6.A
二、填空题(共24分)
7.2或-2,8.1:4.,9..,10.4,11.100(+1),12.
三、解答题(共52分)
13.解:==4-1+9=12.
14.解:(1)y=﹣x?+2x+3=﹣(x?﹣2x+1﹣1)+3=﹣(x﹣1)?+4,
所以抛物线的顶点坐标为(1,4);
(2)当 y=0 时,﹣x2+2x+3=0,解得 =﹣1,=3,
所以该二次函数图象与 x 轴的交点坐标为(﹣1,0),(3,0).
15.解:过点C作CD⊥AB于点D,则CD的长即为道路的宽.
由题意得∠CAD=30°,∠CBD=60°.
∵∠CBD是△ACB的一个外角,
∴∠ACB=∠CBD-∠CAB=30°.
∴∠CAB=∠ACB,
故AB=PB=40(m).
在Rt△BCD中,∠BDC=90°,∠CBD=60°,CB=40m,
∴CD=CB?sin60°=40×=20≈34.64(米).
∴道路的宽约为34.64米.
16.解:(1)证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AB∥CD,
∴∠ABF=∠CEB,
∴△ABF∽△CEB;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,AB平行且等于CD,
∴△DEF∽△CEB,△DEF∽△ABF,
∵CD=2DE,
∴,,
∵S△DEF=4,
∴S△CEB=36,S△ABF=16,
∴S四边形BCDF=S△BCE?S△DEF=32,
∴S四边形ABCD=S四边形BCDF+S△ABF=32+16=48.
17.解:(1)解方程,得,,
∴点坐标为,点坐标为.
当时,,∴点坐标为.
(2)∵点与点关于轴对称,∴点坐标为.
设直线的解析式为,
则,解得,
∴直线的解析式为.
(3)如图作轴交于,
设,则,
∴,
∴
,
∵,
∴当时,的面积最大,面积的最大值为9,
此时,的坐标为.
学校:___________姓名:___________班级:___________分数:___________
一、单选题(共24分)
1.下列函数中,是二次函数的是
A. B. C. D.
2.如果,则k的值为______.
A. B. C.1 D.-1
3.在中,,则的正切值为( )
A. B. C. D.
4.若二次函数y=x2-2x的图象经过点(-1,y1),(3,y2),则y1与y2大小关系为()
A.y1> y2 B.y1=y2 C.y1< y2 D.不能确定
5.如图在△ABC中,D、E分别为AB,AC上的点,若DE∥BC,,则=( )
A. B. C. D.
6.如右图要测量小河两岸相对的两点、的距离,可以在小河边取的垂线上的一点,测得米,,则小河宽为( )
A.米 B.米 C.米 D.米
二、填空题(共24分)
7.若二次函数的顶点在x轴上,则b=_________.
8.如图,以点O为位似中心,将四边形ABCD按1:2放大得到四边形A′B′C′D′,则四边形ABCD与四边形A′B′C′D′的面积比是_____.
9.已知△ABC中,∠C=90°,AB=13,AC=5,则sinA=______.
10.如图,A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点P在x轴上,若△ABP的面积为2,则k的值为______________.
11.如图,在热气球上的点C测得地面A,B两点的俯角分别为30°,45°,点C到地面的高度CD为100米,点A,B,D在同一直线上,则AB两点的距离是_____米(结果保留根号).
12.如图,正方形的边长为,点在边上,且,过点作直线的垂线交的延长线于点,连接,则的长为____.
三、解答题(共52分)
13.(本题10分)计算:
14.(本题10分)已知二次函数 y=-x2+2x+3,
(1)用配方法求该二次函数图象的顶点坐标;
(2)求该二次函数图象与 x 轴的交点坐标.
15.(本题10分)如图,甲、乙两人在道路的两边相向而行,当甲、乙两人分别行至点A、C时,测得乙在甲的北偏东60°方向上.乙留在原地休息,甲继续向前走了40米到B处,此时测得乙在其北偏东30°方向上.求道路的宽(参考数据:)
16.(本题10分)如图,平行四边形中,是的延长线上一点,与交于点,。
(1)求证:;
(2)若的面积为4,求平行四边形的面积。
17.(本题12分)如图,抛物线与轴交于,两点,与轴交于点,点与点关于轴对称.
(1)求点,,的坐标;
(2)求直线的解析式;
(3)在直线下方的抛物线上是否存在一点,使的面积最大?若存在,求出点的坐标;若不存在,请说明理由.
(沪科版)北京师范大学平果附属学校第20周周测试题
九年级数学参考答案
一、单选题(共24分)
1.B.2.B,3.B,4.B,5.B,6.A
二、填空题(共24分)
7.2或-2,8.1:4.,9..,10.4,11.100(+1),12.
三、解答题(共52分)
13.解:==4-1+9=12.
14.解:(1)y=﹣x?+2x+3=﹣(x?﹣2x+1﹣1)+3=﹣(x﹣1)?+4,
所以抛物线的顶点坐标为(1,4);
(2)当 y=0 时,﹣x2+2x+3=0,解得 =﹣1,=3,
所以该二次函数图象与 x 轴的交点坐标为(﹣1,0),(3,0).
15.解:过点C作CD⊥AB于点D,则CD的长即为道路的宽.
由题意得∠CAD=30°,∠CBD=60°.
∵∠CBD是△ACB的一个外角,
∴∠ACB=∠CBD-∠CAB=30°.
∴∠CAB=∠ACB,
故AB=PB=40(m).
在Rt△BCD中,∠BDC=90°,∠CBD=60°,CB=40m,
∴CD=CB?sin60°=40×=20≈34.64(米).
∴道路的宽约为34.64米.
16.解:(1)证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AB∥CD,
∴∠ABF=∠CEB,
∴△ABF∽△CEB;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,AB平行且等于CD,
∴△DEF∽△CEB,△DEF∽△ABF,
∵CD=2DE,
∴,,
∵S△DEF=4,
∴S△CEB=36,S△ABF=16,
∴S四边形BCDF=S△BCE?S△DEF=32,
∴S四边形ABCD=S四边形BCDF+S△ABF=32+16=48.
17.解:(1)解方程,得,,
∴点坐标为,点坐标为.
当时,,∴点坐标为.
(2)∵点与点关于轴对称,∴点坐标为.
设直线的解析式为,
则,解得,
∴直线的解析式为.
(3)如图作轴交于,
设,则,
∴,
∴
,
∵,
∴当时,的面积最大,面积的最大值为9,
此时,的坐标为.
同课章节目录
