北师大版九年级下册 3.6.1直线与圆的位置关系(2)课件(共22张PPT)
文档属性
| 名称 | 北师大版九年级下册 3.6.1直线与圆的位置关系(2)课件(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 12:28:39 | ||
图片预览





文档简介
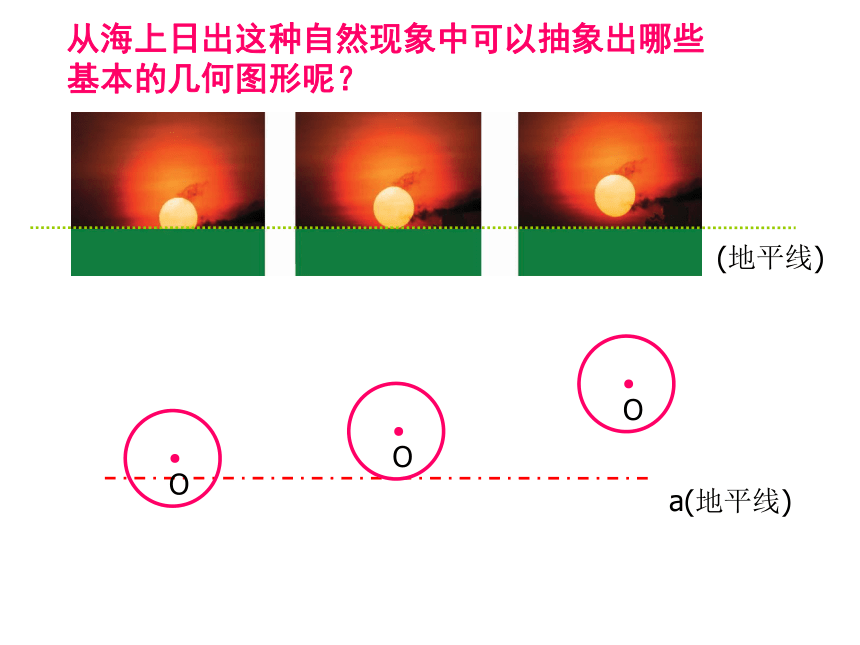
点和圆的位置关系有几种?
点到圆心的距离为d,圆的半径为r,则:
点在圆外 d>r;
点在圆上 d=r;
点在圆内 dA
B
C
位置关系
数形结合:
数量关系
今天老师和同学们一起来探究
(地平线)
a(地平线)
●O
●O
●O
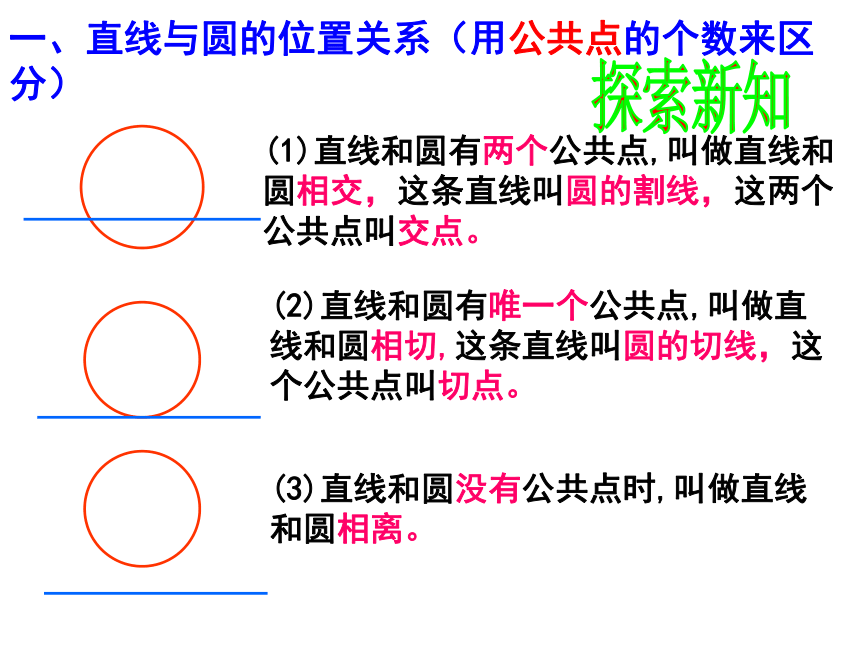
从海上日出这种自然现象中可以抽象出哪些基本的几何图形呢?
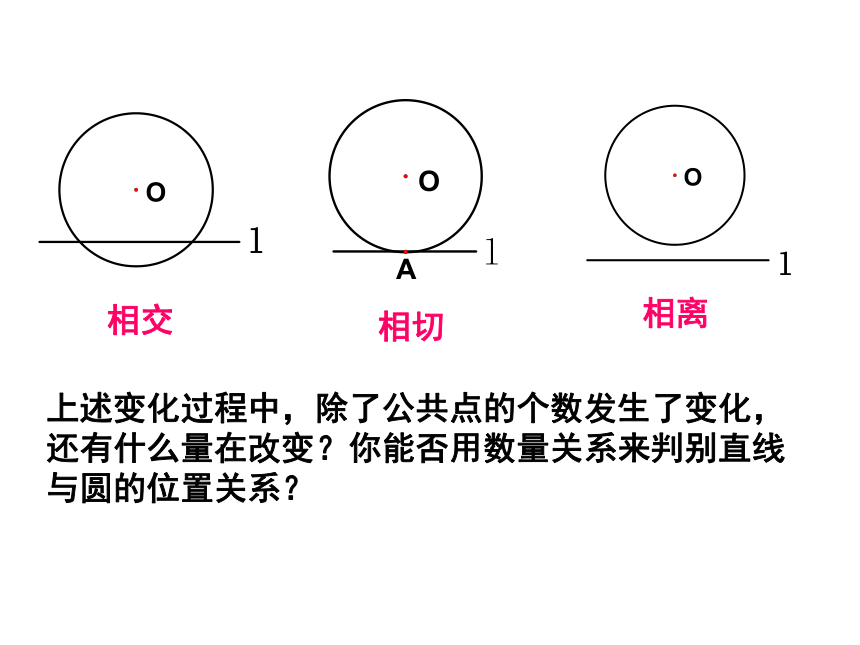
(2)直线和圆有唯一个公共点,叫做直线和圆相切,这条直线叫圆的切线,这个公共点叫切点。
(1)直线和圆有两个公共点,叫做直线和圆相交,这条直线叫圆的割线,这两个公共点叫交点。
(3)直线和圆没有公共点时,叫做直线和圆相离。
一、直线与圆的位置关系(用公共点的个数来区分)
相交
相切
相离
上述变化过程中,除了公共点的个数发生了变化,还有什么量在改变?你能否用数量关系来判别直线与圆的位置关系?
直线和圆相交
d< r
直线和圆相切
d= r
直线和圆相离
d> r
r
d
∟
r
d
∟
r
d
数形结合:
位置关系
数量关系
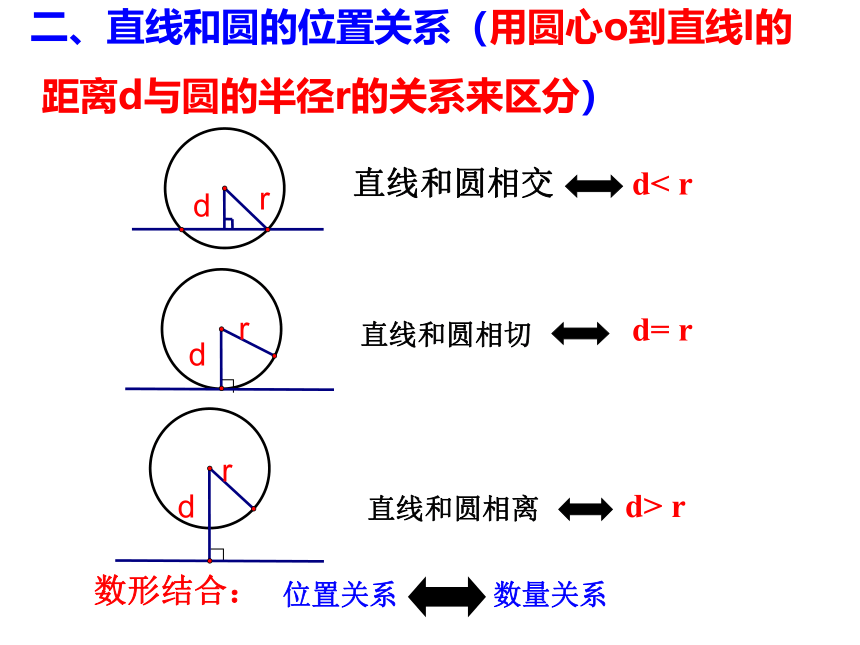
二、直线和圆的位置关系(用圆心o到直线l的
距离d与圆的半径r的关系来区分)
练习一:1、已知圆的直径为13cm,设直线和圆心的距离为d:
1)若d=4.5cm ,则直线与圆________,直线与圆有____个公共点。
2)若d=6.5cm ,则直线与圆________,直线与圆有____个公共点。
3)若d= 8 cm ,则直线与圆________,直线与圆有____个公共点。
2、已知:⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据条件填写d的范围:
1)若AB和⊙O相离, 则______________________。
2)若AB和⊙O相切, 则______________________。
3)若AB和⊙O相交, 则 。
相交
2
相切
1
相离
0
d>5
d=5
d<5
总结:
判定直线与圆的位置关系的方法有____种:
(1)根据定义,由________________
的个数来判断;
(2)根据性质,由_________________
的关系来判断。
在实际应用中,常采用第二种方法判定。
两
直线与圆的公共点
圆心到直线的距离d与半径r
例1
如图,已知Rt△ABC的斜边AB=8cm,直角边AC=4cm
(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切?
(2)以点C为圆心,分别以2cm,4cm为半径作两个圆,这两个圆与AB分别有怎样的位置关系?
D
C
D
B
●O
A
圆的切线的性质
圆的切线垂直于过切
点的半径
例2
AB是⊙O的直径,DF切⊙O于点D,BF⊥DF于F,过点A作AC∥BF交BD的延长线于点C。求证:∠ABC=∠C。
弦切角的定义
顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角。
(弦切角就是切线和弦的夹角)
如图:线段PT所在的直线切圆O于点C,BC、AC为圆O的弦,∠TCB、∠TCA、∠PCA、∠PCB都为弦切角。
弦切角的性质
弦切角等于这条弦和切线所夹的弧所对的圆周角,等于它所夹的弧的圆心角度数的一半。
几何语言:
∵直线PT切圆O于点C,BC、AC为圆O的弦。
∴∠PCA=∠CBA=1/2∠COA
弦切角的性质 证明过程:
已知:直线PT切圆O于点C,BC、AC为圆O的弦。
求证:∠PCA=∠CBA=1/2∠COA
证明:连接OC并延长交圆O于点E
∵弧AB=弧AB
∴∠CBA=∠1
又∵CE是圆O的直径
∴∠1+∠2=90°
又∵直线PT是圆O的切线∴∠PCA+∠2=90°
∴∠PCA=∠1=∠CBA
∵∠CBA=1/2∠AOC
综上所述:∠PCA=∠CBA=1/2∠COA
例3:如图,AD是ΔABC中∠BAC的平分线,经过点A的⊙O与BC切于点D,与AB,AC分别相交于E,F,连结DF。 求证:EF∥BC。
证明:
∵AD是∠BAC的平分线
∴∠1=∠2
∵弧ED=弧ED
∵∠1=∠3
∴∠2=∠3
∵BC是⊙O的切线
∴∠4=∠2
∴∠4=∠3
∴EF∥BC
1、如图,AB切⊙0于点B,AB=4cm,AO=6 cm,则⊙O的半径为________cm。
2、如图,△ABC内接于⊙O,BD切⊙O于点B,AB=AC,若∠CBD=40°,则∠ABC等于_______。
3、如图,AB是⊙0直径,点D在AB延长线上,过点D作⊙0切线,切点为C,若∠A=25°,则∠D=____。
O
B
A
D
C
练习二
70°
40°
4、如图,EB为半圆O的直径,点A在EB的延长线上,AD切半圆O于点D,BC⊥AD于点C,AB=2,半圆O的半径为2,则BC的长为________。
5、如图,PA、PB切⊙O于点A、B,点C是⊙O上一点,且∠ACB=65°,则∠P= 度。
A
B
C
D
O
E
1
50
课后作业:
1、直线L上一点到圆心O的距离等于⊙O的半径,则直线L与⊙O位置关系是( )
A、相离 B、相切
C、相交 D、相切或相交
2、设⊙O的半径为r,点O到直线a的距离为d,若⊙O与直线a至多只有一个公共点,则d与r的关系是( )
A、d≤r B、d<r
C、d≥r D、d=r
D
C
3、已知⊙A的直径为6,点A的坐标为(-3,-4),则⊙A与X轴的位置关系是____________,⊙A与Y轴的位置关系是_____________。
4、圆心O到直线m的距离为d,⊙O半径为R,若d、R是方程x 2-4x+m=0的两根,且直线m与⊙O相切,则m的值为_______。
5、如图, 已知∠AOB=β(β为锐角),点E在OA上,OE=5cm,以E为圆心,2.5cm为半径作⊙E若与直线相切,则β=_________。
相切
相离
4
30°
6、如图,已知△ABC中,∠B=30°,∠A=15°,BC=2,以A为圆心,r为半径作圆A与BC相离,则r的取值范围为__________________。
7、如图,⊙M与轴相交于点A(2,0),B(8,0),与y轴相切于点C,则圆心M的坐标是_________ 。
y
x
M
B
A
O
C
0<r<
(5,4)
8、如图,MP切⊙O于点M,直线PO交⊙O于点A、B,弦AC∥MP,求证:MO∥BC。
9、如图,AB是⊙O的直径,C是圆上一点,CD是⊙O的切线,CD⊥AD于D。
(1)求证:∠CAD=∠CAB;
(2)如果AB=5,cos∠CAB= ,求AD的长。
点到圆心的距离为d,圆的半径为r,则:
点在圆外 d>r;
点在圆上 d=r;
点在圆内 d
B
C
位置关系
数形结合:
数量关系
今天老师和同学们一起来探究
(地平线)
a(地平线)
●O
●O
●O
从海上日出这种自然现象中可以抽象出哪些基本的几何图形呢?
(2)直线和圆有唯一个公共点,叫做直线和圆相切,这条直线叫圆的切线,这个公共点叫切点。
(1)直线和圆有两个公共点,叫做直线和圆相交,这条直线叫圆的割线,这两个公共点叫交点。
(3)直线和圆没有公共点时,叫做直线和圆相离。
一、直线与圆的位置关系(用公共点的个数来区分)
相交
相切
相离
上述变化过程中,除了公共点的个数发生了变化,还有什么量在改变?你能否用数量关系来判别直线与圆的位置关系?
直线和圆相交
d< r
直线和圆相切
d= r
直线和圆相离
d> r
r
d
∟
r
d
∟
r
d
数形结合:
位置关系
数量关系
二、直线和圆的位置关系(用圆心o到直线l的
距离d与圆的半径r的关系来区分)
练习一:1、已知圆的直径为13cm,设直线和圆心的距离为d:
1)若d=4.5cm ,则直线与圆________,直线与圆有____个公共点。
2)若d=6.5cm ,则直线与圆________,直线与圆有____个公共点。
3)若d= 8 cm ,则直线与圆________,直线与圆有____个公共点。
2、已知:⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据条件填写d的范围:
1)若AB和⊙O相离, 则______________________。
2)若AB和⊙O相切, 则______________________。
3)若AB和⊙O相交, 则 。
相交
2
相切
1
相离
0
d>5
d=5
d<5
总结:
判定直线与圆的位置关系的方法有____种:
(1)根据定义,由________________
的个数来判断;
(2)根据性质,由_________________
的关系来判断。
在实际应用中,常采用第二种方法判定。
两
直线与圆的公共点
圆心到直线的距离d与半径r
例1
如图,已知Rt△ABC的斜边AB=8cm,直角边AC=4cm
(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切?
(2)以点C为圆心,分别以2cm,4cm为半径作两个圆,这两个圆与AB分别有怎样的位置关系?
D
C
D
B
●O
A
圆的切线的性质
圆的切线垂直于过切
点的半径
例2
AB是⊙O的直径,DF切⊙O于点D,BF⊥DF于F,过点A作AC∥BF交BD的延长线于点C。求证:∠ABC=∠C。
弦切角的定义
顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角。
(弦切角就是切线和弦的夹角)
如图:线段PT所在的直线切圆O于点C,BC、AC为圆O的弦,∠TCB、∠TCA、∠PCA、∠PCB都为弦切角。
弦切角的性质
弦切角等于这条弦和切线所夹的弧所对的圆周角,等于它所夹的弧的圆心角度数的一半。
几何语言:
∵直线PT切圆O于点C,BC、AC为圆O的弦。
∴∠PCA=∠CBA=1/2∠COA
弦切角的性质 证明过程:
已知:直线PT切圆O于点C,BC、AC为圆O的弦。
求证:∠PCA=∠CBA=1/2∠COA
证明:连接OC并延长交圆O于点E
∵弧AB=弧AB
∴∠CBA=∠1
又∵CE是圆O的直径
∴∠1+∠2=90°
又∵直线PT是圆O的切线∴∠PCA+∠2=90°
∴∠PCA=∠1=∠CBA
∵∠CBA=1/2∠AOC
综上所述:∠PCA=∠CBA=1/2∠COA
例3:如图,AD是ΔABC中∠BAC的平分线,经过点A的⊙O与BC切于点D,与AB,AC分别相交于E,F,连结DF。 求证:EF∥BC。
证明:
∵AD是∠BAC的平分线
∴∠1=∠2
∵弧ED=弧ED
∵∠1=∠3
∴∠2=∠3
∵BC是⊙O的切线
∴∠4=∠2
∴∠4=∠3
∴EF∥BC
1、如图,AB切⊙0于点B,AB=4cm,AO=6 cm,则⊙O的半径为________cm。
2、如图,△ABC内接于⊙O,BD切⊙O于点B,AB=AC,若∠CBD=40°,则∠ABC等于_______。
3、如图,AB是⊙0直径,点D在AB延长线上,过点D作⊙0切线,切点为C,若∠A=25°,则∠D=____。
O
B
A
D
C
练习二
70°
40°
4、如图,EB为半圆O的直径,点A在EB的延长线上,AD切半圆O于点D,BC⊥AD于点C,AB=2,半圆O的半径为2,则BC的长为________。
5、如图,PA、PB切⊙O于点A、B,点C是⊙O上一点,且∠ACB=65°,则∠P= 度。
A
B
C
D
O
E
1
50
课后作业:
1、直线L上一点到圆心O的距离等于⊙O的半径,则直线L与⊙O位置关系是( )
A、相离 B、相切
C、相交 D、相切或相交
2、设⊙O的半径为r,点O到直线a的距离为d,若⊙O与直线a至多只有一个公共点,则d与r的关系是( )
A、d≤r B、d<r
C、d≥r D、d=r
D
C
3、已知⊙A的直径为6,点A的坐标为(-3,-4),则⊙A与X轴的位置关系是____________,⊙A与Y轴的位置关系是_____________。
4、圆心O到直线m的距离为d,⊙O半径为R,若d、R是方程x 2-4x+m=0的两根,且直线m与⊙O相切,则m的值为_______。
5、如图, 已知∠AOB=β(β为锐角),点E在OA上,OE=5cm,以E为圆心,2.5cm为半径作⊙E若与直线相切,则β=_________。
相切
相离
4
30°
6、如图,已知△ABC中,∠B=30°,∠A=15°,BC=2,以A为圆心,r为半径作圆A与BC相离,则r的取值范围为__________________。
7、如图,⊙M与轴相交于点A(2,0),B(8,0),与y轴相切于点C,则圆心M的坐标是_________ 。
y
x
M
B
A
O
C
0<r<
(5,4)
8、如图,MP切⊙O于点M,直线PO交⊙O于点A、B,弦AC∥MP,求证:MO∥BC。
9、如图,AB是⊙O的直径,C是圆上一点,CD是⊙O的切线,CD⊥AD于D。
(1)求证:∠CAD=∠CAB;
(2)如果AB=5,cos∠CAB= ,求AD的长。
