北师大版九年级下册3.5 确定圆的条件 课件(共18张PPT)
文档属性
| 名称 | 北师大版九年级下册3.5 确定圆的条件 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 395.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 00:00:00 | ||
图片预览




文档简介
第三章 圆
第5节 确定圆的条件
学习目标
一、理解不在同一直线上的三个点确定一个圆并掌握它的运用.(重点)
二、了解三角形的外接圆和三角形外心的概念. (难点)
复习旧知
1、过一点可以作几条直线?
2、过几点可以确定一条直线?
无数条
两点确定一直线
3、经过几点可以确定一个圆呢?
感悟新知
一、确定圆的条件
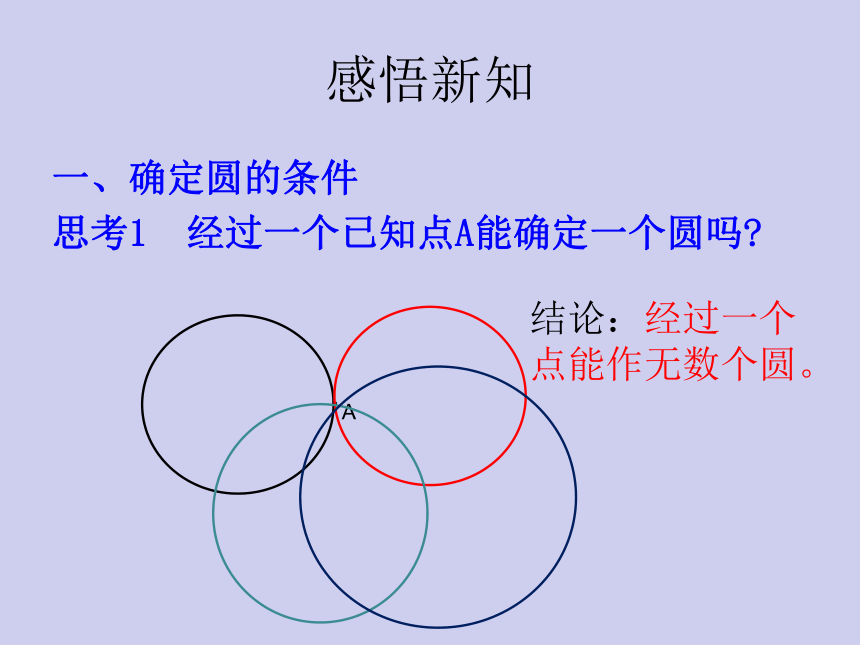
思考1 经过一个已知点A能确定一个圆吗?
·A
结论:经过一个点能作无数个圆。
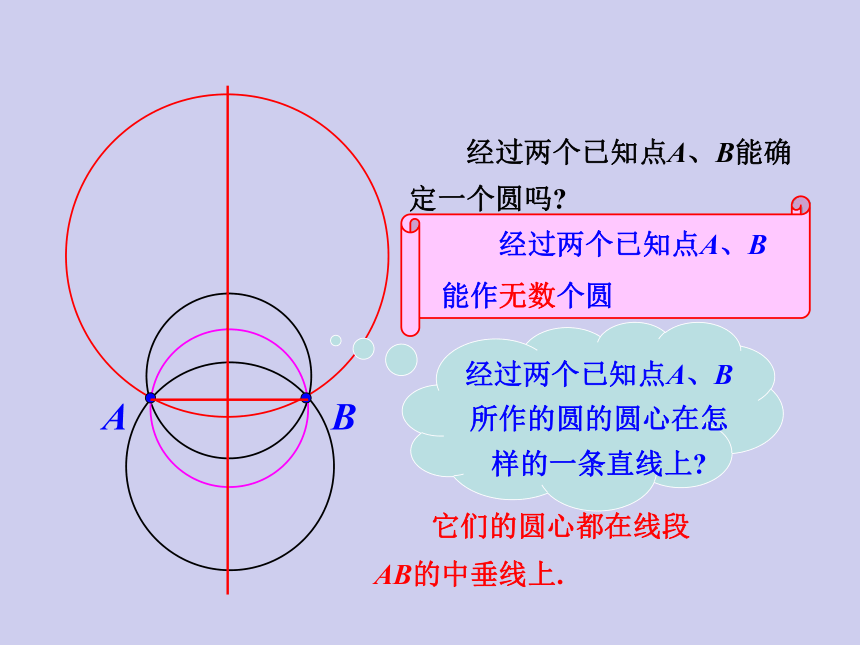
经过两个已知点A、B能确
定一个圆吗?
A
B
它们的圆心都在线段AB的中垂线上.
经过两个已知点A、B
所作的圆的圆心在怎
样的一条直线上?
经过两个已知点A、B能作无数个圆
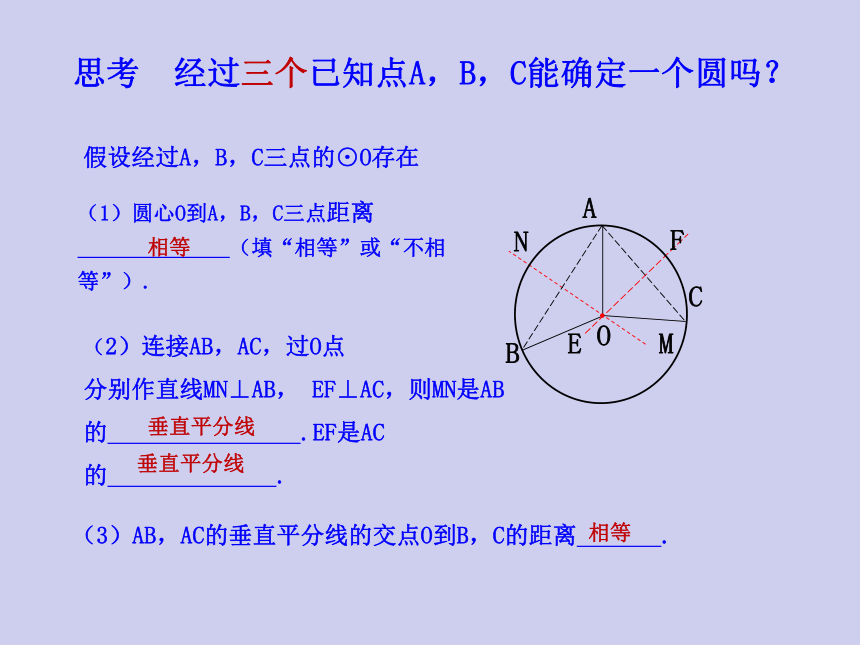
思考 经过三个已知点A,B,C能确定一个圆吗?
假设经过A,B,C三点的⊙O存在
(1)圆心O到A,B,C三点距离
(填“相等”或“不相等”).
(2)连接AB,AC,过O点 分别作直线MN⊥AB, EF⊥AC,则MN是AB的 .EF是AC的 .
(3)AB,AC的垂直平分线的交点O到B,C的距离 .
N
M
F
E
O
A
B
C
相等
垂直平分线
垂直平分线
相等
A
B
C
思考4 过如下三点能不能作一个圆? 为什么?
结论:不在同一条直线上的三个点确定一个圆
已知:不在同一直线上的三点A,B,C,
求作: ⊙O使它经过点A,B,C.
作法:1.连接AB,作线段AB的垂直平分线MN.
2.连接AC,作线段AC的垂直平分线EF,交MN于点O.
3.以O为圆心,OB为半径作圆.⊙O就是所求作的圆.
O
N
M
F
E
A
B
C
例题讲解
结论:不在同一直线的三点确定一个圆,圆心是两点确定线段中垂线的交点,半径为中垂线交点与三点任意一点的距离。
如图①是一个残破的圆轮,李师傅想要再浇铸一个
同样大小的圆轮,你能想办法帮助李师傅吗?
例1
分析:
可先在圆弧上任意取三个点,然后作出两条弦,分别作
这两条弦的垂直平分线即可确定圆轮所在圆的圆心.
解:
如图②:
(1)在圆轮所在的圆弧上任取三
点A,B,C,并连接AB,BC;
(2)分别作AB,BC的垂直平分线
DE,FG,DE,FG相交于点O;
(3)以O为圆心,OA为半径作⊙O,⊙O就是圆轮所
在的圆.
定义:经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心
外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等.
C
A
B
O
二、三角形的外接圆
已知下面的三个三角形,分别作出它们的外接圆. 它们外心的位置有怎样的特点?
1
解:作图略.经观察发现:锐角三角形的外心在三
角形的内部;直角三角形的外心在斜边的中点
处;钝角三角形的外心在三角形的外部.
锐角三角形的外心位于三角形内.
直角三角形的外心位于直角三角形斜边中点.
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
重要结论
下列说法中,真命题的个数是( )
①任何三角形有且只有一个外接圆;② 任何圆有且只有一个内接三角形;③三角形的外心一定在三
角形内;④三角形的外心到三角形三边的距离相等;⑤经过三点确定一个圆.
A.1 B.2 C.3 D.4
1
A
牛刀小试
如图,在平面直角坐标系xOy中,点A的坐标为(0,3),点B的坐标为(2,1),点C的坐标为(2,-3),
则经画图操作可知△ABC的外心坐标应是( )
A.(0,0)
B.(1,0)
C.(-2,-1)
D.(2,0)
2
C
【中考】小谦同学在手工制作中,把一个边
长为18 cm的等边三角形纸片贴到一个圆形纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为( )
A.2 cm B.4 cm
C.6 cm D.8 cm
3
B
下列说法中正确的是( )
A.两个点确定一个圆
B.三个点确定一个圆
C.四个点确定一个圆
D.不共线的三个点确定一个圆
4
D
1.确定圆的条件
不在同一直线上的三点
圆心、半径
3. 锐角三角形 在三角形的内部
直角三角形 --外心的位置--- 在斜边上
钝角三角形 在三角形的外部
课堂小结
2. 三角形有且只有一个外接圆,外接圆的圆心是三边垂 直平分线的交点.
第5节 确定圆的条件
学习目标
一、理解不在同一直线上的三个点确定一个圆并掌握它的运用.(重点)
二、了解三角形的外接圆和三角形外心的概念. (难点)
复习旧知
1、过一点可以作几条直线?
2、过几点可以确定一条直线?
无数条
两点确定一直线
3、经过几点可以确定一个圆呢?
感悟新知
一、确定圆的条件
思考1 经过一个已知点A能确定一个圆吗?
·A
结论:经过一个点能作无数个圆。
经过两个已知点A、B能确
定一个圆吗?
A
B
它们的圆心都在线段AB的中垂线上.
经过两个已知点A、B
所作的圆的圆心在怎
样的一条直线上?
经过两个已知点A、B能作无数个圆
思考 经过三个已知点A,B,C能确定一个圆吗?
假设经过A,B,C三点的⊙O存在
(1)圆心O到A,B,C三点距离
(填“相等”或“不相等”).
(2)连接AB,AC,过O点 分别作直线MN⊥AB, EF⊥AC,则MN是AB的 .EF是AC的 .
(3)AB,AC的垂直平分线的交点O到B,C的距离 .
N
M
F
E
O
A
B
C
相等
垂直平分线
垂直平分线
相等
A
B
C
思考4 过如下三点能不能作一个圆? 为什么?
结论:不在同一条直线上的三个点确定一个圆
已知:不在同一直线上的三点A,B,C,
求作: ⊙O使它经过点A,B,C.
作法:1.连接AB,作线段AB的垂直平分线MN.
2.连接AC,作线段AC的垂直平分线EF,交MN于点O.
3.以O为圆心,OB为半径作圆.⊙O就是所求作的圆.
O
N
M
F
E
A
B
C
例题讲解
结论:不在同一直线的三点确定一个圆,圆心是两点确定线段中垂线的交点,半径为中垂线交点与三点任意一点的距离。
如图①是一个残破的圆轮,李师傅想要再浇铸一个
同样大小的圆轮,你能想办法帮助李师傅吗?
例1
分析:
可先在圆弧上任意取三个点,然后作出两条弦,分别作
这两条弦的垂直平分线即可确定圆轮所在圆的圆心.
解:
如图②:
(1)在圆轮所在的圆弧上任取三
点A,B,C,并连接AB,BC;
(2)分别作AB,BC的垂直平分线
DE,FG,DE,FG相交于点O;
(3)以O为圆心,OA为半径作⊙O,⊙O就是圆轮所
在的圆.
定义:经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心
外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等.
C
A
B
O
二、三角形的外接圆
已知下面的三个三角形,分别作出它们的外接圆. 它们外心的位置有怎样的特点?
1
解:作图略.经观察发现:锐角三角形的外心在三
角形的内部;直角三角形的外心在斜边的中点
处;钝角三角形的外心在三角形的外部.
锐角三角形的外心位于三角形内.
直角三角形的外心位于直角三角形斜边中点.
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
重要结论
下列说法中,真命题的个数是( )
①任何三角形有且只有一个外接圆;② 任何圆有且只有一个内接三角形;③三角形的外心一定在三
角形内;④三角形的外心到三角形三边的距离相等;⑤经过三点确定一个圆.
A.1 B.2 C.3 D.4
1
A
牛刀小试
如图,在平面直角坐标系xOy中,点A的坐标为(0,3),点B的坐标为(2,1),点C的坐标为(2,-3),
则经画图操作可知△ABC的外心坐标应是( )
A.(0,0)
B.(1,0)
C.(-2,-1)
D.(2,0)
2
C
【中考】小谦同学在手工制作中,把一个边
长为18 cm的等边三角形纸片贴到一个圆形纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为( )
A.2 cm B.4 cm
C.6 cm D.8 cm
3
B
下列说法中正确的是( )
A.两个点确定一个圆
B.三个点确定一个圆
C.四个点确定一个圆
D.不共线的三个点确定一个圆
4
D
1.确定圆的条件
不在同一直线上的三点
圆心、半径
3. 锐角三角形 在三角形的内部
直角三角形 --外心的位置--- 在斜边上
钝角三角形 在三角形的外部
课堂小结
2. 三角形有且只有一个外接圆,外接圆的圆心是三边垂 直平分线的交点.
