北师大版九下数学3.9 弧长及扇形的面积教学课件(30张PPT)
文档属性
| 名称 | 北师大版九下数学3.9 弧长及扇形的面积教学课件(30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 774.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 12:29:35 | ||
图片预览











文档简介
第三章 圆
第9节 弧长及扇形的面积
弧、半圆、优弧、劣弧:
圆上任意两点间的部分叫做圆弧,简称弧.
圆的任意一条直径的两个端点分圆成两条
弧,每一条弧都叫做半圆.小于半圆的弧叫做劣弧(如图
中的 ),大于半圆的弧叫做优弧(如图中的 ).劣弧
用“⌒”和弧两端的字母表示;优弧用“⌒ ”和三个字母(弧
两端的字母和弧中间的任一字母)表示.弧分为优弧、半
圆、劣弧.
注意:半圆是弧,但弧不一定是半圆.
1
知识点
弧长公式
如图,某传送带的一个转动轮的半径为10cm.
(1)转动轮转一周,传送带上的物品A
被传送多少 厘米?
(2)转动轮转1°,传送带上的物品A被
传送多少 厘米?
(3)转动轮转n°,传送带上的物品A被传送多少厘米?
知1-导
归 纳
知1-导
在半径为R的圆中, n°的圆心角所对的弧长(arc length)
的计算公式为:
l=________________________.
知1-讲
1.弧长公式:在半径为R的圆中,n°的圆心角所对的
弧长l的计算公式为l= .
要点精析:
(1)应用公式时“n”和“180”不应写单位.
(2)题目若没有写明精确度,可以用含“π”的式子表示弧长.
(3)在弧长公式中,已知l,n,R中任意两个量,都可求出
第三个量.
知1-讲
2.弧、弧长、弧的度数间的关系:
弧相等表示弧长、弧的度数都相等;
度数相等的弧,弧长不一定相等;
弧长相等的弧,弧的度数不一定相等.
3.易错警示:在弧长公式l= 中,n表示1°的n
倍,180表示1°的180倍,n,180不带单位.
知1-讲
制作弯形管道时,需要先按中心线计算 “展直长
度”再下料.试计算如图所示的管道 的展直长度,
即 的长(结果精确到0.1 mm).
例1
解:
R= 40mm,n = 110,所以
的长= 76.8 (mm).
因此,管道的展直长度约为76.8 mm.
知1-讲
〈衡阳〉如图,⊙O的半径为6 cm,直线AB是⊙O的
切线,切点为点B,弦BC∥AO,若∠A=30°,则劣
弧BC的长为________.
例2
导引:
由切线性质可知∠OBA=90°.因为∠A=30°,所以
∠BOA=60°,因为BC∥AO,所以∠CBO=60°.又因
为OB=OC,所以△OBC为等边三角形,所以∠BOC=
60°,代入公式l= =2π(cm).
2π cm
总 结
知1-讲
求弧长需要两个条件:(1)弧所在圆的半径;(2)弧所对
的圆心角.当题中没有直接给出这两个条件时,则需利
用圆的相关知识:弦、弦心距、圆周角、切线等求出圆
的半径或弧所对的圆心角.
知1-练
(2016·包头)120°的圆心角对的弧长是6π,则此弧所在圆的半径是( )
A.3 B.4 C.9 D.18
(2016·成都)AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则 的长为( )
A. π B. π C. π D. π
1
2
知1-练
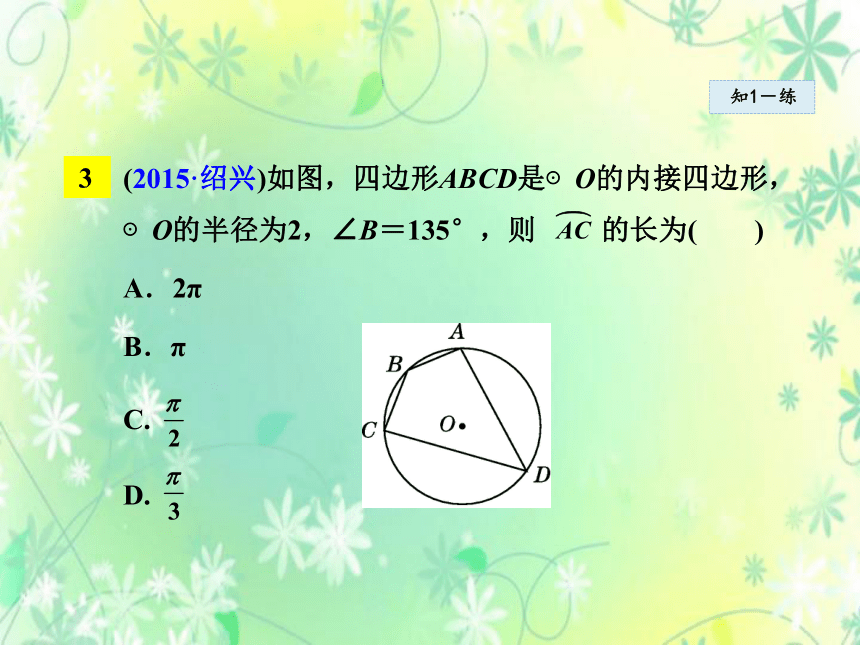
(2015·绍兴)如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则 的长为( )
A.2π
B.π
C.
D.
3
2
知识点
扇形面积公式
知2-导
在一块空旷的草地上有一根柱子,柱子上拴着 一条长
3 m的绳子,绳子的另一端拴着一只狗.
(1)这只狗的最大活动区域有多大?
(2)如果这只狗只能绕柱子转过n°角,
那么它的最大活动区域有多大?
归 纳
知2-导
1.如果扇形的半径为R,圆心角为n° ,那么扇形面积的计
算公式为
S扇形=____________________.
2. 比较扇形面积公式与弧长公式,你能用弧长来表示扇形
的面积吗?
S扇形=____________________l.
知2-讲
1.扇形定义:由组成圆心角的两条半径和圆心角所对
的弧所围成的图形叫做扇形.
2.扇形面积公式:
(1)S扇形= ;
(2)S扇形= lR(l是扇形的弧长).
应用方法:①当已知半径 R 和圆心角的度数求扇形的面
积时,选用公式S扇形= ;
知2-讲
②当已知半径 R 和弧长求扇形的面积时,
选用公式S扇形= lR.
特别注意:
(1)已知S扇形,l,n,R四个量中的任意两个量,可以求出另外
两个量.
(2)在扇形面积公式S扇形= 中,n表示1°的n倍,360表
示1°的360倍,n,360不带单位.
知2-讲
拓展:
(1)弓形定义:由弦及其所对的弧组成的图形叫做弓形.
(2)弓形的面积:①当弓形的弧小于半圆时,它的面积等于扇
形面积与三角形面积的差,即S弓形=S扇形-S三角形;
②当弓形的弧大于半圆时,它的面积等于扇形面积与三角形
面积的和,即S弓形=S扇形+S三角形;
③当弓形的弧是半圆时,它的面积是圆面积的一半,
即S弓形= S圆.
知2-讲
扇形AOB的半径为12 cm, ∠ AOB=120°,求
的长(结果精确到 0.1 cm)和扇形AOB的面积(结果精
确到0.1 cm2).
例3
解:
的长= 25.1 ( cm).
S扇形= 150.7 (cm2 ).
因此, 的长约为25.1 cm,扇形AOB的面积约
为150.7 cm2.
知2-讲
〈广东〉如图,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形DAB的面积为( )
A.6
B.7
C.8
D.9
例4
D
知2-讲
导引:
由正方形的边长为3,可得弧BD的弧长为6,然后利用
扇形的面积公式:S扇形DAB= lR,计算即可.
由条件可知:扇形的弧DCB的长就是正方形的边BC与
CD长的和,为6,半径为3,则S扇形= ×6×3=9.
总 结
知2-讲
扇形的面积计算有两个公式:
1.当已知扇形的圆心角时,用公式S扇形= 较为简便;
2.当知道扇形的弧长时,用公式S扇形= lR较为简便.
知2-讲
如图,在⊙O中,弦BC垂直于半径OA,垂足为点E,D是优弧BC上的一点,∠ADB=30°.
(1)求∠AOC的度数;
(2)若弦BC=6,求图中阴影部分的面积.
例5
知2-讲
导引:
(1)根据垂径定理得到相等的弧,再由同圆或等圆中,
弧、圆心角、圆周角之间的关系求得∠AOC的度数;
(2)先求出⊙O的半径,再求出圆心角∠BOC的度数,
利用面积差求出阴影部分的面积.
知2-讲
解:
(1)∵弦BC垂直于半径OA,∴BE=CE, .
又∵∠ADB=30°,∴∠AOC=∠BOA=60°.
(2)∵BC=6,∴CE= BC=3.
在Rt△OCE中,∠OCE=30°,
设OE=x,则OC=2x,CE= x=3,解得x= .
∴OE= ,OC=2 .∵ ,
∴∠BOC=2∠AOC=120°,∴S阴影=S扇形OBC-S△OBC
= ×π×(2 )2- ×6× =4π-3 .
总 结
知2-讲
本例中求弓形面积可转化为两个规则的基本图形(扇形、
三角形)面积的差来解决.将所求面积转化为其他几个规
则图形面积的和或差,是求阴影面积最常用的方法.
知2-练
(2016·内江)如图,点A,B,C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )
A.π-4
π-1
C. π-2
D. -2
1
知2-练
(2015·咸宁)如图,在△ABC中,CA=CB,
∠ACB=90°,以AB的中点D为圆心,
作圆心角为90°的扇形DEF,点C恰在
上,设∠BDF=α(0°<α<90°).
当α由小到大变化时,图中阴影部分 的面积( )
A.由小变大 B.由大变小
C.不变 D.先由小变大,后由大变小
2
知2-练
(2016·枣庄)如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD= ,则阴影部分的面积为( )
A.2π B.π C. D.
3
知2-练
(2015·泰安)如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD,DC相切,与AB,CB的延长线分别相交于点E,F,则图中阴影部分的面积为( )
A. B. C. D.
4
1
课堂讲解
弧长公式
扇形面积公式
2
课时流程
逐点
导讲练
课堂小结
作业提升
今天你掌握了吗?
1.弧长公式:在半径为R的圆中,n°的圆心角所对
的弧长l的 计算公式为l= .
2.扇形公式:
(1)S扇形= ;
(2)S扇形= lR(l是扇形的弧长).
第9节 弧长及扇形的面积
弧、半圆、优弧、劣弧:
圆上任意两点间的部分叫做圆弧,简称弧.
圆的任意一条直径的两个端点分圆成两条
弧,每一条弧都叫做半圆.小于半圆的弧叫做劣弧(如图
中的 ),大于半圆的弧叫做优弧(如图中的 ).劣弧
用“⌒”和弧两端的字母表示;优弧用“⌒ ”和三个字母(弧
两端的字母和弧中间的任一字母)表示.弧分为优弧、半
圆、劣弧.
注意:半圆是弧,但弧不一定是半圆.
1
知识点
弧长公式
如图,某传送带的一个转动轮的半径为10cm.
(1)转动轮转一周,传送带上的物品A
被传送多少 厘米?
(2)转动轮转1°,传送带上的物品A被
传送多少 厘米?
(3)转动轮转n°,传送带上的物品A被传送多少厘米?
知1-导
归 纳
知1-导
在半径为R的圆中, n°的圆心角所对的弧长(arc length)
的计算公式为:
l=________________________.
知1-讲
1.弧长公式:在半径为R的圆中,n°的圆心角所对的
弧长l的计算公式为l= .
要点精析:
(1)应用公式时“n”和“180”不应写单位.
(2)题目若没有写明精确度,可以用含“π”的式子表示弧长.
(3)在弧长公式中,已知l,n,R中任意两个量,都可求出
第三个量.
知1-讲
2.弧、弧长、弧的度数间的关系:
弧相等表示弧长、弧的度数都相等;
度数相等的弧,弧长不一定相等;
弧长相等的弧,弧的度数不一定相等.
3.易错警示:在弧长公式l= 中,n表示1°的n
倍,180表示1°的180倍,n,180不带单位.
知1-讲
制作弯形管道时,需要先按中心线计算 “展直长
度”再下料.试计算如图所示的管道 的展直长度,
即 的长(结果精确到0.1 mm).
例1
解:
R= 40mm,n = 110,所以
的长= 76.8 (mm).
因此,管道的展直长度约为76.8 mm.
知1-讲
〈衡阳〉如图,⊙O的半径为6 cm,直线AB是⊙O的
切线,切点为点B,弦BC∥AO,若∠A=30°,则劣
弧BC的长为________.
例2
导引:
由切线性质可知∠OBA=90°.因为∠A=30°,所以
∠BOA=60°,因为BC∥AO,所以∠CBO=60°.又因
为OB=OC,所以△OBC为等边三角形,所以∠BOC=
60°,代入公式l= =2π(cm).
2π cm
总 结
知1-讲
求弧长需要两个条件:(1)弧所在圆的半径;(2)弧所对
的圆心角.当题中没有直接给出这两个条件时,则需利
用圆的相关知识:弦、弦心距、圆周角、切线等求出圆
的半径或弧所对的圆心角.
知1-练
(2016·包头)120°的圆心角对的弧长是6π,则此弧所在圆的半径是( )
A.3 B.4 C.9 D.18
(2016·成都)AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则 的长为( )
A. π B. π C. π D. π
1
2
知1-练
(2015·绍兴)如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则 的长为( )
A.2π
B.π
C.
D.
3
2
知识点
扇形面积公式
知2-导
在一块空旷的草地上有一根柱子,柱子上拴着 一条长
3 m的绳子,绳子的另一端拴着一只狗.
(1)这只狗的最大活动区域有多大?
(2)如果这只狗只能绕柱子转过n°角,
那么它的最大活动区域有多大?
归 纳
知2-导
1.如果扇形的半径为R,圆心角为n° ,那么扇形面积的计
算公式为
S扇形=____________________.
2. 比较扇形面积公式与弧长公式,你能用弧长来表示扇形
的面积吗?
S扇形=____________________l.
知2-讲
1.扇形定义:由组成圆心角的两条半径和圆心角所对
的弧所围成的图形叫做扇形.
2.扇形面积公式:
(1)S扇形= ;
(2)S扇形= lR(l是扇形的弧长).
应用方法:①当已知半径 R 和圆心角的度数求扇形的面
积时,选用公式S扇形= ;
知2-讲
②当已知半径 R 和弧长求扇形的面积时,
选用公式S扇形= lR.
特别注意:
(1)已知S扇形,l,n,R四个量中的任意两个量,可以求出另外
两个量.
(2)在扇形面积公式S扇形= 中,n表示1°的n倍,360表
示1°的360倍,n,360不带单位.
知2-讲
拓展:
(1)弓形定义:由弦及其所对的弧组成的图形叫做弓形.
(2)弓形的面积:①当弓形的弧小于半圆时,它的面积等于扇
形面积与三角形面积的差,即S弓形=S扇形-S三角形;
②当弓形的弧大于半圆时,它的面积等于扇形面积与三角形
面积的和,即S弓形=S扇形+S三角形;
③当弓形的弧是半圆时,它的面积是圆面积的一半,
即S弓形= S圆.
知2-讲
扇形AOB的半径为12 cm, ∠ AOB=120°,求
的长(结果精确到 0.1 cm)和扇形AOB的面积(结果精
确到0.1 cm2).
例3
解:
的长= 25.1 ( cm).
S扇形= 150.7 (cm2 ).
因此, 的长约为25.1 cm,扇形AOB的面积约
为150.7 cm2.
知2-讲
〈广东〉如图,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形DAB的面积为( )
A.6
B.7
C.8
D.9
例4
D
知2-讲
导引:
由正方形的边长为3,可得弧BD的弧长为6,然后利用
扇形的面积公式:S扇形DAB= lR,计算即可.
由条件可知:扇形的弧DCB的长就是正方形的边BC与
CD长的和,为6,半径为3,则S扇形= ×6×3=9.
总 结
知2-讲
扇形的面积计算有两个公式:
1.当已知扇形的圆心角时,用公式S扇形= 较为简便;
2.当知道扇形的弧长时,用公式S扇形= lR较为简便.
知2-讲
如图,在⊙O中,弦BC垂直于半径OA,垂足为点E,D是优弧BC上的一点,∠ADB=30°.
(1)求∠AOC的度数;
(2)若弦BC=6,求图中阴影部分的面积.
例5
知2-讲
导引:
(1)根据垂径定理得到相等的弧,再由同圆或等圆中,
弧、圆心角、圆周角之间的关系求得∠AOC的度数;
(2)先求出⊙O的半径,再求出圆心角∠BOC的度数,
利用面积差求出阴影部分的面积.
知2-讲
解:
(1)∵弦BC垂直于半径OA,∴BE=CE, .
又∵∠ADB=30°,∴∠AOC=∠BOA=60°.
(2)∵BC=6,∴CE= BC=3.
在Rt△OCE中,∠OCE=30°,
设OE=x,则OC=2x,CE= x=3,解得x= .
∴OE= ,OC=2 .∵ ,
∴∠BOC=2∠AOC=120°,∴S阴影=S扇形OBC-S△OBC
= ×π×(2 )2- ×6× =4π-3 .
总 结
知2-讲
本例中求弓形面积可转化为两个规则的基本图形(扇形、
三角形)面积的差来解决.将所求面积转化为其他几个规
则图形面积的和或差,是求阴影面积最常用的方法.
知2-练
(2016·内江)如图,点A,B,C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )
A.π-4
π-1
C. π-2
D. -2
1
知2-练
(2015·咸宁)如图,在△ABC中,CA=CB,
∠ACB=90°,以AB的中点D为圆心,
作圆心角为90°的扇形DEF,点C恰在
上,设∠BDF=α(0°<α<90°).
当α由小到大变化时,图中阴影部分 的面积( )
A.由小变大 B.由大变小
C.不变 D.先由小变大,后由大变小
2
知2-练
(2016·枣庄)如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD= ,则阴影部分的面积为( )
A.2π B.π C. D.
3
知2-练
(2015·泰安)如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD,DC相切,与AB,CB的延长线分别相交于点E,F,则图中阴影部分的面积为( )
A. B. C. D.
4
1
课堂讲解
弧长公式
扇形面积公式
2
课时流程
逐点
导讲练
课堂小结
作业提升
今天你掌握了吗?
1.弧长公式:在半径为R的圆中,n°的圆心角所对
的弧长l的 计算公式为l= .
2.扇形公式:
(1)S扇形= ;
(2)S扇形= lR(l是扇形的弧长).
