北师大版七年级数学下册 2.1 两条直线的位置关系(第1课时)( 共21张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 2.1 两条直线的位置关系(第1课时)( 共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 12:35:37 | ||
图片预览







文档简介
两条直线的位置关系(一)
对顶角、余角、补角
观察下列图片,说一说直线与直线的位置关系.
情境引入
生活中处处可见道路、房屋、山川、桥梁.在大自然的杰作和人类的创造物中,蕴含着无数的相交线和平行线.
两条直线的位置关系:
若两条直线只有一个公共顶点,我们称这
两条直线为相交线
在同一平面内,不相交的两条直线叫做平行线。
A
B
C
D
O
1
2
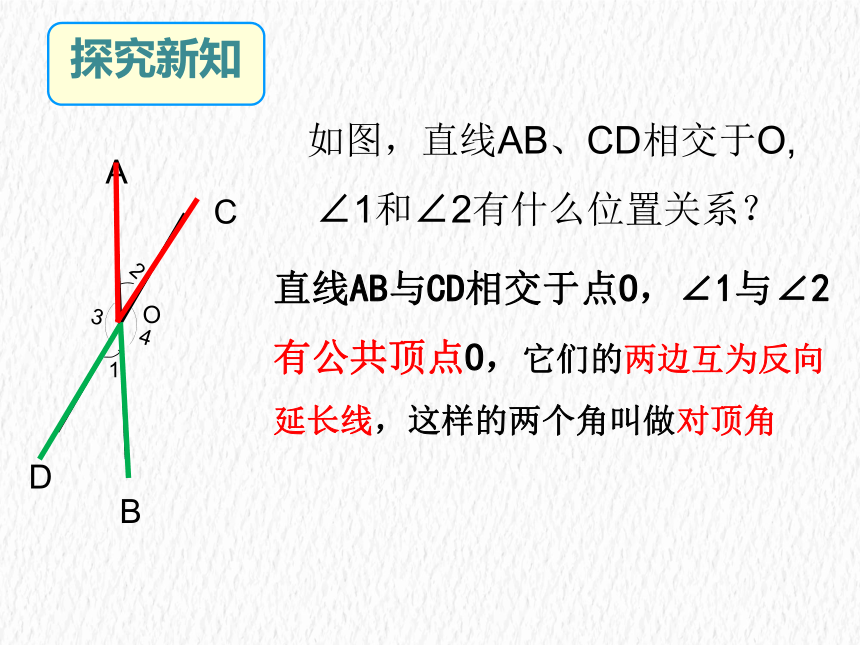
如图,直线AB、CD相交于O,
∠1和∠2有什么位置关系?
直线AB与CD相交于点O,∠1与∠2
有公共顶点O,它们的两边互为反向
延长线,这样的两个角叫做对顶角
3
4
探究新知
A
B
C
D
O
1
2
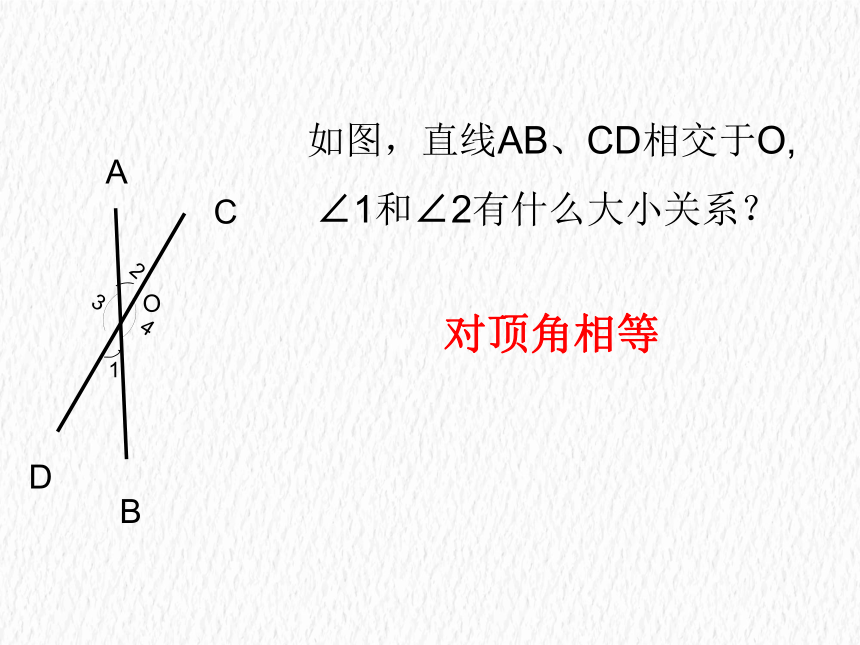
如图,直线AB、CD相交于O,
∠1和∠2有什么大小关系?
对顶角相等
3
4
∠1与∠3有什么数量关系?
A
B
C
D
O
3
1
想一想
如果两个角的和是180°,那么称这
两个角互为补角
∠1+∠3=180°
余角、补角的定义
4
α
β
∠α与 ∠ β有什么数量关系?
∠α+ ∠ β=900
如果两个角的和是90°,那么称这
两个角互为余角。
想一想
图2—2
N
2
D
C
O
1
3
4
A
B
图2-3
打台球时,选择适当的方向,用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2,将图2-2抽象成图2-3,ON与DC交于点O,∠DON=∠CON=900,∠1=∠2。
应用与思考、巩固新知
余角、补角的性质
2
D
C
O
1
3
4
A
B
已知:∠DON=∠CON=900,∠1=∠2
问题1:哪些角互为补角?哪些角互为余角?
问题2:∠3与∠4有什么关系?为什么?
问题3:∠AOC与∠BOD有什么关系?为什么?
∠3=∠4
∠AOC=∠BOD
性质一:同角或等角的余角相等
性质二:同角或等角的补角相等
N
1
2
1
2
1
2
1
2
A
B
C
D
1.下列各图中,∠1和∠2是对顶角的是( )
学以致用 步步为营
__________
2. 小强和小丽一起玩跷跷板(如图所示),
横板AB绕O点上下转动,当小强从A到A'的
位置时,∠AOA'=45°,则∠BOB'度数
为( ),理由是:
3.如图,直线AB、CD相交于O,若∠AOD=134°,
则∠AOC的度数为( )
问题4:如图2.1—11已知:直线AB与CD交于点O,
∠EOD=900,回答下列问题:
1.∠AOE的余角是 ;补角是 。
2.∠AOC的余角是 ;补角是 ;对顶角是 。
C
A
B
D
O
E
2.1─11
5.如图1-2-3,已知∠AOC与∠BOD都是直角,∠BOC=60°.
(1)求∠AOB和∠DOC的度数;
(2)∠AOB与∠DOC有何大小关系;
(3)若不知道∠BOC的具体度数,其他条件不变,这种关系仍然成立吗?请说明理由。
(1) ∠AOB =30°, ∠DOC= 30°
(2) ∠AOB= ∠DOC
(3)成立
∠AOB =90°- ∠BOC
∠DOC =90°- ∠BOC
6..要测量两堵墙所成的角的度数,但人不能进入
围墙,如何测量?
A
B
O
C
D
你有什么收获?
对顶角、余角、补角
观察下列图片,说一说直线与直线的位置关系.
情境引入
生活中处处可见道路、房屋、山川、桥梁.在大自然的杰作和人类的创造物中,蕴含着无数的相交线和平行线.
两条直线的位置关系:
若两条直线只有一个公共顶点,我们称这
两条直线为相交线
在同一平面内,不相交的两条直线叫做平行线。
A
B
C
D
O
1
2
如图,直线AB、CD相交于O,
∠1和∠2有什么位置关系?
直线AB与CD相交于点O,∠1与∠2
有公共顶点O,它们的两边互为反向
延长线,这样的两个角叫做对顶角
3
4
探究新知
A
B
C
D
O
1
2
如图,直线AB、CD相交于O,
∠1和∠2有什么大小关系?
对顶角相等
3
4
∠1与∠3有什么数量关系?
A
B
C
D
O
3
1
想一想
如果两个角的和是180°,那么称这
两个角互为补角
∠1+∠3=180°
余角、补角的定义
4
α
β
∠α与 ∠ β有什么数量关系?
∠α+ ∠ β=900
如果两个角的和是90°,那么称这
两个角互为余角。
想一想
图2—2
N
2
D
C
O
1
3
4
A
B
图2-3
打台球时,选择适当的方向,用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2,将图2-2抽象成图2-3,ON与DC交于点O,∠DON=∠CON=900,∠1=∠2。
应用与思考、巩固新知
余角、补角的性质
2
D
C
O
1
3
4
A
B
已知:∠DON=∠CON=900,∠1=∠2
问题1:哪些角互为补角?哪些角互为余角?
问题2:∠3与∠4有什么关系?为什么?
问题3:∠AOC与∠BOD有什么关系?为什么?
∠3=∠4
∠AOC=∠BOD
性质一:同角或等角的余角相等
性质二:同角或等角的补角相等
N
1
2
1
2
1
2
1
2
A
B
C
D
1.下列各图中,∠1和∠2是对顶角的是( )
学以致用 步步为营
__________
2. 小强和小丽一起玩跷跷板(如图所示),
横板AB绕O点上下转动,当小强从A到A'的
位置时,∠AOA'=45°,则∠BOB'度数
为( ),理由是:
3.如图,直线AB、CD相交于O,若∠AOD=134°,
则∠AOC的度数为( )
问题4:如图2.1—11已知:直线AB与CD交于点O,
∠EOD=900,回答下列问题:
1.∠AOE的余角是 ;补角是 。
2.∠AOC的余角是 ;补角是 ;对顶角是 。
C
A
B
D
O
E
2.1─11
5.如图1-2-3,已知∠AOC与∠BOD都是直角,∠BOC=60°.
(1)求∠AOB和∠DOC的度数;
(2)∠AOB与∠DOC有何大小关系;
(3)若不知道∠BOC的具体度数,其他条件不变,这种关系仍然成立吗?请说明理由。
(1) ∠AOB =30°, ∠DOC= 30°
(2) ∠AOB= ∠DOC
(3)成立
∠AOB =90°- ∠BOC
∠DOC =90°- ∠BOC
6..要测量两堵墙所成的角的度数,但人不能进入
围墙,如何测量?
A
B
O
C
D
你有什么收获?
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
