北师大版七年级数学下册 第1章 第5节 平方差公式 课件(共25张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 第1章 第5节 平方差公式 课件(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 824.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 12:37:48 | ||
图片预览








文档简介
1.5平方差公式
图形法则
相同相反
混合计算
实际应用
2.能熟练判断使用平方差的条件,计算混算结果。
1.体验平方差的法则推导,能画出图形的推导过程。
5.学会独立思考,练习理解,增强自信心。
学习目标
4.学会小组合作,解决遇到的代数与几何问题。
3.能利用平方差解决简单的应用问题。
在一次智力抢答中,主持人提供了两道题:
1、
2、
主持人话音刚落,就立刻有一个学生站起来抢答说:“第一题等于396,第二题等于9999”其速度之快,简直就是脱口而出.同学们,你知道是如何计算的吗?你想不想掌握他的简便、快捷的运算招数呢?
情境引入
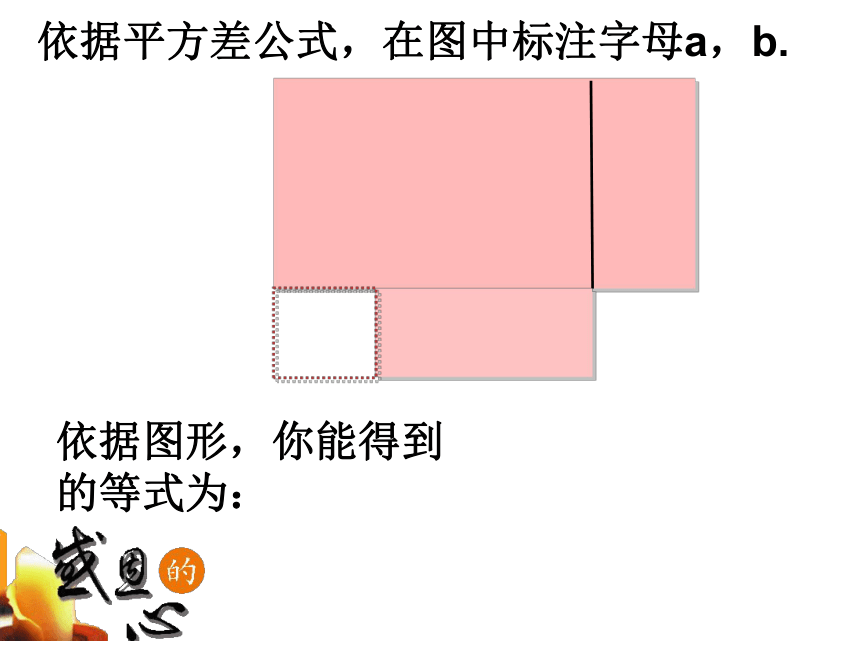
依据平方差公式,在图中标注字母a,b.
依据图形,你能得到的等式为:
计算下列多项式的积,你能发现什么规律?
(x+1)(x-1)=___________;
(m+2)(m-2)=__________;
(2x+1)(2x-1)=_________.
x2-1
m2- 4
4x2-1
(a+b)(a-b)=
a2-b2
新知探究
观察上述算式,等号左边的两个二项式相乘有什么规律?
观察计算结果,你又发现了什么规律?
猜想:
条件探索
代数式
条件
化简结果
(m+4)(m-4)
(-a+2)(-a-2)
(x-5)(x+5)
(mn+3)(mn-3)
(a+5)(b-5)
(a+b)(a-b) =
a2-b2
语言表述:
两个数的和与这两个数的差的积,等于这两个数的平方差
你能用文字语言表示所发现的规律吗?
平方差公式
新知学习
(a+b)(a-b)=a2-b2
相同的数
一对 相反数
用相同数的平方做被减数
公式基本特征:
1、两大项(即同号项、异号项)
2、公式中的字母可以是单项式或是多项式.
新知学习
例 1:运用平方差公式计算:
法则应用
代数式
条件
化简结果
(x+2) (x-2);
(-m+n) (-m-n)
(a2+b) (a2-b)
(-mn+n) (-mn-n)
即时练习
代数式
条件
化简结果
(x+4) (x-4)
(x+y) (x-y)
(-a+3) (-a-3)
(-a2+2) (-a2-2)
1.下列计算对不对?如果不对,怎样改正?
2)
错
1)
分析:最后结果应是两项的平方差
错
3)
分析:应先观察是哪两个数的和与这两个数的差
错
分析:应将 当作一个整体,用括号括起来再平方
自我检测
下列各式能用平方差公式吗?
(x+1)(1+x)
(a+b)(b-a)
(-a+b)(a-b)
(x2-y)(x+y2)
(-a-b)(a-b)
(c2-d2)(d2+c2)
(x+y+1) (x-y-1)
(1)( - )(3x+2y)=9x2-4y2
(2)[0.5+ ]( -0.5)=0.04a2-0.25
3x 2y
自我检测
2.填空
例 2:运用平方差公式计算:
(1) (3x+2) (3x-2);
(2) (-4m+2n) (-4m-2n)
法则应用
即时练习
(1) (2x+5) (2x-5)
(2) (3x2+y) (3x2-y)
(3) (-2a+3) (-2a-3)
(4) (-3a2+2b) (-3a2-2b)
例3 计算:
(1)102×98
(2) (y+2) (y-2) – (y-1) (y+5)
新知应用
1、
2、
解决问题
=(20+2)(20-2)
=(100+1)(100-1)
在一次智力抢答中,主持人提供了两道题:
=202-22
=396
= 1002-12
= 9999
即时练习
(1)20042 - 2003×2005
(2)
(1)(a+3b)(a-3b)
(2)(3+2a)(2a-3)
(3)5.1×4.9
(4)(-2x2-y)(-2x2+y)
自我检测
自我检测
4.计算:
(1)先化简,再求值.其中x=2.
(2)解方程:
计算:
小组讨论
(2+1) (22+1)(24+1) (28+1) +1
(3+1) (32+1)(34+1) (38+1) +1
(5+1) (52+1)(54+1) (58+1) +1
若x2-y2=12 ,x+y=6 ,求x,y的值。
若x+y=-4 ,x-y=8 ,那么x2-y2的值。
已知(2a+2b+1)(2a+2b-1)=63,
那么a+b的值。
平方差公式的简单应用
有一座花园,需要重新设计,现在把一边减少5米,把另一边增加5米,问面积重新设计后是增大了还是减少了?
平方差公式的简单应用
如图所示,小明家有一块L型的菜地,要把L型的菜地按图中所示的样子分成面积相等的两个梯形,种上不同的蔬菜,已知这两个梯形的上底都是a米,下底都是b米,高是(b-a)米.请你给小明家算一算,小明家的菜地的面积是多大?当a=10米,b=30米时,面积是多少?
图形法则
相同相反
混合计算
实际应用
2.能熟练判断使用平方差的条件,计算混算结果。
1.体验平方差的法则推导,能画出图形的推导过程。
5.学会独立思考,练习理解,增强自信心。
学习目标
4.学会小组合作,解决遇到的代数与几何问题。
3.能利用平方差解决简单的应用问题。
在一次智力抢答中,主持人提供了两道题:
1、
2、
主持人话音刚落,就立刻有一个学生站起来抢答说:“第一题等于396,第二题等于9999”其速度之快,简直就是脱口而出.同学们,你知道是如何计算的吗?你想不想掌握他的简便、快捷的运算招数呢?
情境引入
依据平方差公式,在图中标注字母a,b.
依据图形,你能得到的等式为:
计算下列多项式的积,你能发现什么规律?
(x+1)(x-1)=___________;
(m+2)(m-2)=__________;
(2x+1)(2x-1)=_________.
x2-1
m2- 4
4x2-1
(a+b)(a-b)=
a2-b2
新知探究
观察上述算式,等号左边的两个二项式相乘有什么规律?
观察计算结果,你又发现了什么规律?
猜想:
条件探索
代数式
条件
化简结果
(m+4)(m-4)
(-a+2)(-a-2)
(x-5)(x+5)
(mn+3)(mn-3)
(a+5)(b-5)
(a+b)(a-b) =
a2-b2
语言表述:
两个数的和与这两个数的差的积,等于这两个数的平方差
你能用文字语言表示所发现的规律吗?
平方差公式
新知学习
(a+b)(a-b)=a2-b2
相同的数
一对 相反数
用相同数的平方做被减数
公式基本特征:
1、两大项(即同号项、异号项)
2、公式中的字母可以是单项式或是多项式.
新知学习
例 1:运用平方差公式计算:
法则应用
代数式
条件
化简结果
(x+2) (x-2);
(-m+n) (-m-n)
(a2+b) (a2-b)
(-mn+n) (-mn-n)
即时练习
代数式
条件
化简结果
(x+4) (x-4)
(x+y) (x-y)
(-a+3) (-a-3)
(-a2+2) (-a2-2)
1.下列计算对不对?如果不对,怎样改正?
2)
错
1)
分析:最后结果应是两项的平方差
错
3)
分析:应先观察是哪两个数的和与这两个数的差
错
分析:应将 当作一个整体,用括号括起来再平方
自我检测
下列各式能用平方差公式吗?
(x+1)(1+x)
(a+b)(b-a)
(-a+b)(a-b)
(x2-y)(x+y2)
(-a-b)(a-b)
(c2-d2)(d2+c2)
(x+y+1) (x-y-1)
(1)( - )(3x+2y)=9x2-4y2
(2)[0.5+ ]( -0.5)=0.04a2-0.25
3x 2y
自我检测
2.填空
例 2:运用平方差公式计算:
(1) (3x+2) (3x-2);
(2) (-4m+2n) (-4m-2n)
法则应用
即时练习
(1) (2x+5) (2x-5)
(2) (3x2+y) (3x2-y)
(3) (-2a+3) (-2a-3)
(4) (-3a2+2b) (-3a2-2b)
例3 计算:
(1)102×98
(2) (y+2) (y-2) – (y-1) (y+5)
新知应用
1、
2、
解决问题
=(20+2)(20-2)
=(100+1)(100-1)
在一次智力抢答中,主持人提供了两道题:
=202-22
=396
= 1002-12
= 9999
即时练习
(1)20042 - 2003×2005
(2)
(1)(a+3b)(a-3b)
(2)(3+2a)(2a-3)
(3)5.1×4.9
(4)(-2x2-y)(-2x2+y)
自我检测
自我检测
4.计算:
(1)先化简,再求值.其中x=2.
(2)解方程:
计算:
小组讨论
(2+1) (22+1)(24+1) (28+1) +1
(3+1) (32+1)(34+1) (38+1) +1
(5+1) (52+1)(54+1) (58+1) +1
若x2-y2=12 ,x+y=6 ,求x,y的值。
若x+y=-4 ,x-y=8 ,那么x2-y2的值。
已知(2a+2b+1)(2a+2b-1)=63,
那么a+b的值。
平方差公式的简单应用
有一座花园,需要重新设计,现在把一边减少5米,把另一边增加5米,问面积重新设计后是增大了还是减少了?
平方差公式的简单应用
如图所示,小明家有一块L型的菜地,要把L型的菜地按图中所示的样子分成面积相等的两个梯形,种上不同的蔬菜,已知这两个梯形的上底都是a米,下底都是b米,高是(b-a)米.请你给小明家算一算,小明家的菜地的面积是多大?当a=10米,b=30米时,面积是多少?
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
