北师大版七年级数学下册1.5 (2)平方差公式的应用 课件(共16张PPT)
文档属性
| 名称 | 北师大版七年级数学下册1.5 (2)平方差公式的应用 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 232.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 12:39:10 | ||
图片预览





文档简介
1.5 (2)平方差公式的应用
自主学习 交流展示
平方差公式:
(a + b) (a- b) = a 2 - b 2
两数和与这两数差的积,等于它们的平方差.
相同项
相反项
( ) ( )
合作探究 释疑点拨
如图,边长为a的大正方形中有一个边长为b的小正方形.
(1)请表示图中阴影部分的面积。
(2)你能将阴影部分通过裁剪一刀,拼凑成一个规则图形吗?
(3)它的面积又可以怎样表示?
a-b
a
b
a-b
a-b
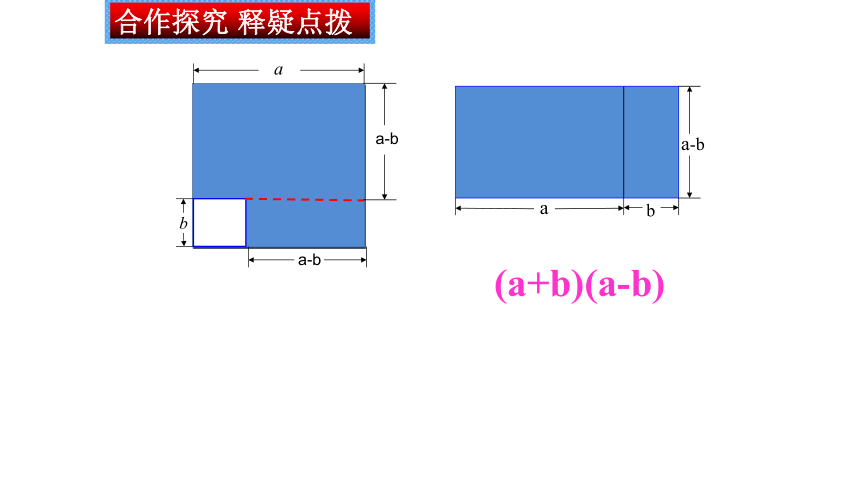
合作探究 释疑点拨
(a+b)(a-b)
b
a-b
a
a-b
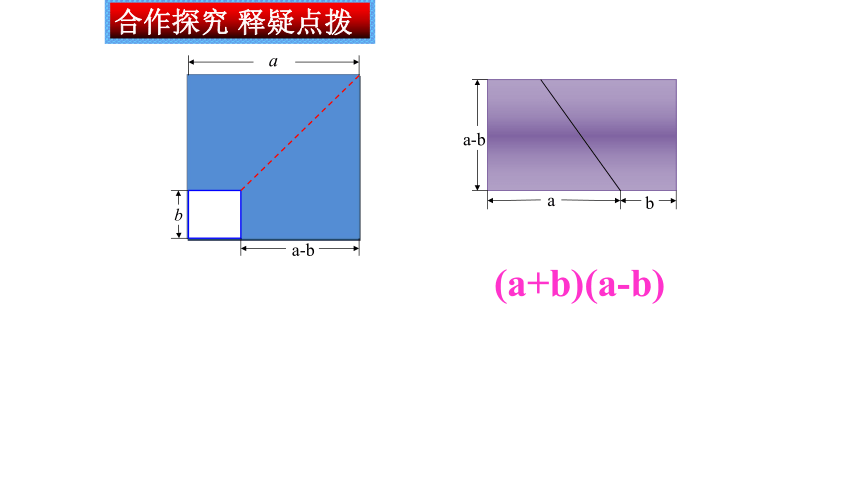
合作探究 释疑点拨
(a+b)(a-b)
b
a
a-b
a-b
合作探究 释疑点拨
(a+b)(a-b)
a-b
b
b
a
a
a-b
合作探究 释疑点拨
(1)计算下列各组算式,并观察它们的共同特点:
合作探究 释疑点拨
7 × 9 =
8 × 8 =
11 × 13 =
12 × 12 =
79 × 81 =
80 × 80 =
63
64
143
144
6399
6400
想一想
(2)由上面的过程中,你发现了什么规律?
(3)如果设这个自然数为n,那么与它相邻的两个数怎样表示?这一规律用字母又怎样表示?你能说明它的正确性吗?
用平方差公式进行简便计算:
合作探究 释疑点拨
例1
103×97
计算:
例2
训练检测 巩固提高
1.练一练
A -1 B 1 C 0 D 2
训练检测 巩固提高
4.计算
训练检测 巩固提高
这节课你有什么收获?
要点梳理,交流收获
要点梳理 交流收获
1.平方差公式的几何解释:图中阴影部分面积相等
2.平方差公式的运用
(a+b)(a-b)=a2-b2
a
b
a-b
——可以简化运算
3.整式的混合运算注意事项:
(1)运算顺序 (2)运算律
(3)加括号 (4)结果化为最简
课后作业:
课本P22 习题1.10
自主学习 交流展示
平方差公式:
(a + b) (a- b) = a 2 - b 2
两数和与这两数差的积,等于它们的平方差.
相同项
相反项
( ) ( )
合作探究 释疑点拨
如图,边长为a的大正方形中有一个边长为b的小正方形.
(1)请表示图中阴影部分的面积。
(2)你能将阴影部分通过裁剪一刀,拼凑成一个规则图形吗?
(3)它的面积又可以怎样表示?
a-b
a
b
a-b
a-b
合作探究 释疑点拨
(a+b)(a-b)
b
a-b
a
a-b
合作探究 释疑点拨
(a+b)(a-b)
b
a
a-b
a-b
合作探究 释疑点拨
(a+b)(a-b)
a-b
b
b
a
a
a-b
合作探究 释疑点拨
(1)计算下列各组算式,并观察它们的共同特点:
合作探究 释疑点拨
7 × 9 =
8 × 8 =
11 × 13 =
12 × 12 =
79 × 81 =
80 × 80 =
63
64
143
144
6399
6400
想一想
(2)由上面的过程中,你发现了什么规律?
(3)如果设这个自然数为n,那么与它相邻的两个数怎样表示?这一规律用字母又怎样表示?你能说明它的正确性吗?
用平方差公式进行简便计算:
合作探究 释疑点拨
例1
103×97
计算:
例2
训练检测 巩固提高
1.练一练
A -1 B 1 C 0 D 2
训练检测 巩固提高
4.计算
训练检测 巩固提高
这节课你有什么收获?
要点梳理,交流收获
要点梳理 交流收获
1.平方差公式的几何解释:图中阴影部分面积相等
2.平方差公式的运用
(a+b)(a-b)=a2-b2
a
b
a-b
——可以简化运算
3.整式的混合运算注意事项:
(1)运算顺序 (2)运算律
(3)加括号 (4)结果化为最简
课后作业:
课本P22 习题1.10
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
