北师大版七年级数学下册第二章2.1.1两直线的位置关系 (共18张PPT)
文档属性
| 名称 | 北师大版七年级数学下册第二章2.1.1两直线的位置关系 (共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 00:00:00 | ||
图片预览





文档简介
北师大版七年级数学下册第二章相交线与平行线
2.1.1两直线的位置关系
一、学习目标
1.在具体情境中了解相交线、平行线、补角、余角、对顶角的定义
2.知道同角或等角的余角相等、同角或等角的补角相等、对顶角相等,
并能解决一些实际问题。
重、难点:补角、余角、对顶角,等角的余角相等、等角的补角相等、
对顶角相等
自主探究:阅读课本p37-40
探究(一)探索在同一平面内,两条直线的位置关系哪两种?
观察下列图片,回答:
结论:
1.一般地,在同一平面内,两条直线的位置关系有两种: 和 .
2.定义分别为:
相交 平行
若两条直线只有一个公共点,称这两条直线相交;
在同一平面内,不相交的两条直线叫做平行线
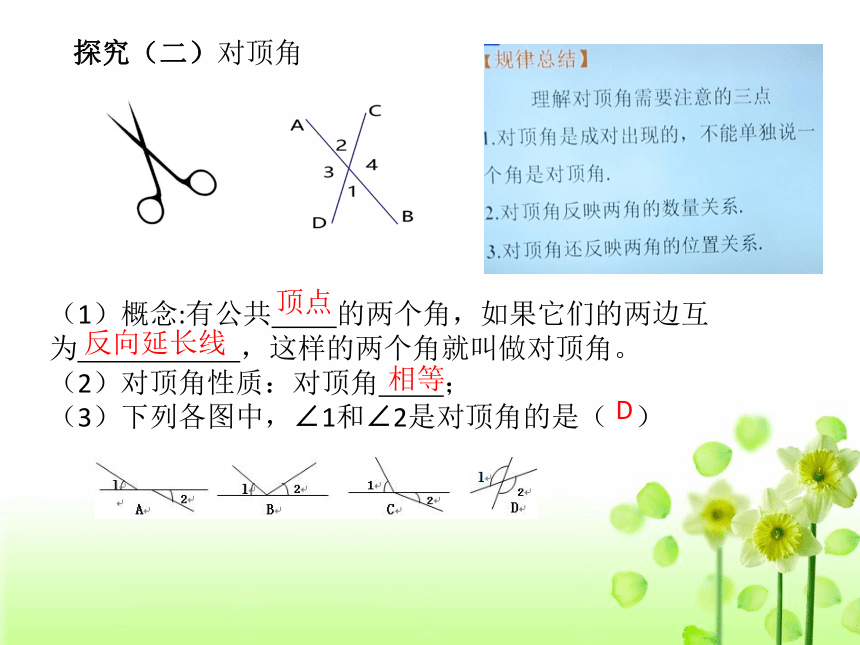
探究(二)对顶角
(1)概念:有公共 的两个角,如果它们的两边互为 ,这样的两个角就叫做对顶角。
(2)对顶角性质:对顶角 ;
(3)下列各图中,∠1和∠2是对顶角的是( )
顶点
反向延长线
相等
D
探究(三) 3、余角与补角
(1)概念
如果两个角的和是 ,那么称这两个角互为余角;
如果两个角的和是 ,那么称这两个角互为补角。
符号语言:
若∠1+∠2= 90o , 那么∠1与∠2互余。
若∠3+∠4=180o , 那么∠3与∠4互补。
(2)填表:
(3)性质
同角或等角的余角 ;同角或等角的补角 为什么?
90°
180°
相等
相等
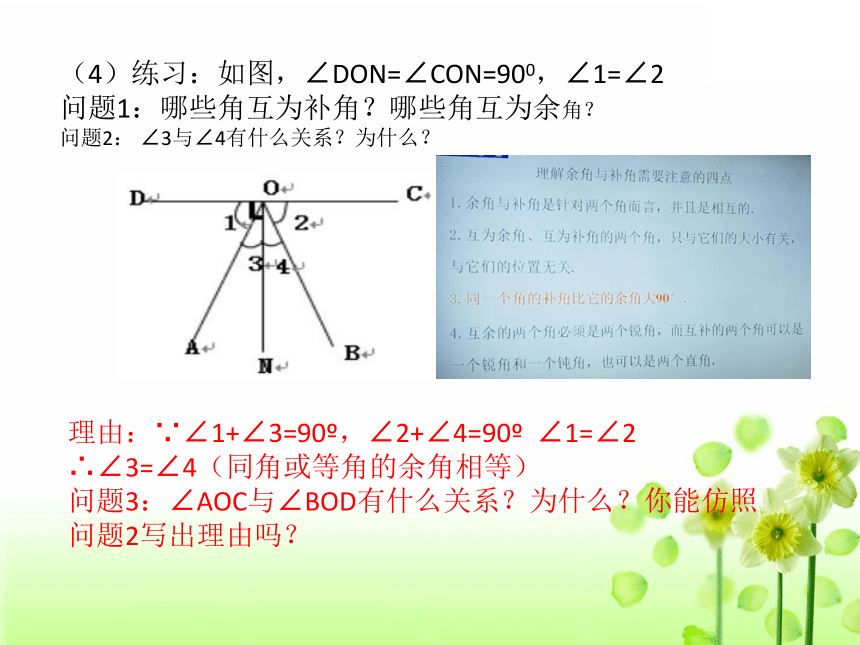
(4)练习:如图,∠DON=∠CON=900,∠1=∠2
问题1:哪些角互为补角?哪些角互为余角?
问题2: ∠3与∠4有什么关系?为什么?
理由:∵∠1+∠3=90?,∠2+∠4=90? ∠1=∠2
∴∠3=∠4(同角或等角的余角相等)
问题3:∠AOC与∠BOD有什么关系?为什么?你能仿照问题2写出理由吗?
三.温故知新
直线的基本性质: .
线段的性质: .
两点之间的距离: .
两点确定一条直线
两点之间线段最短
两点之间线段的长度叫做两点之间的距离
四.随堂练习
如图1,∠C=900 则∠A是∠B的 ;
如图2,∠ACB=900 ∠CDA=900 则∠A的余角有哪几个?为什么?
图1
图2
2.∠B,∠ACD
余角
3、如图,直线AB、CD相交于点O,∠AOE=900 ,则
(1)∠1与∠2互为 角; (2)∠1与∠3互为 角;
(3)∠3与∠4互为 角; (4)∠1与∠4互为 角;
(1)补角;(2)对顶角;(3)余角;(4)余角
五.小结:
你还有哪些收获:
哪些疑问:
六.当堂检测:
1、判断:
(1)一个角的余角一定是锐角 ( )
(2)一个角的补角一定是钝角 ( )
(3)若∠1+∠2+∠3=90°,那么∠1、∠2、∠3互为余角 ( )
2、填空:
(1)一个角和它的余角相等,这个角为___________度
(2)一个角和它的补角相等,这个角为__________度
(3)已知∠A=400 ,则∠A的余角是 ,补角是 .
错
对
错
140°
45°
90°
50°
3、下列说法正确的是( )
A.相等的角是对顶角
B.对顶角相等
C.两条直线相交所成的角是对顶角
D.有公共顶点且又相等的角是对顶角
4.如图,直线a,b相交,∠1=35° ,求∠2,∠3,∠4的度数
B
解:因为∠1=35°,
所以∠3= ∠1=35°(对顶角相等)
因为∠1+ ∠2=180°(平角等于180度)
所以∠2=180°-35°=145°
所以∠4= ∠2=145°(对顶角相等)
课后作业:
1.如图,直线a,b相交,∠1=38°,求∠2, ∠3, ,4的度数。
解:因为∠1=38°,
所以∠3= ∠1=38°(对顶角相等)
因为∠1+ ∠2=180°(平角等于180度)
所以∠2=180°-38°=142°
所以∠4= ∠2=142°(对顶角相等)
2.互为补角的两个角可以都是锐角吗?可以都是直角吗?可以都是钝角吗?
因为两个锐角的和小于180度,所以互为补角的两个角不能都是锐角;
因为两个直角的和等于180度,所以互为补角的两个角可以都是直角;
因为两个钝角的和大于180度,所以互为补角的两个角不能都是钝角;
4.如图,一棵树生长在30°的山坡上,树干与山坡所成的角是多少度?
60°或120°
5.当光线从空气射入水中时,光线的传播方向发生了改变,这就是折射现象(如图,图中的∠1与∠2是对顶角)
∠1与∠2不是对顶角
测试题
C
D
3.
4.一个角的补角比这个角的余角的3倍大10°,求这个角的度数。
解:设这个角是x°
180-x=3(90-x)+10
解得x=50
答:这个角是50°
B
2.1.1两直线的位置关系
一、学习目标
1.在具体情境中了解相交线、平行线、补角、余角、对顶角的定义
2.知道同角或等角的余角相等、同角或等角的补角相等、对顶角相等,
并能解决一些实际问题。
重、难点:补角、余角、对顶角,等角的余角相等、等角的补角相等、
对顶角相等
自主探究:阅读课本p37-40
探究(一)探索在同一平面内,两条直线的位置关系哪两种?
观察下列图片,回答:
结论:
1.一般地,在同一平面内,两条直线的位置关系有两种: 和 .
2.定义分别为:
相交 平行
若两条直线只有一个公共点,称这两条直线相交;
在同一平面内,不相交的两条直线叫做平行线
探究(二)对顶角
(1)概念:有公共 的两个角,如果它们的两边互为 ,这样的两个角就叫做对顶角。
(2)对顶角性质:对顶角 ;
(3)下列各图中,∠1和∠2是对顶角的是( )
顶点
反向延长线
相等
D
探究(三) 3、余角与补角
(1)概念
如果两个角的和是 ,那么称这两个角互为余角;
如果两个角的和是 ,那么称这两个角互为补角。
符号语言:
若∠1+∠2= 90o , 那么∠1与∠2互余。
若∠3+∠4=180o , 那么∠3与∠4互补。
(2)填表:
(3)性质
同角或等角的余角 ;同角或等角的补角 为什么?
90°
180°
相等
相等
(4)练习:如图,∠DON=∠CON=900,∠1=∠2
问题1:哪些角互为补角?哪些角互为余角?
问题2: ∠3与∠4有什么关系?为什么?
理由:∵∠1+∠3=90?,∠2+∠4=90? ∠1=∠2
∴∠3=∠4(同角或等角的余角相等)
问题3:∠AOC与∠BOD有什么关系?为什么?你能仿照问题2写出理由吗?
三.温故知新
直线的基本性质: .
线段的性质: .
两点之间的距离: .
两点确定一条直线
两点之间线段最短
两点之间线段的长度叫做两点之间的距离
四.随堂练习
如图1,∠C=900 则∠A是∠B的 ;
如图2,∠ACB=900 ∠CDA=900 则∠A的余角有哪几个?为什么?
图1
图2
2.∠B,∠ACD
余角
3、如图,直线AB、CD相交于点O,∠AOE=900 ,则
(1)∠1与∠2互为 角; (2)∠1与∠3互为 角;
(3)∠3与∠4互为 角; (4)∠1与∠4互为 角;
(1)补角;(2)对顶角;(3)余角;(4)余角
五.小结:
你还有哪些收获:
哪些疑问:
六.当堂检测:
1、判断:
(1)一个角的余角一定是锐角 ( )
(2)一个角的补角一定是钝角 ( )
(3)若∠1+∠2+∠3=90°,那么∠1、∠2、∠3互为余角 ( )
2、填空:
(1)一个角和它的余角相等,这个角为___________度
(2)一个角和它的补角相等,这个角为__________度
(3)已知∠A=400 ,则∠A的余角是 ,补角是 .
错
对
错
140°
45°
90°
50°
3、下列说法正确的是( )
A.相等的角是对顶角
B.对顶角相等
C.两条直线相交所成的角是对顶角
D.有公共顶点且又相等的角是对顶角
4.如图,直线a,b相交,∠1=35° ,求∠2,∠3,∠4的度数
B
解:因为∠1=35°,
所以∠3= ∠1=35°(对顶角相等)
因为∠1+ ∠2=180°(平角等于180度)
所以∠2=180°-35°=145°
所以∠4= ∠2=145°(对顶角相等)
课后作业:
1.如图,直线a,b相交,∠1=38°,求∠2, ∠3, ,4的度数。
解:因为∠1=38°,
所以∠3= ∠1=38°(对顶角相等)
因为∠1+ ∠2=180°(平角等于180度)
所以∠2=180°-38°=142°
所以∠4= ∠2=142°(对顶角相等)
2.互为补角的两个角可以都是锐角吗?可以都是直角吗?可以都是钝角吗?
因为两个锐角的和小于180度,所以互为补角的两个角不能都是锐角;
因为两个直角的和等于180度,所以互为补角的两个角可以都是直角;
因为两个钝角的和大于180度,所以互为补角的两个角不能都是钝角;
4.如图,一棵树生长在30°的山坡上,树干与山坡所成的角是多少度?
60°或120°
5.当光线从空气射入水中时,光线的传播方向发生了改变,这就是折射现象(如图,图中的∠1与∠2是对顶角)
∠1与∠2不是对顶角
测试题
C
D
3.
4.一个角的补角比这个角的余角的3倍大10°,求这个角的度数。
解:设这个角是x°
180-x=3(90-x)+10
解得x=50
答:这个角是50°
B
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
