北师大版七年级数学下册课件:1.1同底数幂的乘法(共17张PPT)
文档属性
| 名称 | 北师大版七年级数学下册课件:1.1同底数幂的乘法(共17张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 00:00:00 | ||
图片预览







文档简介
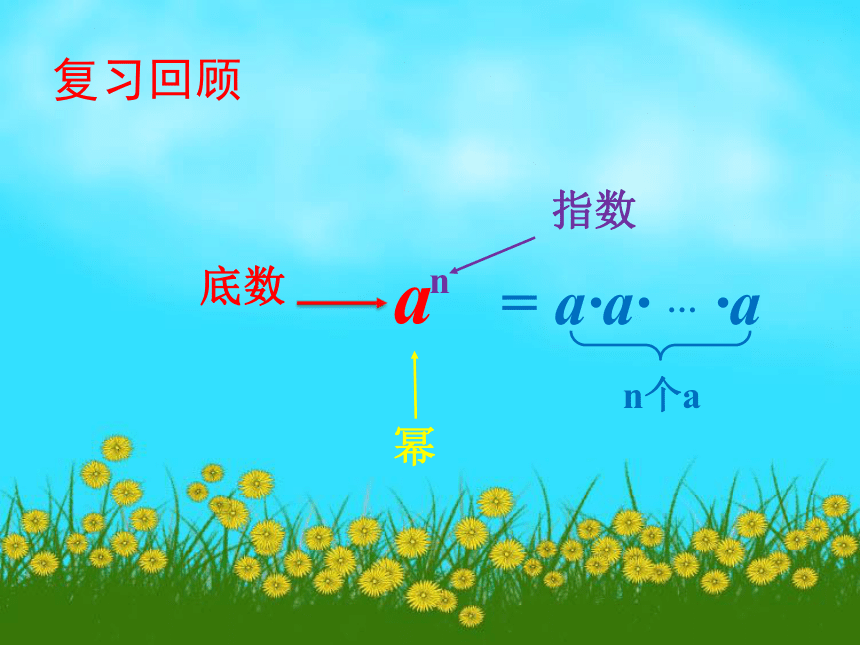
复习回顾
a
n
指数
幂
= a·a· … ·a
n个a
底数
第一章 整式的乘除
1 同底数幂的乘法
龙山学校
学习目标
1、理解同底数幂的乘法法则的由来,掌握同底数幂相乘的乘法法则;
2、学会并熟练地运用同底数幂的乘法法则进行计算;
自学指导
认真看课本P2--- P3练习前面,注意:
1、解答P2“议一议”中的问题,理解同底数幂的乘法法则的推导过程.
2、 注意例题1的解题格式和步骤.
5分钟后,比谁能正确地做出与例题类似的检测题.(P2做一做)
议一议
am · an等于什么(m,n都是正整数)?为什么?
=am+n
am · an =am+n(m,n都是正整数)
不变
相加
议一议
同底数幂相乘,底数 ,指数 .
底数不变
指数相加
不变
相加
自学指导
认真看课本P2--- P3练习前面,注意:
1、解答P2“议一议”中的问题,理解同底数幂的乘法法则的推导过程.
2、 注意例题1的解题格式和步骤.
5分钟后,比谁能正确地做出与例题类似的检测题.(P2做一做)
巩固落实
做一做
1.计算下列各式:
(1)102×103;
(2)105×108;
(3)10m×10n(m,n都是正整数).
你发现了什么?
2. 2m×2n等于什么? 呢?
(-3)m×(-3)n呢?(m,n 都是正整数)
这个结论是否具有一般性?如果底数同样也是字母呢?
应用提高
am · an · ap 等于什么?
am· an· ap = am+n+p
你是怎样做的?与同伴交流
应用提高
判断(正确的打“√”,错误的打“×”)
x4·x6=x24 ( ) (2) x·x3=x3 ( )
(3) x4+x4=x8 ( ) (4) x2·x2=2x4 ( )
(5)(-x)2 · (-x)3 = (-x)5 ( )
(6)a2·a3- a3·a2 = 0 ( )
(7)x3·y5=(xy)8 ( )
(8) x7+x7=x14 ( )
√
√
×
×
×
×
×
×
对于计算出错的题目,你能分析出错的原因吗?试试看!
应用提高
例2 光在真空中的速度约为3×108m/s,太阳光照射到地球大约需要5×102s. 地球距离太阳大约有多远?
解: 3×108×5×102
=15×1010
=1.5×1011(m)
地球距离太阳大约有1.5×1011m.
应用提高
1.计算:
(1)52×57; (2)7×73×72;
(3)-x2·x3; (4)(-c)3·(-c)m.
2.一种电子计算机每秒可做4×109次运算,它工作5×102s可做多少次运算?
3.解决本节课一开始比邻星到地球的距离问题.
这四道题是什么运算?为什么?
拓展延伸
把下列各式写成幂的形式
小结
小结:
1、am·an=am+n(m,n都是正整数)
同底数幂相乘,底数 不变 ,指数 相加
2、指数也可以是多项式. Xm-1·xm+1
3、底数也可以是多项式. (2a+1)5·(2a+1)3
作业
完成课本习题1.1中所有习题
拓展作业:
你能尝试运用今天所学的同底数幂的乘法解决下面的问题吗
a
n
指数
幂
= a·a· … ·a
n个a
底数
第一章 整式的乘除
1 同底数幂的乘法
龙山学校
学习目标
1、理解同底数幂的乘法法则的由来,掌握同底数幂相乘的乘法法则;
2、学会并熟练地运用同底数幂的乘法法则进行计算;
自学指导
认真看课本P2--- P3练习前面,注意:
1、解答P2“议一议”中的问题,理解同底数幂的乘法法则的推导过程.
2、 注意例题1的解题格式和步骤.
5分钟后,比谁能正确地做出与例题类似的检测题.(P2做一做)
议一议
am · an等于什么(m,n都是正整数)?为什么?
=am+n
am · an =am+n(m,n都是正整数)
不变
相加
议一议
同底数幂相乘,底数 ,指数 .
底数不变
指数相加
不变
相加
自学指导
认真看课本P2--- P3练习前面,注意:
1、解答P2“议一议”中的问题,理解同底数幂的乘法法则的推导过程.
2、 注意例题1的解题格式和步骤.
5分钟后,比谁能正确地做出与例题类似的检测题.(P2做一做)
巩固落实
做一做
1.计算下列各式:
(1)102×103;
(2)105×108;
(3)10m×10n(m,n都是正整数).
你发现了什么?
2. 2m×2n等于什么? 呢?
(-3)m×(-3)n呢?(m,n 都是正整数)
这个结论是否具有一般性?如果底数同样也是字母呢?
应用提高
am · an · ap 等于什么?
am· an· ap = am+n+p
你是怎样做的?与同伴交流
应用提高
判断(正确的打“√”,错误的打“×”)
x4·x6=x24 ( ) (2) x·x3=x3 ( )
(3) x4+x4=x8 ( ) (4) x2·x2=2x4 ( )
(5)(-x)2 · (-x)3 = (-x)5 ( )
(6)a2·a3- a3·a2 = 0 ( )
(7)x3·y5=(xy)8 ( )
(8) x7+x7=x14 ( )
√
√
×
×
×
×
×
×
对于计算出错的题目,你能分析出错的原因吗?试试看!
应用提高
例2 光在真空中的速度约为3×108m/s,太阳光照射到地球大约需要5×102s. 地球距离太阳大约有多远?
解: 3×108×5×102
=15×1010
=1.5×1011(m)
地球距离太阳大约有1.5×1011m.
应用提高
1.计算:
(1)52×57; (2)7×73×72;
(3)-x2·x3; (4)(-c)3·(-c)m.
2.一种电子计算机每秒可做4×109次运算,它工作5×102s可做多少次运算?
3.解决本节课一开始比邻星到地球的距离问题.
这四道题是什么运算?为什么?
拓展延伸
把下列各式写成幂的形式
小结
小结:
1、am·an=am+n(m,n都是正整数)
同底数幂相乘,底数 不变 ,指数 相加
2、指数也可以是多项式. Xm-1·xm+1
3、底数也可以是多项式. (2a+1)5·(2a+1)3
作业
完成课本习题1.1中所有习题
拓展作业:
你能尝试运用今天所学的同底数幂的乘法解决下面的问题吗
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
