北师大版七年级数学下册课件:1.2.1幂的乘方(共15张PPT)
文档属性
| 名称 | 北师大版七年级数学下册课件:1.2.1幂的乘方(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 12:51:15 | ||
图片预览

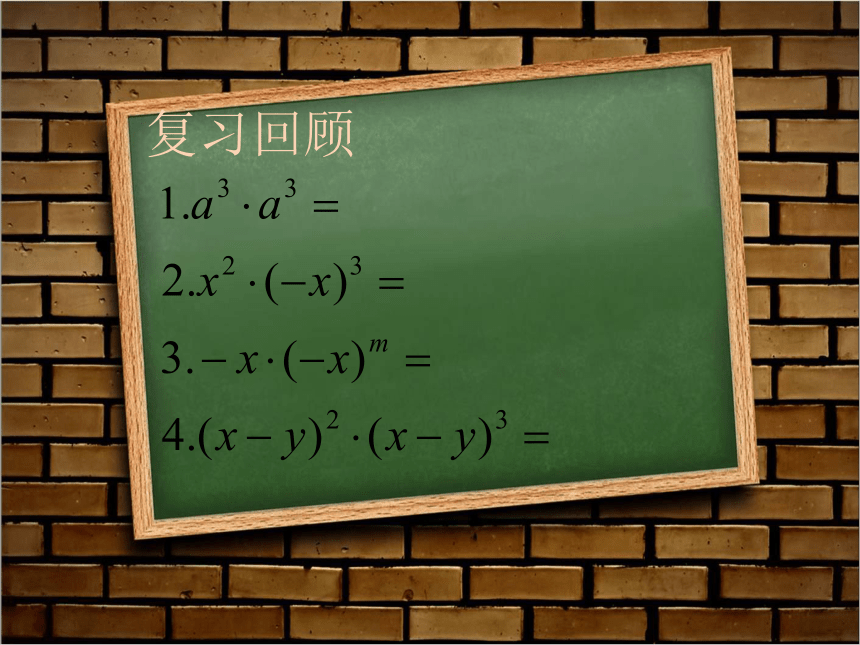





文档简介
复习回顾
同底数幂乘法的运算性质:
am · an
=(a·a· … ·a)
m个a
= a·a· … ·a
(m+n)个a
= am+n
am·an= am+n
a·a· … ·a
n个a
an
幂的意义:
=
同底数幂相乘,底数不变,指数相加.
· (a·a· … ·a)
n个a
复习回顾
第一章 整式的乘除
1.2.1幂的乘方
【学习目标】
1、理解幂的乘方的性质.
2、能准确地运用幂的乘方性质进行计算.
自学指导
认真看课本P5--- P6练习前面.注意:
1、解答P5“做一做”中的问题,理解幂的乘方性质的推导过程.
2、看P6例1是如何运用幂的乘方的性质?
6分钟后,比谁能正确地做出与例题类似的检测题 .
情境引入
地球、木星、太阳可以近似地看做是球体 .木星、太阳的半径分别约是地球的10倍和102倍,它们的体积分别约是地球的多少倍?
V球= —πr3 ,
其中V是体积、r是球的半径
3
4
103倍
(102)3倍
探究新知
你知道(102)3等于多少吗?
(102)3
=102×102×102
=102+2+2
=102×3
=106
(根据 ).
(根据 ).
同底数幂的乘法
幂的意义
个am
=am·am· … ·am
探究新知
做一做:计算下列各式,并说明理由 .
(1) (62)4 ; (2) (a2)3 ; (3) (am)2 ; (4) (am)n .
解:(1) (62)4
(2) (a2)3
(3) (am)2
= 62·62· 62·62
=62+2+2+2
=68
= a2·a2·a2
=a2+2+2
=a6
=am·am
=am+m
=62×4 ;
(62)4
=a2×3 ;
(a2)3
=a2m ;
(am)2
n
(4) (am)n
=amn
个m
=am+m+ … +m
n
探究新知
幂的乘方,底数 ,指数 .
(am)n=amn (m,n都是正整数)
不变
相乘
幂的乘方法则
落实基础
例1 计算:
(102)3 ; (2) (b5)5 ;
(an)3; (4) -(x2)m ;
(5) (y2)3 · y ; (6) 2(a2)6 - (a3)4 .
当堂训练
2. 计算:
(1) (103)3 ; (2) -(a2)5 ; (3) (x3)4 · x2 ;
(4) [(-x)2 ]3 ; (5) (-a)2(a2)2; (6) x·x4 – x2 · x3 .
随堂练习:
1. 判断下面计算是否正确?如果有错误请改正:
(1) (x3)3 = x6 ; (2)a6 · a4 = a24 .
联系拓广
⑴ a12 =(a3)( ) =(a2)( )
=a3 a( )=( )3 =( )4
(4) 32﹒9m =3( )
(2) y3n =3, y9n = .
(3) (a2)m+1 = .
小结
1.
同底数幂相乘,底数不变,指数相加.
2.
(am)n=amn (m,n都是正整数)
幂的乘方,底数不变,指数相乘.
作业
完成课本习题1.2中1、2
拓展作业:
你能尝试运用今天所学的知识解决下面的问题吗
(1)填空: [(a-b)3 ]2=(b-a )( )
(2)若4﹒8m﹒16m =29 , 求m的值
(1).[ (-m)3]4
(2).(a3-m)2
(3).(-x3) 2 ·(-x2 )3
(4).( tm) 2 · t
(5). (a3)2 · (a2 )3
(6).2(x3) 4 + x4· (x4) 2 + x5 · x7 + x6 · (x3)2
同底数幂乘法的运算性质:
am · an
=(a·a· … ·a)
m个a
= a·a· … ·a
(m+n)个a
= am+n
am·an= am+n
a·a· … ·a
n个a
an
幂的意义:
=
同底数幂相乘,底数不变,指数相加.
· (a·a· … ·a)
n个a
复习回顾
第一章 整式的乘除
1.2.1幂的乘方
【学习目标】
1、理解幂的乘方的性质.
2、能准确地运用幂的乘方性质进行计算.
自学指导
认真看课本P5--- P6练习前面.注意:
1、解答P5“做一做”中的问题,理解幂的乘方性质的推导过程.
2、看P6例1是如何运用幂的乘方的性质?
6分钟后,比谁能正确地做出与例题类似的检测题 .
情境引入
地球、木星、太阳可以近似地看做是球体 .木星、太阳的半径分别约是地球的10倍和102倍,它们的体积分别约是地球的多少倍?
V球= —πr3 ,
其中V是体积、r是球的半径
3
4
103倍
(102)3倍
探究新知
你知道(102)3等于多少吗?
(102)3
=102×102×102
=102+2+2
=102×3
=106
(根据 ).
(根据 ).
同底数幂的乘法
幂的意义
个am
=am·am· … ·am
探究新知
做一做:计算下列各式,并说明理由 .
(1) (62)4 ; (2) (a2)3 ; (3) (am)2 ; (4) (am)n .
解:(1) (62)4
(2) (a2)3
(3) (am)2
= 62·62· 62·62
=62+2+2+2
=68
= a2·a2·a2
=a2+2+2
=a6
=am·am
=am+m
=62×4 ;
(62)4
=a2×3 ;
(a2)3
=a2m ;
(am)2
n
(4) (am)n
=amn
个m
=am+m+ … +m
n
探究新知
幂的乘方,底数 ,指数 .
(am)n=amn (m,n都是正整数)
不变
相乘
幂的乘方法则
落实基础
例1 计算:
(102)3 ; (2) (b5)5 ;
(an)3; (4) -(x2)m ;
(5) (y2)3 · y ; (6) 2(a2)6 - (a3)4 .
当堂训练
2. 计算:
(1) (103)3 ; (2) -(a2)5 ; (3) (x3)4 · x2 ;
(4) [(-x)2 ]3 ; (5) (-a)2(a2)2; (6) x·x4 – x2 · x3 .
随堂练习:
1. 判断下面计算是否正确?如果有错误请改正:
(1) (x3)3 = x6 ; (2)a6 · a4 = a24 .
联系拓广
⑴ a12 =(a3)( ) =(a2)( )
=a3 a( )=( )3 =( )4
(4) 32﹒9m =3( )
(2) y3n =3, y9n = .
(3) (a2)m+1 = .
小结
1.
同底数幂相乘,底数不变,指数相加.
2.
(am)n=amn (m,n都是正整数)
幂的乘方,底数不变,指数相乘.
作业
完成课本习题1.2中1、2
拓展作业:
你能尝试运用今天所学的知识解决下面的问题吗
(1)填空: [(a-b)3 ]2=(b-a )( )
(2)若4﹒8m﹒16m =29 , 求m的值
(1).[ (-m)3]4
(2).(a3-m)2
(3).(-x3) 2 ·(-x2 )3
(4).( tm) 2 · t
(5). (a3)2 · (a2 )3
(6).2(x3) 4 + x4· (x4) 2 + x5 · x7 + x6 · (x3)2
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
