北师大版七年级下册 1.5平方差公式教学 课件 共16张PPT)
文档属性
| 名称 | 北师大版七年级下册 1.5平方差公式教学 课件 共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 336.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 00:00:00 | ||
图片预览





文档简介
课前基础测评
计算:
1、①、4x2.6x3=
②、
5a3.4ab=
,
2、①、2a2(a-b+1)=
②、-2xy(x2-2x-1)=
,
3、计算,写出简单过程:
①、(2x+3)(2x-3)
②、(x+2y)(x
-
2y)
1、①、4x2.6x3=
24x5
②、
5a3.4ab=
20a4b
,
2、①、2a2(a-b+1)=
2a3-2a2b+2a2
②、-2xy(x2-2x-1)=
-2x3y+2x2y+2xy
,
3、计算,写出简单过程:
①、(2x+3)(2x-3)
解:原式=4x2-6x+6x-9=4x2-9
②、(x+2y)(x
-
2y)
解:原式=x2-2xy+2xy-4y2=x2-4y2
课前基础测评
平方差公式
平方差公式的特征探讨:
?
1、请同学们阅读书P20页的内容;
2、请同学们思考三个问题:
①、如何推导?
②
、什么情况下可用这一公式?
③、怎样用?
平方差公式
平方差公式的几何背景:
首先回忆我们曾经用
几何的意义即图形面积来解释整式乘法
运算法则,如:a(b+c)=ab+ac;
平方差公式
平方差公式的几何背景:
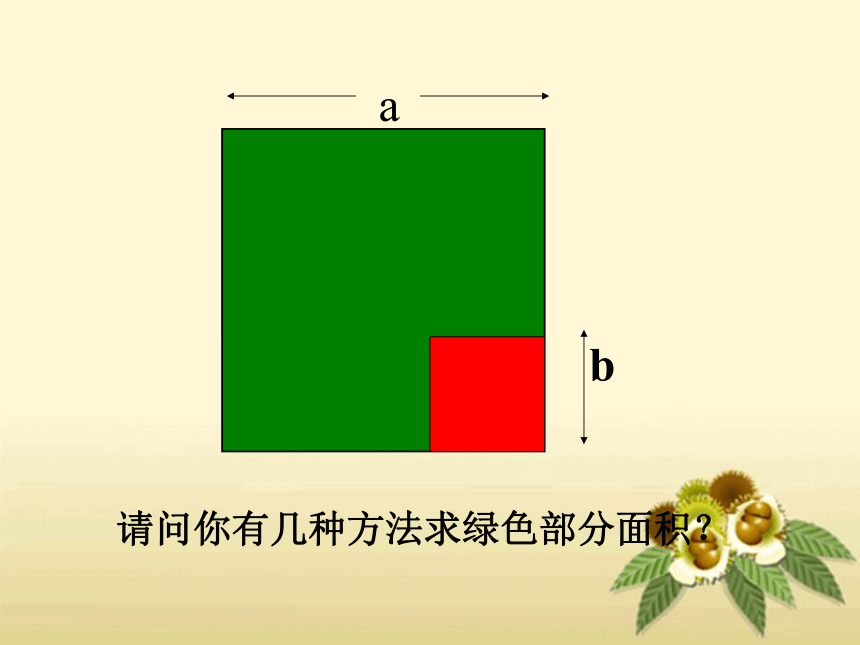
请同学们思考如何用几何图形的面积来解释(a
+b)(a-b)呢?
1、当a>b>0时,我们可能看成是以长为(a+b)
,
宽为(a-b)的长方形的面积.
2、如何解释公式的右端a2
–
b2.
b
a
请问你有几种方法求绿色部分面积?
?
?
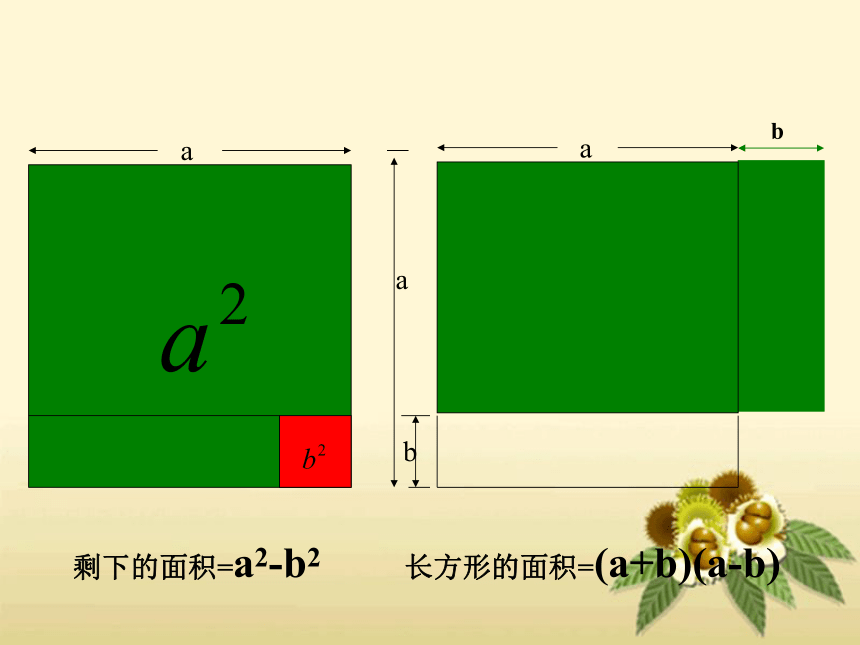
a
b
a
长方形的面积=(a+b)(a-b)
剩下的面积=a2-b2
a
b
平方差公式
1、结论:(a+b)(a-b)=
a2
–
b2
两数的和与它们的差的积,等于这两数的平方差.
2、观察平方差公式的
变式情形:
(a-b)(a+b)=a2–b2
(-a+b)(-a-b)=
a2
–
b2
(b+
a)(-b
+
a)=
a2
–
b2
(b+
a)(a-b)=
a2
–
b2
3、特点分析:
①、有两个数是完全相同的,有两个数是相反的;
重点是观察它们的符号.
②、结果是这两数的平方差,但要注意是谁的平方减去谁的平方,符号相同数的平方减去符号不同数的平方;
平方差公式法则的应用:
1、例题的处理办法:
①
、鼓励学生尝试独立完成;
②、个别学生相对弱的,老师指引;
③、对例题进行变式训练:
平方差公式
2、例题的变式训练:
(2a+3b)(2a-3b)
(-2a+3b)(-2a-3b)
(3b+2a)(2a-3b)
(-2a-3b)(2a-3b)
3、利用平方差公式计算:1998×2002
技巧小结:如何找符合公式(a+b)(a-b)的a和b
例1
利用平方差公式计算:
(1)(7+6x)(7?6x);
(2)(3y
+
x)(x?3y);
(3)(?m+2n)(?m?2n).
解:(1)
(7+6x)(7?6x)=
(2)(3y+x)
(x?3y)
=
(3)(?m+2n)(?m?2n
)
72-(6x)2=
49-36x2
x2-3y2=
x2-9y2
=(-m)2-(2n)2
=m2-4n2
(1)1992×2008
(1)1992×2008
=(2000
?8)
×(2000+8
)
=20002
?82
=4000000?64
=3
999
936
例2
利用平方差公式计算:
解:
(2)996×1004
(2)996×1004
=(1000
?4)
×(1000+4
)
=10002
?42
=1000000?16
=999
984
平方差公式
分层练习:
A组:判断下列多项式乘法中,哪些可以用平方差公式来计算.
1、(x-2y)(x+2y)
(
)
2、(a-2b)(-a-2b)
(
)
3、(-2m-n)(n
+
2m)
(
)
4、(2c-b)(
-b-2c)
(
)
B组:1、计算:
(2x+
)(2x-
)
(-x+2)(-x-2)
?
(-2x+y)(2x+y)
(y-x)(-x-y)
2、简便计算:
?(1)498×502
(2)999×1001
C组:
1、(x-1)(x2
+1)(x+1)
2、(a-3)(a+4)(a+3)(a-4)
?
3、(2a-5b)(2a+5b)(4a2+25b2)
4、20042-2005×2003
平方差公式
一、判断下列多项式乘法中,哪些可以用平方差公式来计算.
1、(x-2y)(x+2y)
(
)
2、(a-2b)(-a-2b)
(
)
3、(-2m-n)(n
+
2m)
(
)
4、(2c-b)(
-b-2c)
(
)
二、计算:
1、(2a+
)
(2a-
)
三、简便计算:1、
497×503
2、
998×1002
2、(-b+2)(-b-2);
3、(-2a+b)(2a+b);
4、(a-b)(-a-b)
平方差公式
课堂练方差公式
课外拓展:
计算(用指数形式表示)
1、(x-1)(x+1)
(x2+1)(x4+1)
(x8+1)
(x16+1)
?
2、(2+1)
(22+1)(24+1)
(28+1)
(216+1)
?
3、(x+1)
(x2+1)(x4+1)
(x8+1)
(x16+1)
作业:
P21
习题1.9
补充题:计算1、10.3×9.7
2、
课堂小结:
1、知识点小结:引导学生与老师、学生与学生讨论
本节课所学的知识以及在应用平方差公式解题时应把握
的要点.
2、学生自身能力方面,注意自身观察力的培养、注
重解题技巧的形成.
计算:
1、①、4x2.6x3=
②、
5a3.4ab=
,
2、①、2a2(a-b+1)=
②、-2xy(x2-2x-1)=
,
3、计算,写出简单过程:
①、(2x+3)(2x-3)
②、(x+2y)(x
-
2y)
1、①、4x2.6x3=
24x5
②、
5a3.4ab=
20a4b
,
2、①、2a2(a-b+1)=
2a3-2a2b+2a2
②、-2xy(x2-2x-1)=
-2x3y+2x2y+2xy
,
3、计算,写出简单过程:
①、(2x+3)(2x-3)
解:原式=4x2-6x+6x-9=4x2-9
②、(x+2y)(x
-
2y)
解:原式=x2-2xy+2xy-4y2=x2-4y2
课前基础测评
平方差公式
平方差公式的特征探讨:
?
1、请同学们阅读书P20页的内容;
2、请同学们思考三个问题:
①、如何推导?
②
、什么情况下可用这一公式?
③、怎样用?
平方差公式
平方差公式的几何背景:
首先回忆我们曾经用
几何的意义即图形面积来解释整式乘法
运算法则,如:a(b+c)=ab+ac;
平方差公式
平方差公式的几何背景:
请同学们思考如何用几何图形的面积来解释(a
+b)(a-b)呢?
1、当a>b>0时,我们可能看成是以长为(a+b)
,
宽为(a-b)的长方形的面积.
2、如何解释公式的右端a2
–
b2.
b
a
请问你有几种方法求绿色部分面积?
?
?
a
b
a
长方形的面积=(a+b)(a-b)
剩下的面积=a2-b2
a
b
平方差公式
1、结论:(a+b)(a-b)=
a2
–
b2
两数的和与它们的差的积,等于这两数的平方差.
2、观察平方差公式的
变式情形:
(a-b)(a+b)=a2–b2
(-a+b)(-a-b)=
a2
–
b2
(b+
a)(-b
+
a)=
a2
–
b2
(b+
a)(a-b)=
a2
–
b2
3、特点分析:
①、有两个数是完全相同的,有两个数是相反的;
重点是观察它们的符号.
②、结果是这两数的平方差,但要注意是谁的平方减去谁的平方,符号相同数的平方减去符号不同数的平方;
平方差公式法则的应用:
1、例题的处理办法:
①
、鼓励学生尝试独立完成;
②、个别学生相对弱的,老师指引;
③、对例题进行变式训练:
平方差公式
2、例题的变式训练:
(2a+3b)(2a-3b)
(-2a+3b)(-2a-3b)
(3b+2a)(2a-3b)
(-2a-3b)(2a-3b)
3、利用平方差公式计算:1998×2002
技巧小结:如何找符合公式(a+b)(a-b)的a和b
例1
利用平方差公式计算:
(1)(7+6x)(7?6x);
(2)(3y
+
x)(x?3y);
(3)(?m+2n)(?m?2n).
解:(1)
(7+6x)(7?6x)=
(2)(3y+x)
(x?3y)
=
(3)(?m+2n)(?m?2n
)
72-(6x)2=
49-36x2
x2-3y2=
x2-9y2
=(-m)2-(2n)2
=m2-4n2
(1)1992×2008
(1)1992×2008
=(2000
?8)
×(2000+8
)
=20002
?82
=4000000?64
=3
999
936
例2
利用平方差公式计算:
解:
(2)996×1004
(2)996×1004
=(1000
?4)
×(1000+4
)
=10002
?42
=1000000?16
=999
984
平方差公式
分层练习:
A组:判断下列多项式乘法中,哪些可以用平方差公式来计算.
1、(x-2y)(x+2y)
(
)
2、(a-2b)(-a-2b)
(
)
3、(-2m-n)(n
+
2m)
(
)
4、(2c-b)(
-b-2c)
(
)
B组:1、计算:
(2x+
)(2x-
)
(-x+2)(-x-2)
?
(-2x+y)(2x+y)
(y-x)(-x-y)
2、简便计算:
?(1)498×502
(2)999×1001
C组:
1、(x-1)(x2
+1)(x+1)
2、(a-3)(a+4)(a+3)(a-4)
?
3、(2a-5b)(2a+5b)(4a2+25b2)
4、20042-2005×2003
平方差公式
一、判断下列多项式乘法中,哪些可以用平方差公式来计算.
1、(x-2y)(x+2y)
(
)
2、(a-2b)(-a-2b)
(
)
3、(-2m-n)(n
+
2m)
(
)
4、(2c-b)(
-b-2c)
(
)
二、计算:
1、(2a+
)
(2a-
)
三、简便计算:1、
497×503
2、
998×1002
2、(-b+2)(-b-2);
3、(-2a+b)(2a+b);
4、(a-b)(-a-b)
平方差公式
课堂练方差公式
课外拓展:
计算(用指数形式表示)
1、(x-1)(x+1)
(x2+1)(x4+1)
(x8+1)
(x16+1)
?
2、(2+1)
(22+1)(24+1)
(28+1)
(216+1)
?
3、(x+1)
(x2+1)(x4+1)
(x8+1)
(x16+1)
作业:
P21
习题1.9
补充题:计算1、10.3×9.7
2、
课堂小结:
1、知识点小结:引导学生与老师、学生与学生讨论
本节课所学的知识以及在应用平方差公式解题时应把握
的要点.
2、学生自身能力方面,注意自身观察力的培养、注
重解题技巧的形成.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
