北师大版七年级下册 2.1 两条直线的位置关系 课件(共22张PPT)
文档属性
| 名称 | 北师大版七年级下册 2.1 两条直线的位置关系 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 15:41:14 | ||
图片预览


文档简介
第二章 相交线与平行线
1 两条直线的位置关系
观察下面的几幅生活中的图片,想想两条直线的位置关系都有哪两种?
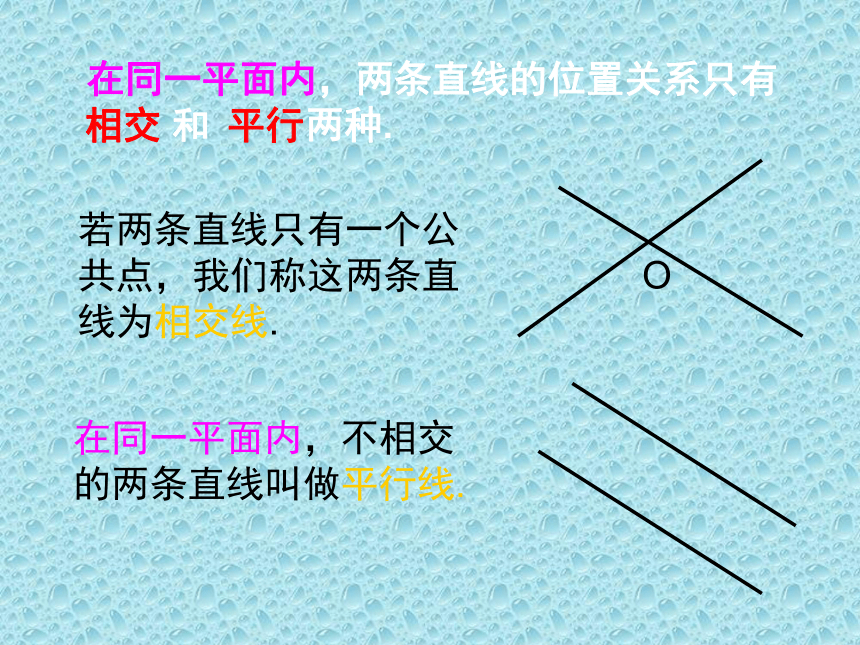
若两条直线只有一个公共点,我们称这两条直线为相交线.
O
在同一平面内,不相交的两条直线叫做平行线.
在同一平面内,两条直线的位置关系只有
和 两种.
相交
平行
m
n
a
b
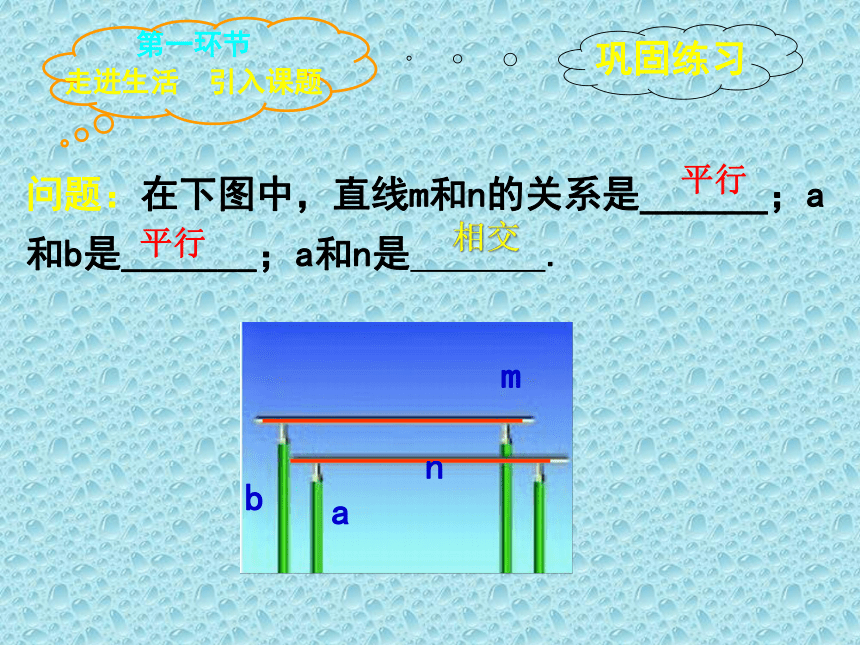
问题:在下图中,直线m和n的关系是______;a和b是_______;a和n是 .
巩固练习
第一环节
走进生活 引入课题
平行
平行
相交
特别提醒
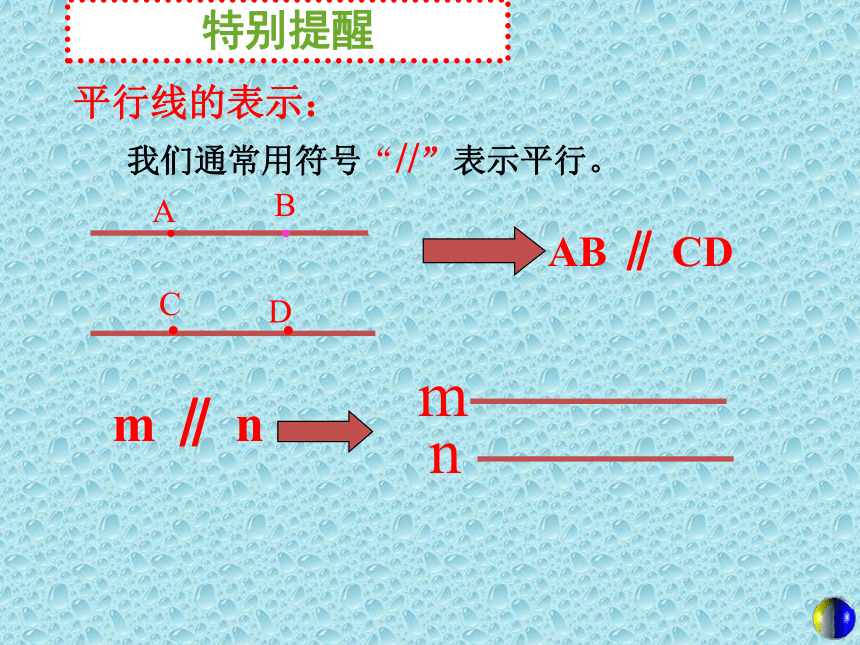
我们通常用符号“//”表示平行。
平行线的表示:
C
D
B
A
·
·
·
·
m ∥ n
AB ∥ CD
m
n
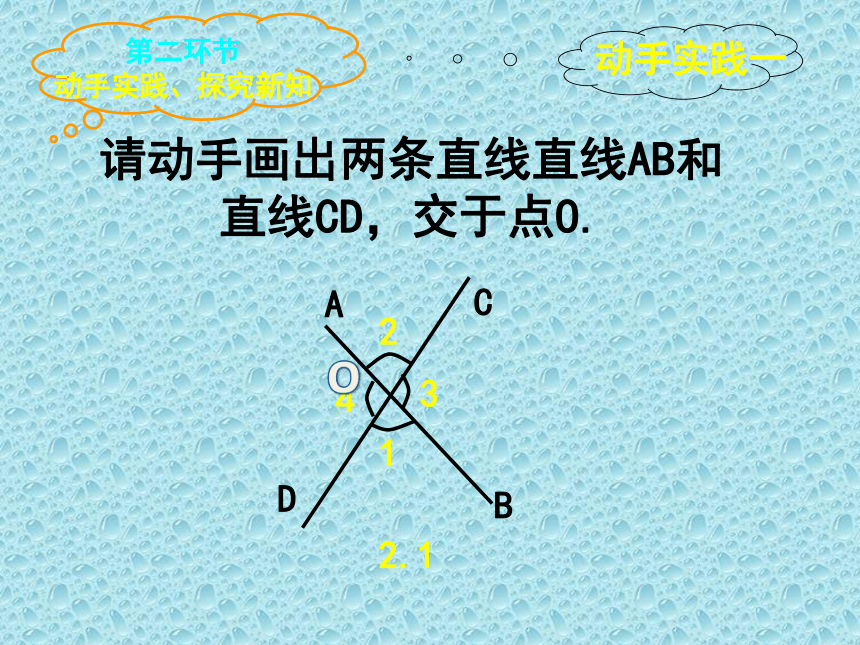
请动手画出两条直线直线AB和直线CD,交于点O.
3
2
1
4
2.1
A
B
C
D
动手实践一
第二环节
动手实践、探究新知
o
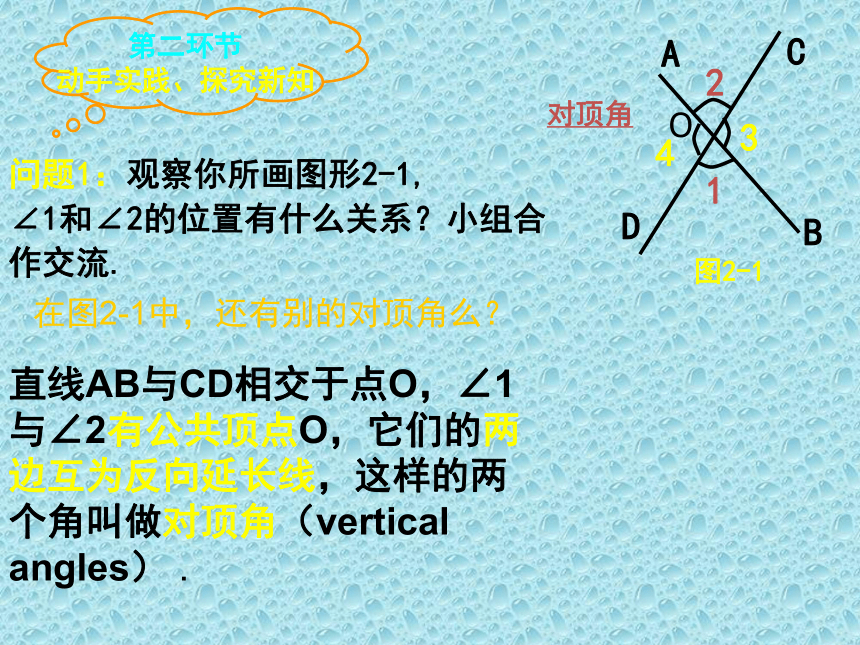
问题1:观察你所画图形2-1,
∠1和∠2的位置有什么关系?小组合作交流.
3
2
1
4
图2-1
A
B
C
D
第二环节
动手实践、探究新知
对顶角
在图2-1中,还有别的对顶角么?
直线AB与CD相交于点O,∠1与∠2有公共顶点O,它们的两边互为反向延长线,这样的两个角叫做对顶角(vertical angles) .
O
1
2
3
4
B
C
D
o
A
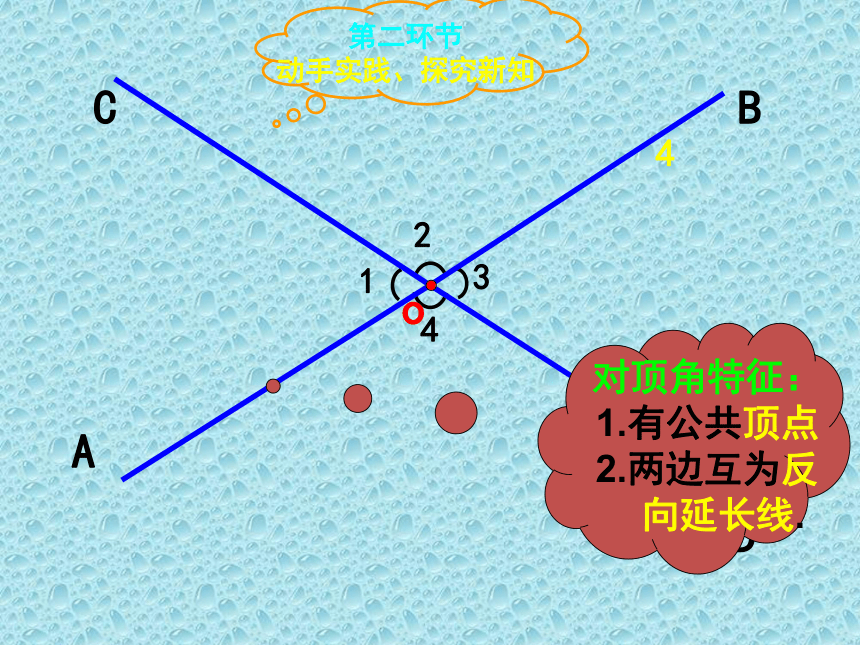
对顶角特征:
1.有公共顶点
2.两边互为反
向延长线.
4
第二环节
动手实践、探究新知
归纳总结
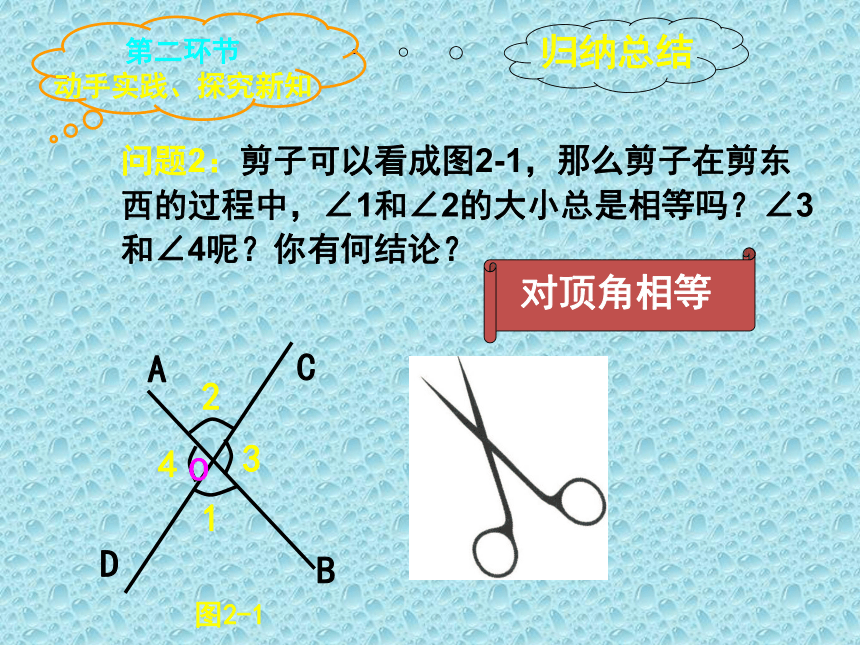
对顶角相等
第二环节
动手实践、探究新知
问题2:剪子可以看成图2-1,那么剪子在剪东西的过程中,∠1和∠2的大小总是相等吗?∠3和∠4呢?你有何结论?
3
2
1
4
图2-1
A
B
C
D
O
1
2
1
2
1
2
1
2
A
B
C
D
1.下列各图中,∠1和∠2是对顶角的是( )
2.如右图所示,有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数吗?你能说出所量角的度数是多少吗?为什么?
D
巩固练习
第二环节
动手实践、探究新知
如果两个角的和是1800,那么称这两个角互为补角.
如果两个角的和是900,那么称这两个角互为余角.
注意:互余与互补是指两个角之间的数量关系,与它们的位置无关.
第二环节
动手实践、探究新知
3
4
A
D
问题3:在右图中,∠1与∠3有什么数量关系?图2.4中∠A和∠B有什么数量关系?
2
1
O
B
C
∠1+∠3=180°
∠A+∠B=90°
第二环节
动手实践、探究新知
判断:下列说法正确的有 .(填序号)
①若∠1+∠2+∠3=180?,则∠1、∠2、∠3互补
②若∠A=40?26′,则∠A的余角=49?34′
③一个角的补角必为钝角.
②
第二环节
动手实践、探究新知
2
1
O
B
C
A
D
3
4
第二环节
动手实践、探究新知
图1
1.图1中∠1 与∠3 ,∠2与∠3有什么关系;
2.图2.1-10中∠A与∠B ,∠A与∠ACD有什么关系?
答:
1: ∠1 与∠3 互为补交,∠2与∠3互为补交
2: ∠A与∠B互为余角 ,∠A与∠ACD互为余角
3:∠1和∠2有什么关系? ∠B和∠ACD有什么关系?
答:∠1=∠2 ∠B=∠ACD
同角或等角的补角相等
归纳总结
同角或等角的余角相等
问题1:
①.因为∠1+∠2=90?,∠2+∠3=90?,所以∠1= ,理由是
② 因为∠1+∠2=180?,∠2+∠3=180?,所以∠1= ,理由是
巩固练习
第三环节
学以致用,步步为营
∠3
同角或等角的余角相等
同角或等角的补角相等
∠3
问题2:如图2.1—11已知:直线AB与CD交于点O, ∠EOD=900,回答下列问题:
1.∠AOE的余角是 ;补角是. _ __
2.∠AOC的余角是__ ;补角是 ;对顶角是 ___.
巩固练习
C
A
B
D
O
E
2.1─11
第三环节
学以致用,步步为营
∠AOC或∠BOD
∠EOB
∠AOE___
∠AOD_或∠COB__
∠BOD
问题2:①你手中的三角板,如图2-4.则∠A是∠B的 .
变式训练:在①的基础上,做∠CDA=900.
1.则∠A的余角有哪几个?为什么?
2.请找出互补的角,并说明理由.
巩固练习
C
A
B
2.4
C
A
B
2.1─10
D
第四环节
拓展延伸,综合应用
余角
例1、如图,直线a、b相交,∠1=40°,求 ∠2、∠3、∠4的度数。
学以致用:
a
b
)
(
1
3
4
2
)
(
解:由邻补角的定义可知
∠2=180°-∠1
=180°-40°=140°
由对顶角相等可得
∠3=∠1=40°,∠4=∠2=140°
变式:直线AB、CD相交与点O,∠AOC=40°,OE平分∠AOC,求∠DOE的度数。
A
B
O
C
D
E
解:∵OE平分∠AOC, 且∠AOC =40°
∴∠COE= ∠AOC=20°
∵∠DOE与∠COE互为补角
∴∠DOE=180°-∠COE=120°
因此∠DOE=120°
你学到了哪些知识?
第五环节
学有所思,反馈巩固
一、定义:
1、对顶角
2、互为补角,互为余角
二、性质:
对顶角相等
同角或等角的余角相等
同角或等角的补角相等
作业:
课本40页
习题2.1的1;2
第六环节
布置作业,能力延伸
1 两条直线的位置关系
观察下面的几幅生活中的图片,想想两条直线的位置关系都有哪两种?
若两条直线只有一个公共点,我们称这两条直线为相交线.
O
在同一平面内,不相交的两条直线叫做平行线.
在同一平面内,两条直线的位置关系只有
和 两种.
相交
平行
m
n
a
b
问题:在下图中,直线m和n的关系是______;a和b是_______;a和n是 .
巩固练习
第一环节
走进生活 引入课题
平行
平行
相交
特别提醒
我们通常用符号“//”表示平行。
平行线的表示:
C
D
B
A
·
·
·
·
m ∥ n
AB ∥ CD
m
n
请动手画出两条直线直线AB和直线CD,交于点O.
3
2
1
4
2.1
A
B
C
D
动手实践一
第二环节
动手实践、探究新知
o
问题1:观察你所画图形2-1,
∠1和∠2的位置有什么关系?小组合作交流.
3
2
1
4
图2-1
A
B
C
D
第二环节
动手实践、探究新知
对顶角
在图2-1中,还有别的对顶角么?
直线AB与CD相交于点O,∠1与∠2有公共顶点O,它们的两边互为反向延长线,这样的两个角叫做对顶角(vertical angles) .
O
1
2
3
4
B
C
D
o
A
对顶角特征:
1.有公共顶点
2.两边互为反
向延长线.
4
第二环节
动手实践、探究新知
归纳总结
对顶角相等
第二环节
动手实践、探究新知
问题2:剪子可以看成图2-1,那么剪子在剪东西的过程中,∠1和∠2的大小总是相等吗?∠3和∠4呢?你有何结论?
3
2
1
4
图2-1
A
B
C
D
O
1
2
1
2
1
2
1
2
A
B
C
D
1.下列各图中,∠1和∠2是对顶角的是( )
2.如右图所示,有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数吗?你能说出所量角的度数是多少吗?为什么?
D
巩固练习
第二环节
动手实践、探究新知
如果两个角的和是1800,那么称这两个角互为补角.
如果两个角的和是900,那么称这两个角互为余角.
注意:互余与互补是指两个角之间的数量关系,与它们的位置无关.
第二环节
动手实践、探究新知
3
4
A
D
问题3:在右图中,∠1与∠3有什么数量关系?图2.4中∠A和∠B有什么数量关系?
2
1
O
B
C
∠1+∠3=180°
∠A+∠B=90°
第二环节
动手实践、探究新知
判断:下列说法正确的有 .(填序号)
①若∠1+∠2+∠3=180?,则∠1、∠2、∠3互补
②若∠A=40?26′,则∠A的余角=49?34′
③一个角的补角必为钝角.
②
第二环节
动手实践、探究新知
2
1
O
B
C
A
D
3
4
第二环节
动手实践、探究新知
图1
1.图1中∠1 与∠3 ,∠2与∠3有什么关系;
2.图2.1-10中∠A与∠B ,∠A与∠ACD有什么关系?
答:
1: ∠1 与∠3 互为补交,∠2与∠3互为补交
2: ∠A与∠B互为余角 ,∠A与∠ACD互为余角
3:∠1和∠2有什么关系? ∠B和∠ACD有什么关系?
答:∠1=∠2 ∠B=∠ACD
同角或等角的补角相等
归纳总结
同角或等角的余角相等
问题1:
①.因为∠1+∠2=90?,∠2+∠3=90?,所以∠1= ,理由是
② 因为∠1+∠2=180?,∠2+∠3=180?,所以∠1= ,理由是
巩固练习
第三环节
学以致用,步步为营
∠3
同角或等角的余角相等
同角或等角的补角相等
∠3
问题2:如图2.1—11已知:直线AB与CD交于点O, ∠EOD=900,回答下列问题:
1.∠AOE的余角是 ;补角是. _ __
2.∠AOC的余角是__ ;补角是 ;对顶角是 ___.
巩固练习
C
A
B
D
O
E
2.1─11
第三环节
学以致用,步步为营
∠AOC或∠BOD
∠EOB
∠AOE___
∠AOD_或∠COB__
∠BOD
问题2:①你手中的三角板,如图2-4.则∠A是∠B的 .
变式训练:在①的基础上,做∠CDA=900.
1.则∠A的余角有哪几个?为什么?
2.请找出互补的角,并说明理由.
巩固练习
C
A
B
2.4
C
A
B
2.1─10
D
第四环节
拓展延伸,综合应用
余角
例1、如图,直线a、b相交,∠1=40°,求 ∠2、∠3、∠4的度数。
学以致用:
a
b
)
(
1
3
4
2
)
(
解:由邻补角的定义可知
∠2=180°-∠1
=180°-40°=140°
由对顶角相等可得
∠3=∠1=40°,∠4=∠2=140°
变式:直线AB、CD相交与点O,∠AOC=40°,OE平分∠AOC,求∠DOE的度数。
A
B
O
C
D
E
解:∵OE平分∠AOC, 且∠AOC =40°
∴∠COE= ∠AOC=20°
∵∠DOE与∠COE互为补角
∴∠DOE=180°-∠COE=120°
因此∠DOE=120°
你学到了哪些知识?
第五环节
学有所思,反馈巩固
一、定义:
1、对顶角
2、互为补角,互为余角
二、性质:
对顶角相等
同角或等角的余角相等
同角或等角的补角相等
作业:
课本40页
习题2.1的1;2
第六环节
布置作业,能力延伸
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
