北师大版七年级下册数学课件:2.1两条直线的位置关系(1)(共15张PPT)
文档属性
| 名称 | 北师大版七年级下册数学课件:2.1两条直线的位置关系(1)(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 426.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 15:51:55 | ||
图片预览




文档简介
第二章 相交线与平行线
两条直线的位置关系(1)—
对顶角、补角和余角
对顶角的认识
北师大版初中数学 七年级下册
回顾·思考
在同一平面内,两条直线的位置关系有几种?
分别是哪几种?
在同一平面内,两条直线的位置关系有两种,
分别是相交和平行。
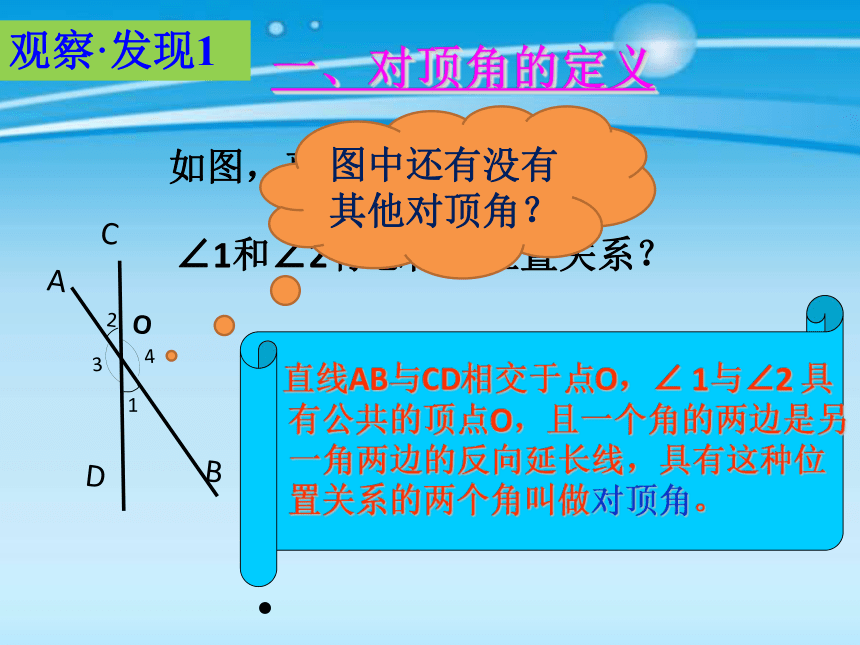
如图,直线AB、CD相交于O
2
1
A
B
C
D
O
3
4
∠1和∠2有怎样的位置关系?
一、对顶角的定义
图中还有没有其他对顶角?
观察·发现1
直线AB与CD相交于点O,∠ 1与∠2 具有公共的顶点O,且一个角的两边是另一角两边的反向延长线,具有这种位置关系的两个角叫做对顶角。
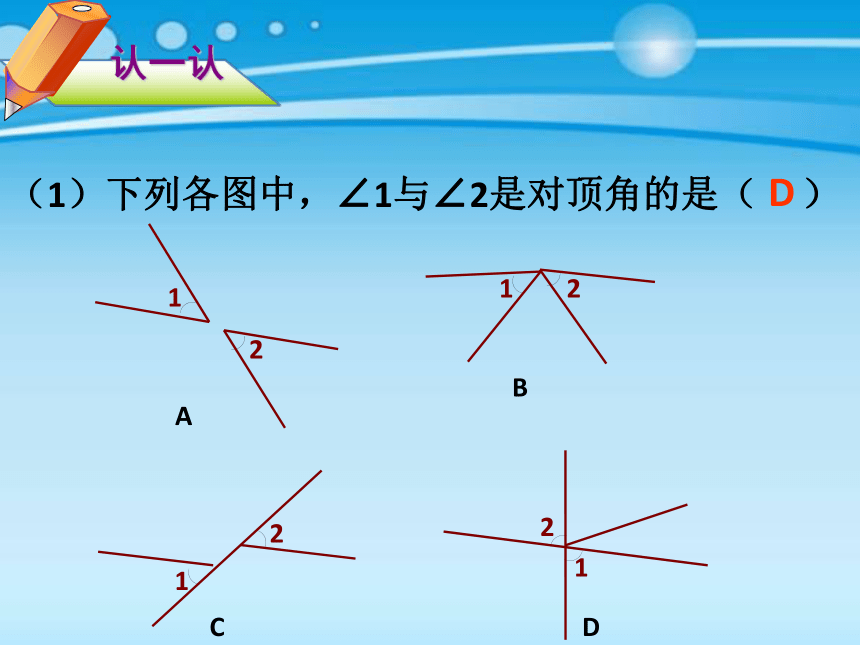
(1)下列各图中,∠1与∠2是对顶角的是( )
1
2
C
1
2
D
D
1
2
A
1
2
B
认一认
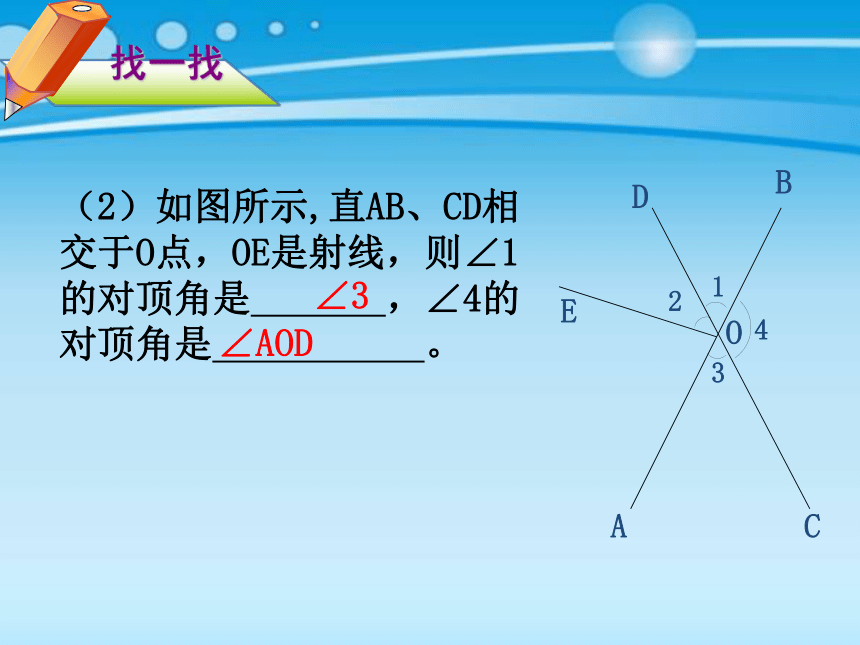
(2)如图所示,直AB、CD相交于O点,OE是射线,则∠1的对顶角是 ,∠4的对顶角是 。
∠AOD
∠3
O
2
1
3
4
E
B
A
C
D
找一找
请你观察图中∠1和∠2这组对顶角,你发现它们的大小有什么关系?再量一量验证一下吧。
观察·发现2
2
1
A
B
C
D
O
对顶角相等
???
已知:如图,直线AB与CD交于O.
求证:∠1=∠2
(二)对顶角的性质:
A
B
D
C
证明:
O
1(
)2
∵∠1 +∠AOC =180° (平角定义)
∠2 +∠AOC =180°(平角定义)
∴∠1 = ∠2 (等式性质)
∴∠1 =180°-∠AOC
∠2 =180°-∠AOC
对顶角相等
!!!
推理·思考
1.如图所示,有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数吗?你能说出所量角是多少度吗?你的根据是什么?
学以致用
方法一:可利用平角定义得出。
︵
︵
1
2
∠1 =180°-∠2
∴ ∠1 = 40°
如图:∵∠2+ ∠1 =180°
所以扇形零件的圆心角的度数是 40°
方法二:可利用对顶角相等得出。
40
0
︵
1
︵
2
如图:∵ ∠1 和∠2是对顶角
∴ ∠1 =∠2
又∵ ∠2=40°
∴ ∠1 =40°
所以扇形零件的圆心角的度数是 40°
学以致用
数学·新课标(BS)
方法一:可利用平角定义得出。
方法二:可利用对顶角相等得出。
总结归纳:
1.对顶角的定义:具有公共的顶点O,且一个角的两边是另一角两边的反向延长线,具有这种位置关系的两个角叫做对顶角。
2.对顶角的性质:对顶角相等。
3.对顶角的性质的应用:解决实际问题。
谢谢观看
两条直线的位置关系(1)—
对顶角、补角和余角
对顶角的认识
北师大版初中数学 七年级下册
回顾·思考
在同一平面内,两条直线的位置关系有几种?
分别是哪几种?
在同一平面内,两条直线的位置关系有两种,
分别是相交和平行。
如图,直线AB、CD相交于O
2
1
A
B
C
D
O
3
4
∠1和∠2有怎样的位置关系?
一、对顶角的定义
图中还有没有其他对顶角?
观察·发现1
直线AB与CD相交于点O,∠ 1与∠2 具有公共的顶点O,且一个角的两边是另一角两边的反向延长线,具有这种位置关系的两个角叫做对顶角。
(1)下列各图中,∠1与∠2是对顶角的是( )
1
2
C
1
2
D
D
1
2
A
1
2
B
认一认
(2)如图所示,直AB、CD相交于O点,OE是射线,则∠1的对顶角是 ,∠4的对顶角是 。
∠AOD
∠3
O
2
1
3
4
E
B
A
C
D
找一找
请你观察图中∠1和∠2这组对顶角,你发现它们的大小有什么关系?再量一量验证一下吧。
观察·发现2
2
1
A
B
C
D
O
对顶角相等
???
已知:如图,直线AB与CD交于O.
求证:∠1=∠2
(二)对顶角的性质:
A
B
D
C
证明:
O
1(
)2
∵∠1 +∠AOC =180° (平角定义)
∠2 +∠AOC =180°(平角定义)
∴∠1 = ∠2 (等式性质)
∴∠1 =180°-∠AOC
∠2 =180°-∠AOC
对顶角相等
!!!
推理·思考
1.如图所示,有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数吗?你能说出所量角是多少度吗?你的根据是什么?
学以致用
方法一:可利用平角定义得出。
︵
︵
1
2
∠1 =180°-∠2
∴ ∠1 = 40°
如图:∵∠2+ ∠1 =180°
所以扇形零件的圆心角的度数是 40°
方法二:可利用对顶角相等得出。
40
0
︵
1
︵
2
如图:∵ ∠1 和∠2是对顶角
∴ ∠1 =∠2
又∵ ∠2=40°
∴ ∠1 =40°
所以扇形零件的圆心角的度数是 40°
学以致用
数学·新课标(BS)
方法一:可利用平角定义得出。
方法二:可利用对顶角相等得出。
总结归纳:
1.对顶角的定义:具有公共的顶点O,且一个角的两边是另一角两边的反向延长线,具有这种位置关系的两个角叫做对顶角。
2.对顶角的性质:对顶角相等。
3.对顶角的性质的应用:解决实际问题。
谢谢观看
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
