人教版数学七年级下册 5.1.2 垂线——课时1 垂线 课件(24张)
文档属性
| 名称 | 人教版数学七年级下册 5.1.2 垂线——课时1 垂线 课件(24张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 781.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 00:00:00 | ||
图片预览



文档简介
第五章 相交线与平行线
5.1 相交线
5.1.2 垂线
课时1 垂线
1.能说出垂线的意义、会用三角尺或量角器过一点画已知直线的垂线.
2.记住垂线的性质并会利用所学知识进行简单的推理. (重点、难点)
学习目标
新课导入
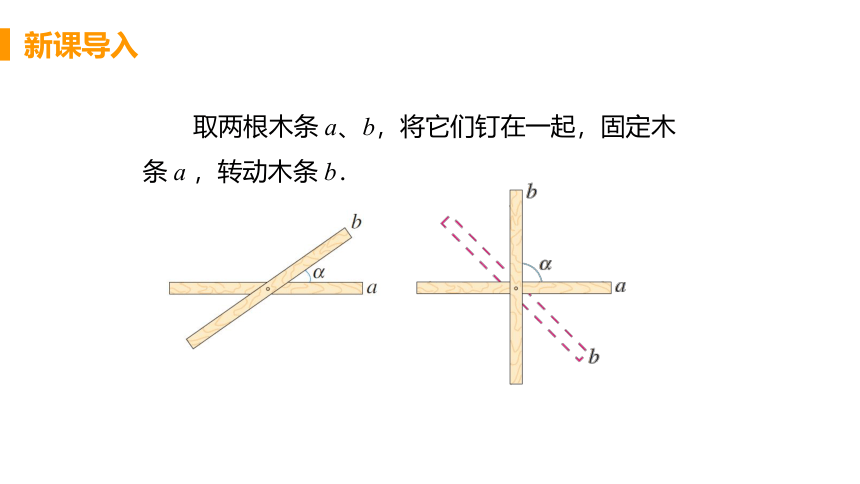
取两根木条 a、b,将它们钉在一起,固定木条 a ,转动木条 b.
新课导入
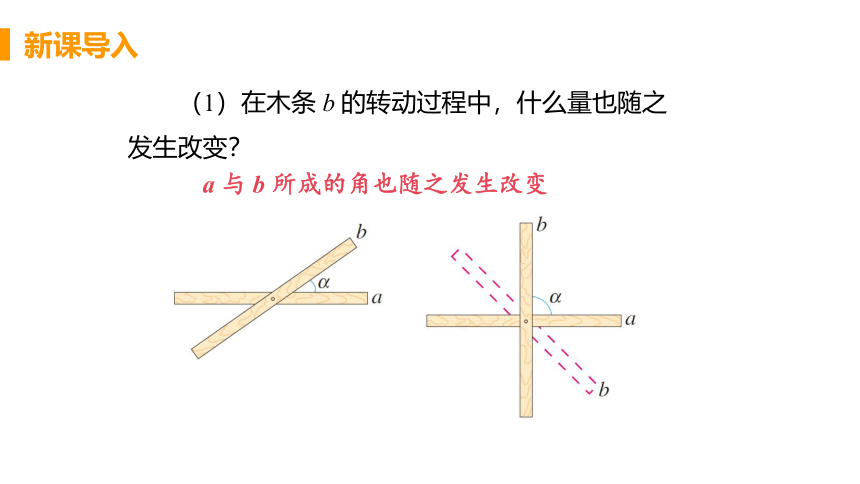
(1)在木条 b 的转动过程中,什么量也随之发生改变?
a 与 b 所成的角也随之发生改变
新课导入
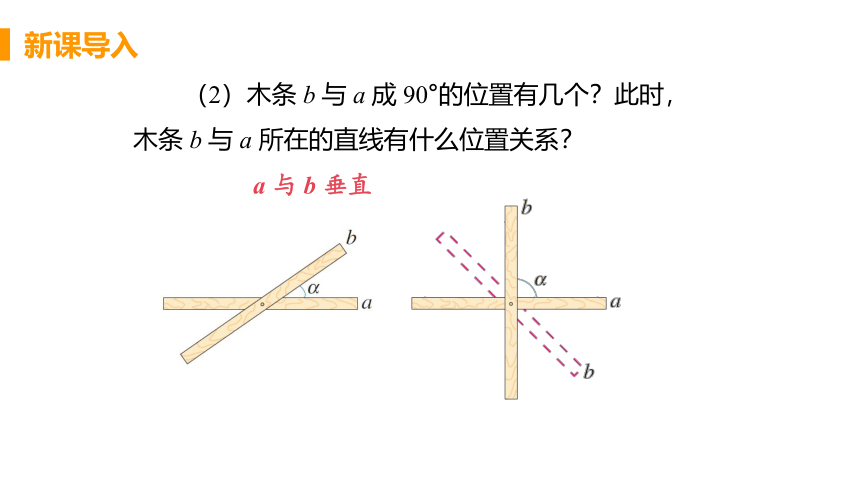
(2)木条 b 与 a 成 90°的位置有几个?此时,木条 b 与 a 所在的直线有什么位置关系?
a 与 b 垂直
新课讲解
知识点1 垂线
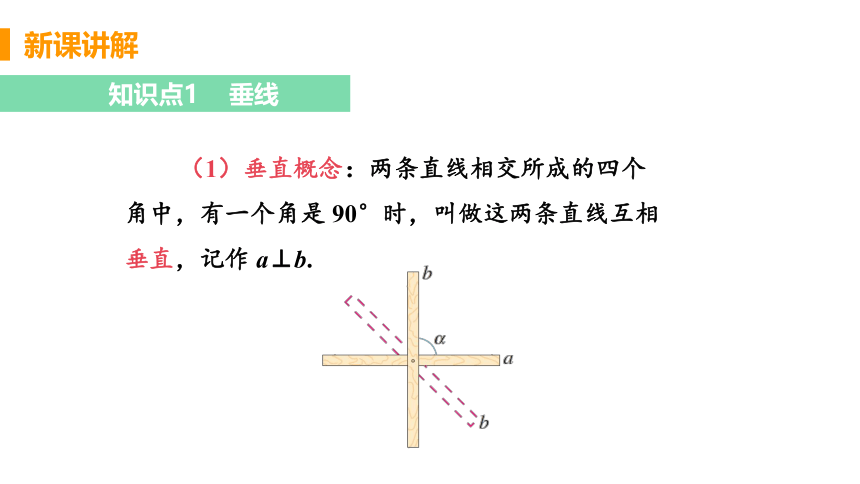
(1)垂直概念:两条直线相交所成的四个角中,有一个角是 90°时,叫做这两条直线互相垂直,记作 a⊥b.
新课讲解
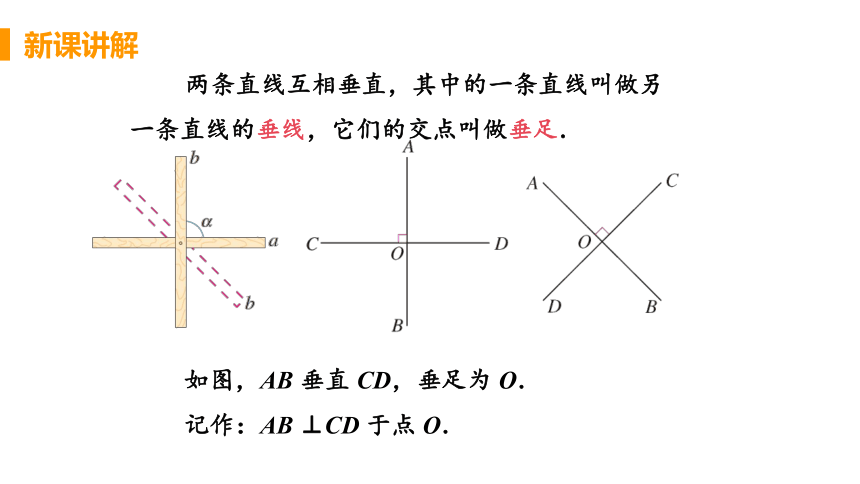
两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
如图,AB 垂直 CD,垂足为 O.
记作:AB ⊥CD 于点 O.
新课讲解
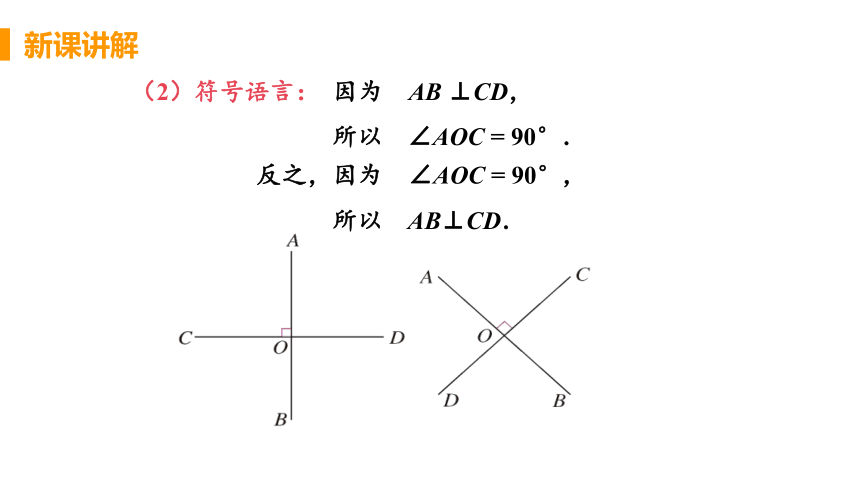
(2)符号语言: 因为 AB ⊥CD,
所以 ∠AOC = 90°.
反之,因为 ∠AOC = 90°,
所以 AB⊥CD.
新课讲解
问题:(1)两条直线垂直和相交是什么关系?
(2)能否认为在同一平面内,两条直线的位置关系有 3 种:相交,平行,垂直?
垂直是相交的特殊情况
不能,因为垂直是相交的特殊情况
新课讲解
(3)如何判定两条射线垂直?两条线段呢?
两条线段垂直、两条射线垂直、线段与射线垂直、线段与直线垂直、射线与直线垂直,都是指它们所在的直线垂直.
新课讲解
例
典例分析
你能举出一些生活中与垂直有关的实例吗?
新课讲解
知识点2 垂线的画法
用三角尺或量角器画已知直线 l 的垂线.
(1)用三角尺或量角器画已知直线 l 的垂线,这样的垂线能画出几条?
无数条
新课讲解
(2)经过一点画已知直线 l 的垂线,这样的垂线能画出几条?
① 经过一点画已知直线 l 的垂线有几种情况?
② 通过画图,你发现过一个点可以画几条直线与已知直线垂直?
2 种
过直线上一点和直线外一点
新课讲解
垂线性质1:在同一平面内,过一点有且只有一条直线与已知直线垂直.
P
l
P
l
新课讲解
例
典例分析
A
B
过点 P 画出射线 AB 或线段 AB 的垂线.
P
A
B
P
(1)
(2)
A
B
P
(3)
新课讲解
例
典例分析
下列说法正确的有( ):①两条直线相交,交点叫做垂足;②在同一平面内,过一点有且只有一条直线与已知直线垂直;③在同一平面内,一条直线有且只有一条垂线;④在同一平面内,一条线段有无数条垂线;⑤过一点不可能向一条射线或线段作垂线;⑥若l1⊥l2,则l1是 l2的垂线,l2不是 l1的垂线. A.2个 B.3个 C.4个 D.5个
A
新课讲解
分析:对垂直的概念和垂线的性质理解不清而判断错误.过一点作线段或射线的垂线,都是指与线段、射线所在的直线垂直.本题中,正确的说法只有②和④.
课堂小结
垂线
定义
画法
当两条直线相交所成的四个角中有一个角为 90°时,这两条直线互相垂直, 其中一条直线叫做另一条直线的垂线
利用三角尺或量角器画:一靠、二过、三画
当堂小练
1. 如图所示,若 AB ⊥ CD 于点 O ,则∠AOD = _____;若∠BOD = 90°,则 AB _____ CD.
90°
⊥
当堂小练
2. 如图,AB ⊥ l ,BC ⊥ l ,B 为垂足,那么 A、B、C 三点在同一直线上吗?为什么?
解:A、B、C 三点在同一直线上.
∵AB ⊥ l ,BC ⊥ l . 且交点都为 B .
∴A、B、C 三点在同一直线上(在同一平面内,
过一点有且只有一条直线与已知直线垂直).
拓展与延伸
如图,直线 AB,CD 相交于 O 点,OM⊥AB 于 O .
(1)若∠1 =∠2,求∠NOD;
(2)若∠BOC = 4∠1,求∠AOC 与∠MOD.
拓展与延伸
解:(1)因为 OM ⊥ AB ,
所以∠1 + ∠AOC = 90°.
又∠1 = ∠2,所以∠2 + ∠AOC = 90°,所
以∠NOD = 180°-(∠2 + ∠AOC)= 180°-
90°= 90°.
拓展与延伸
(2)由已知条件∠BOC =
4∠1,即 90°+∠1 = 4∠1,可
得∠1 = 30°,所以∠AOC = 90°- 30° = 60°,
所以由对顶角相等可得∠BOD = 60°,所以
∠MOD = 90°+∠BOD = 150°.
布置作业
请完成P2-P3对应习题
5.1 相交线
5.1.2 垂线
课时1 垂线
1.能说出垂线的意义、会用三角尺或量角器过一点画已知直线的垂线.
2.记住垂线的性质并会利用所学知识进行简单的推理. (重点、难点)
学习目标
新课导入
取两根木条 a、b,将它们钉在一起,固定木条 a ,转动木条 b.
新课导入
(1)在木条 b 的转动过程中,什么量也随之发生改变?
a 与 b 所成的角也随之发生改变
新课导入
(2)木条 b 与 a 成 90°的位置有几个?此时,木条 b 与 a 所在的直线有什么位置关系?
a 与 b 垂直
新课讲解
知识点1 垂线
(1)垂直概念:两条直线相交所成的四个角中,有一个角是 90°时,叫做这两条直线互相垂直,记作 a⊥b.
新课讲解
两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
如图,AB 垂直 CD,垂足为 O.
记作:AB ⊥CD 于点 O.
新课讲解
(2)符号语言: 因为 AB ⊥CD,
所以 ∠AOC = 90°.
反之,因为 ∠AOC = 90°,
所以 AB⊥CD.
新课讲解
问题:(1)两条直线垂直和相交是什么关系?
(2)能否认为在同一平面内,两条直线的位置关系有 3 种:相交,平行,垂直?
垂直是相交的特殊情况
不能,因为垂直是相交的特殊情况
新课讲解
(3)如何判定两条射线垂直?两条线段呢?
两条线段垂直、两条射线垂直、线段与射线垂直、线段与直线垂直、射线与直线垂直,都是指它们所在的直线垂直.
新课讲解
例
典例分析
你能举出一些生活中与垂直有关的实例吗?
新课讲解
知识点2 垂线的画法
用三角尺或量角器画已知直线 l 的垂线.
(1)用三角尺或量角器画已知直线 l 的垂线,这样的垂线能画出几条?
无数条
新课讲解
(2)经过一点画已知直线 l 的垂线,这样的垂线能画出几条?
① 经过一点画已知直线 l 的垂线有几种情况?
② 通过画图,你发现过一个点可以画几条直线与已知直线垂直?
2 种
过直线上一点和直线外一点
新课讲解
垂线性质1:在同一平面内,过一点有且只有一条直线与已知直线垂直.
P
l
P
l
新课讲解
例
典例分析
A
B
过点 P 画出射线 AB 或线段 AB 的垂线.
P
A
B
P
(1)
(2)
A
B
P
(3)
新课讲解
例
典例分析
下列说法正确的有( ):①两条直线相交,交点叫做垂足;②在同一平面内,过一点有且只有一条直线与已知直线垂直;③在同一平面内,一条直线有且只有一条垂线;④在同一平面内,一条线段有无数条垂线;⑤过一点不可能向一条射线或线段作垂线;⑥若l1⊥l2,则l1是 l2的垂线,l2不是 l1的垂线. A.2个 B.3个 C.4个 D.5个
A
新课讲解
分析:对垂直的概念和垂线的性质理解不清而判断错误.过一点作线段或射线的垂线,都是指与线段、射线所在的直线垂直.本题中,正确的说法只有②和④.
课堂小结
垂线
定义
画法
当两条直线相交所成的四个角中有一个角为 90°时,这两条直线互相垂直, 其中一条直线叫做另一条直线的垂线
利用三角尺或量角器画:一靠、二过、三画
当堂小练
1. 如图所示,若 AB ⊥ CD 于点 O ,则∠AOD = _____;若∠BOD = 90°,则 AB _____ CD.
90°
⊥
当堂小练
2. 如图,AB ⊥ l ,BC ⊥ l ,B 为垂足,那么 A、B、C 三点在同一直线上吗?为什么?
解:A、B、C 三点在同一直线上.
∵AB ⊥ l ,BC ⊥ l . 且交点都为 B .
∴A、B、C 三点在同一直线上(在同一平面内,
过一点有且只有一条直线与已知直线垂直).
拓展与延伸
如图,直线 AB,CD 相交于 O 点,OM⊥AB 于 O .
(1)若∠1 =∠2,求∠NOD;
(2)若∠BOC = 4∠1,求∠AOC 与∠MOD.
拓展与延伸
解:(1)因为 OM ⊥ AB ,
所以∠1 + ∠AOC = 90°.
又∠1 = ∠2,所以∠2 + ∠AOC = 90°,所
以∠NOD = 180°-(∠2 + ∠AOC)= 180°-
90°= 90°.
拓展与延伸
(2)由已知条件∠BOC =
4∠1,即 90°+∠1 = 4∠1,可
得∠1 = 30°,所以∠AOC = 90°- 30° = 60°,
所以由对顶角相等可得∠BOD = 60°,所以
∠MOD = 90°+∠BOD = 150°.
布置作业
请完成P2-P3对应习题
