人教版数学七年级下册 5.1.3 同位角、内错角、同旁内角 课件(26张)
文档属性
| 名称 | 人教版数学七年级下册 5.1.3 同位角、内错角、同旁内角 课件(26张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 463.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 00:00:00 | ||
图片预览


文档简介
第五章 相交线与平行线
5.1 相交线
5.1.3 同位角、内错角、同旁内角
1.能说出同位角、内错角、同旁内角的概念.
2.能结合图形正确找出同位角、内错角、同旁内角.(重点、难点)
学习目标
新课导入
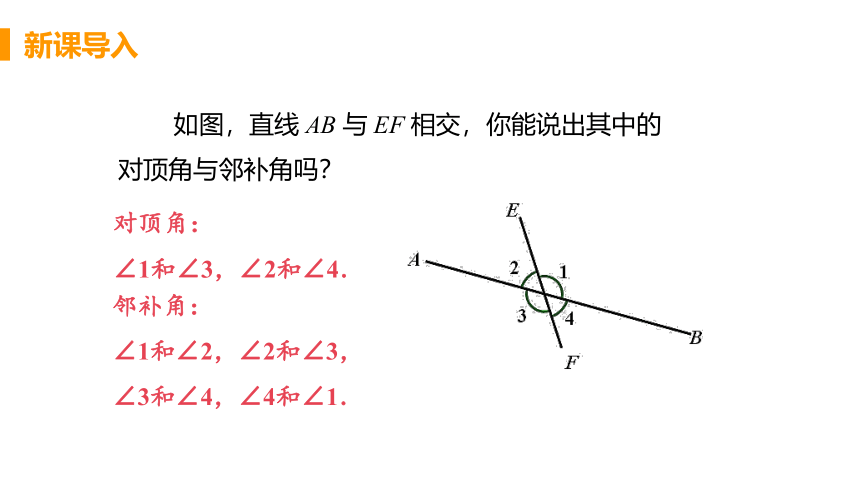
如图,直线 AB 与 EF 相交,你能说出其中的对顶角与邻补角吗?
对顶角:
∠1和∠3,∠2和∠4.
邻补角:
∠1和∠2,∠2和∠3,
∠3和∠4,∠4和∠1.
新课导入
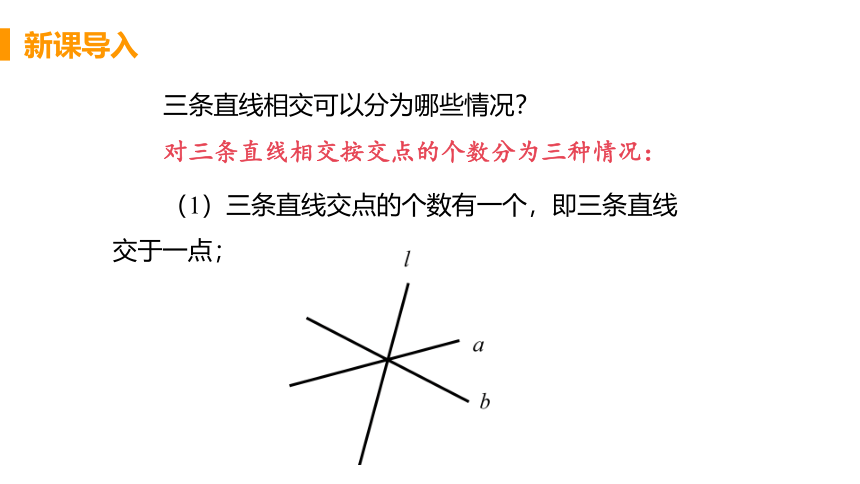
三条直线相交可以分为哪些情况?
对三条直线相交按交点的个数分为三种情况:
(1)三条直线交点的个数有一个,即三条直线交于一点;
新课导入
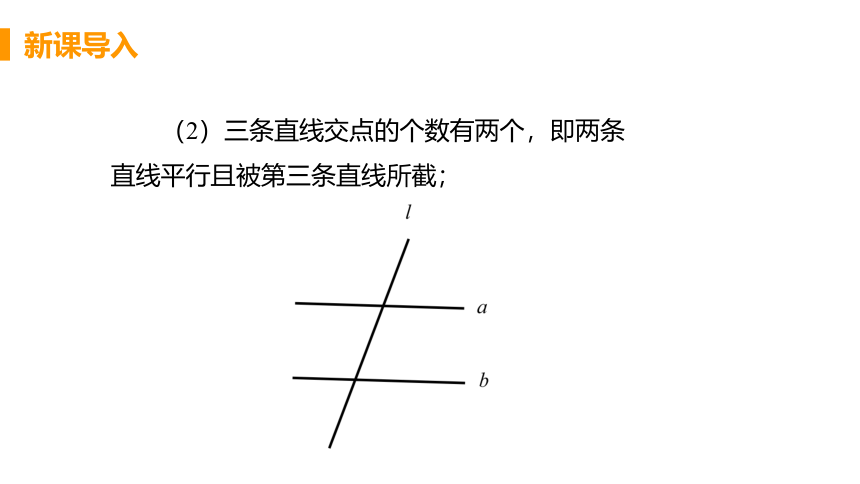
(2)三条直线交点的个数有两个,即两条直线平行且被第三条直线所截;
新课导入
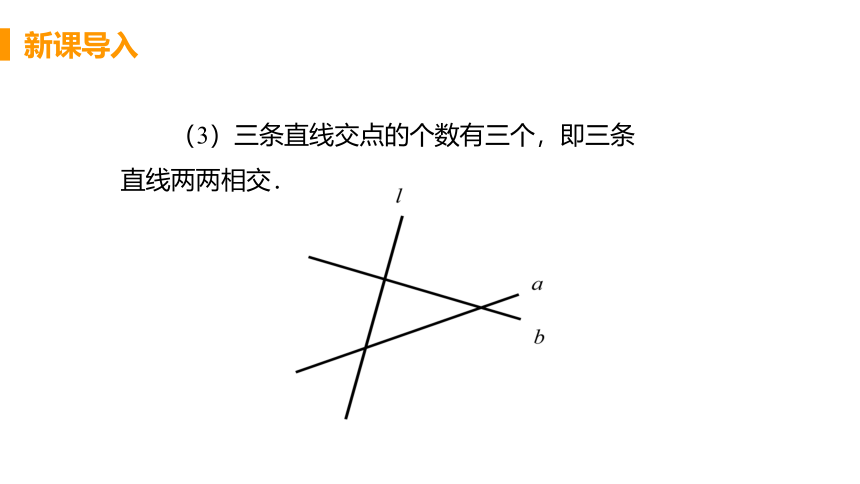
(3)三条直线交点的个数有三个,即三条直线两两相交.
新课讲解
知识点1 同位角
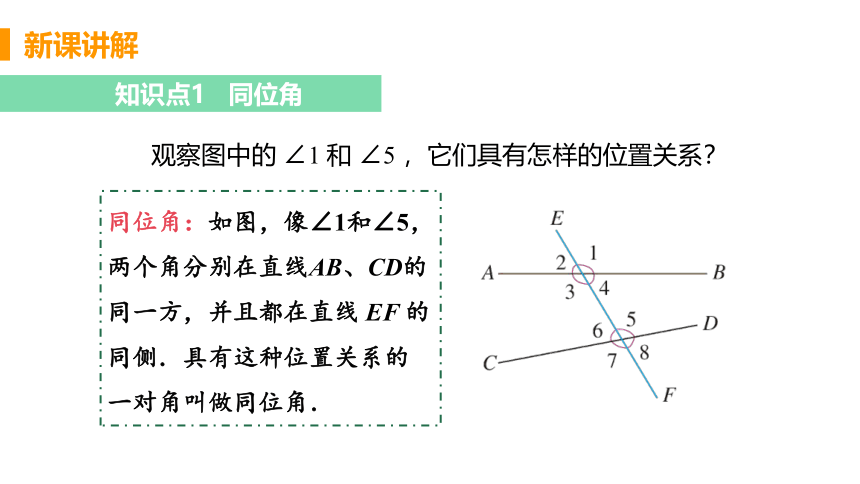
观察图中的 ∠1 和 ∠5 ,它们具有怎样的位置关系?
同位角:如图,像∠1和∠5,两个角分别在直线AB、CD的同一方,并且都在直线 EF 的同侧.具有这种位置关系的一对角叫做同位角.
新课讲解
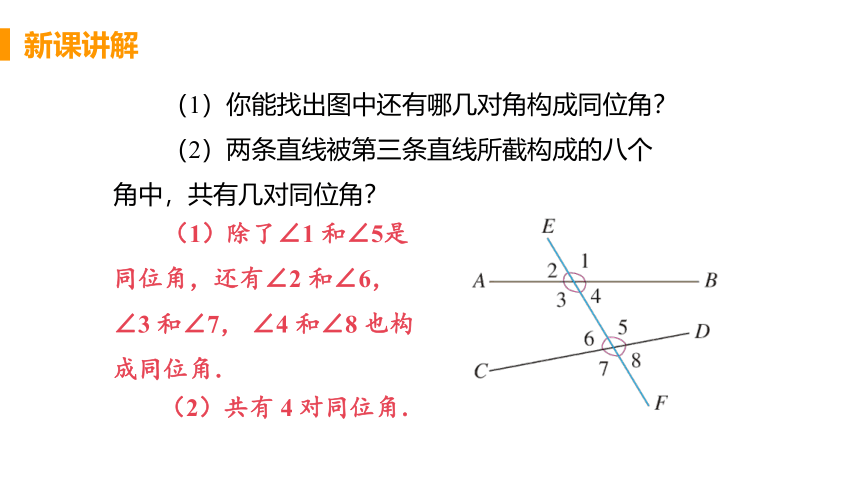
(1)你能找出图中还有哪几对角构成同位角?
(2)两条直线被第三条直线所截构成的八个角中,共有几对同位角?
(1)除了∠1 和∠5是同位角,还有∠2 和∠6,∠3 和∠7, ∠4 和∠8 也构成同位角.
(2)共有 4 对同位角.
新课讲解
知识点2 内错角
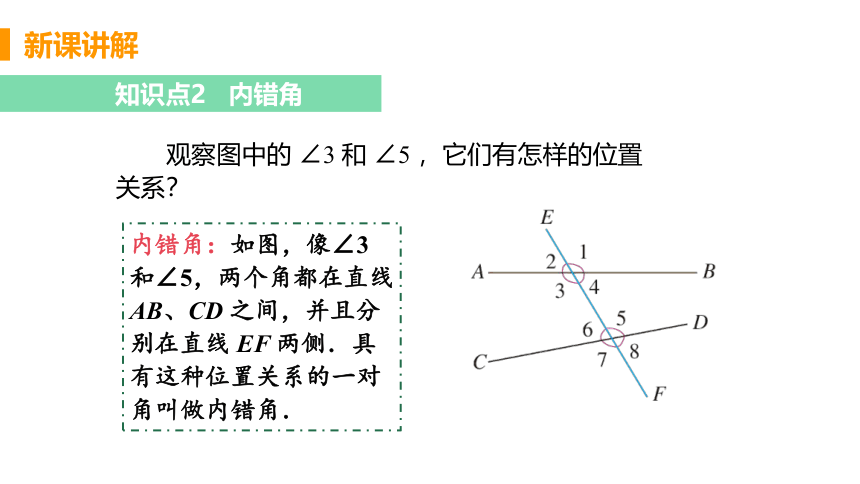
观察图中的 ∠3 和 ∠5 ,它们有怎样的位置关系?
内错角:如图,像∠3 和∠5,两个角都在直线 AB、CD 之间,并且分别在直线 EF 两侧.具有这种位置关系的一对角叫做内错角.
新课讲解
(1)你能找出图中还有哪几对角构成内错角?
(2)两条直线被第三条直线所截构成的八个角中,共有几对内错角?
(1)除了∠3 和∠5是内错角,还有∠4 和∠6 也构成内错角.
(2)共有 2 对内错角.
新课讲解
知识点3 同旁内角
如图,我们称∠3 和∠6 为同旁内角,你能根据两个角的特征,描述一下同旁内角的定义吗?
同旁内角:如图,像∠3和∠6,两个角都在直线AB、CD 之间,并且都在直线 EF 的同一旁.具有这种位置关系的一对角叫做同旁内角.
新课讲解
(1)除了∠3 和∠6是同旁内角,还有∠4 和∠5 也构成同旁内角.
(2)共有 2 对同旁内角.
(1)你能找出图中还有哪几对角构成同旁内角?
(2)两条直线被第三条直线所截构成的八个角中,共有几对同旁内角?
新课讲解
例
典例分析
如图,直线 DE、BC 被直线 AB 所截,
(1)∠1 和∠2,∠1 和∠3,∠1 和∠4 各是什么位置关系的角?
∠1 与 ∠2 是内错角,
∠1 与∠3 是同旁内角,
∠1 与∠4 是同位角.
新课讲解
如果∠1=∠4,由对顶角相等,
得∠2=∠4,那么∠1=∠2.
因为∠4 和∠3 互补,得∠4 + ∠3=180?,
又因为∠1 =∠4,
所以∠1 +∠3 = 180?,
即∠1 和∠3 互补.
如图,直线 DE、BC 被直线 AB 所截,
(2)如果∠1=∠4,那么∠1 和∠2 相等吗?∠1 和∠3 互补吗?为什么?
新课讲解
练一练
1.分别指出下列图中的同位角、内错角、同旁内角.
同位角:∠2 与∠6,∠4 与∠8,∠3 与∠7,∠1 与∠5
内错角:∠3 与∠6,∠4 与∠5
同旁内角:∠3 与∠5,∠4 与∠6
新课讲解
同位角:∠1 与∠3,∠2 与∠4.
内错角:无.
同旁内角:∠2 与 ∠3.
新课讲解
2. 如图,∠B 与哪个角是内错角,与哪个角是同旁内角?它们分别是哪两条直线被哪一条直线所截形成的?对∠C 进行同样的讨论.
新课讲解
解:∠B 与∠DAB 是内错
角,与∠BAE 是同旁内角,它
们都是由 DE 与 BC 被 AB 所截
形成的,还与∠BAC 是同旁内
角,它们是由 AC、BC 被 BA 所截形成的. ∠C 与∠EAC 是内错角,与∠DAC 是同旁内角,它们都是由 DE 与 BC 被 AC 所截形成的. 还与∠BAC 是同旁内角,它们是由 AB、BC 被 AC 所截形成的.
课堂小结
1.你能总结一下同位角、内错角、同旁内角分别具有哪些特征吗?
2.你认为在图形中识别同位角、内错角、同旁内角的关键是什么?
当堂小练
如图,∠1 和∠2,∠3 和∠4 是由哪两条直线被一条直线所截形成的?它们各是什么位置关系的角?
(1) (2)
当堂小练
(1)
解:(1)∠1 和 ∠2 是由直线 DC、AB 被 BD 所截形成的内错角,
∠3 和∠4 是由直线 AD、BC 被 BD 所截形成的内错角.
当堂小练
(2)∠1 和 ∠2 是由直线 AB、CD 被 BC 所截形成的同旁内角.
∠3 和 ∠4 是由直线 AD、BC 被 AE 所截形成的同位角.
(2)
拓展与延伸
直线 AB,CD 相交于点 O .
(1)OE、OF 分别是∠AOC、∠BOD 的平分线,画出这个图形;
(2)射线 OE、OF 在同一条直线上吗?
(3)画出∠AOD 的平分线 OG,OE 与 OG 有怎样的位置关系?为什么?
拓展与延伸
解:(1)如图:
(2)射线 OE、OF 在同一条直线上.
拓展与延伸
OE⊥OG .
因为OE平分∠AOC,所以∠AOE = ∠AOC.
同理:∠AOG = ∠AOD .
所以∠AOE + ∠AOG = (∠AOC +∠AOD)= ×180°= 90°.
所以OE⊥OG .
(3)
G
布置作业
请完成 P2-P3对应习题
5.1 相交线
5.1.3 同位角、内错角、同旁内角
1.能说出同位角、内错角、同旁内角的概念.
2.能结合图形正确找出同位角、内错角、同旁内角.(重点、难点)
学习目标
新课导入
如图,直线 AB 与 EF 相交,你能说出其中的对顶角与邻补角吗?
对顶角:
∠1和∠3,∠2和∠4.
邻补角:
∠1和∠2,∠2和∠3,
∠3和∠4,∠4和∠1.
新课导入
三条直线相交可以分为哪些情况?
对三条直线相交按交点的个数分为三种情况:
(1)三条直线交点的个数有一个,即三条直线交于一点;
新课导入
(2)三条直线交点的个数有两个,即两条直线平行且被第三条直线所截;
新课导入
(3)三条直线交点的个数有三个,即三条直线两两相交.
新课讲解
知识点1 同位角
观察图中的 ∠1 和 ∠5 ,它们具有怎样的位置关系?
同位角:如图,像∠1和∠5,两个角分别在直线AB、CD的同一方,并且都在直线 EF 的同侧.具有这种位置关系的一对角叫做同位角.
新课讲解
(1)你能找出图中还有哪几对角构成同位角?
(2)两条直线被第三条直线所截构成的八个角中,共有几对同位角?
(1)除了∠1 和∠5是同位角,还有∠2 和∠6,∠3 和∠7, ∠4 和∠8 也构成同位角.
(2)共有 4 对同位角.
新课讲解
知识点2 内错角
观察图中的 ∠3 和 ∠5 ,它们有怎样的位置关系?
内错角:如图,像∠3 和∠5,两个角都在直线 AB、CD 之间,并且分别在直线 EF 两侧.具有这种位置关系的一对角叫做内错角.
新课讲解
(1)你能找出图中还有哪几对角构成内错角?
(2)两条直线被第三条直线所截构成的八个角中,共有几对内错角?
(1)除了∠3 和∠5是内错角,还有∠4 和∠6 也构成内错角.
(2)共有 2 对内错角.
新课讲解
知识点3 同旁内角
如图,我们称∠3 和∠6 为同旁内角,你能根据两个角的特征,描述一下同旁内角的定义吗?
同旁内角:如图,像∠3和∠6,两个角都在直线AB、CD 之间,并且都在直线 EF 的同一旁.具有这种位置关系的一对角叫做同旁内角.
新课讲解
(1)除了∠3 和∠6是同旁内角,还有∠4 和∠5 也构成同旁内角.
(2)共有 2 对同旁内角.
(1)你能找出图中还有哪几对角构成同旁内角?
(2)两条直线被第三条直线所截构成的八个角中,共有几对同旁内角?
新课讲解
例
典例分析
如图,直线 DE、BC 被直线 AB 所截,
(1)∠1 和∠2,∠1 和∠3,∠1 和∠4 各是什么位置关系的角?
∠1 与 ∠2 是内错角,
∠1 与∠3 是同旁内角,
∠1 与∠4 是同位角.
新课讲解
如果∠1=∠4,由对顶角相等,
得∠2=∠4,那么∠1=∠2.
因为∠4 和∠3 互补,得∠4 + ∠3=180?,
又因为∠1 =∠4,
所以∠1 +∠3 = 180?,
即∠1 和∠3 互补.
如图,直线 DE、BC 被直线 AB 所截,
(2)如果∠1=∠4,那么∠1 和∠2 相等吗?∠1 和∠3 互补吗?为什么?
新课讲解
练一练
1.分别指出下列图中的同位角、内错角、同旁内角.
同位角:∠2 与∠6,∠4 与∠8,∠3 与∠7,∠1 与∠5
内错角:∠3 与∠6,∠4 与∠5
同旁内角:∠3 与∠5,∠4 与∠6
新课讲解
同位角:∠1 与∠3,∠2 与∠4.
内错角:无.
同旁内角:∠2 与 ∠3.
新课讲解
2. 如图,∠B 与哪个角是内错角,与哪个角是同旁内角?它们分别是哪两条直线被哪一条直线所截形成的?对∠C 进行同样的讨论.
新课讲解
解:∠B 与∠DAB 是内错
角,与∠BAE 是同旁内角,它
们都是由 DE 与 BC 被 AB 所截
形成的,还与∠BAC 是同旁内
角,它们是由 AC、BC 被 BA 所截形成的. ∠C 与∠EAC 是内错角,与∠DAC 是同旁内角,它们都是由 DE 与 BC 被 AC 所截形成的. 还与∠BAC 是同旁内角,它们是由 AB、BC 被 AC 所截形成的.
课堂小结
1.你能总结一下同位角、内错角、同旁内角分别具有哪些特征吗?
2.你认为在图形中识别同位角、内错角、同旁内角的关键是什么?
当堂小练
如图,∠1 和∠2,∠3 和∠4 是由哪两条直线被一条直线所截形成的?它们各是什么位置关系的角?
(1) (2)
当堂小练
(1)
解:(1)∠1 和 ∠2 是由直线 DC、AB 被 BD 所截形成的内错角,
∠3 和∠4 是由直线 AD、BC 被 BD 所截形成的内错角.
当堂小练
(2)∠1 和 ∠2 是由直线 AB、CD 被 BC 所截形成的同旁内角.
∠3 和 ∠4 是由直线 AD、BC 被 AE 所截形成的同位角.
(2)
拓展与延伸
直线 AB,CD 相交于点 O .
(1)OE、OF 分别是∠AOC、∠BOD 的平分线,画出这个图形;
(2)射线 OE、OF 在同一条直线上吗?
(3)画出∠AOD 的平分线 OG,OE 与 OG 有怎样的位置关系?为什么?
拓展与延伸
解:(1)如图:
(2)射线 OE、OF 在同一条直线上.
拓展与延伸
OE⊥OG .
因为OE平分∠AOC,所以∠AOE = ∠AOC.
同理:∠AOG = ∠AOD .
所以∠AOE + ∠AOG = (∠AOC +∠AOD)= ×180°= 90°.
所以OE⊥OG .
(3)
G
布置作业
请完成 P2-P3对应习题
