人教版数学七年级下册 5.2.2 平行线的判定 课件(22张)
文档属性
| 名称 | 人教版数学七年级下册 5.2.2 平行线的判定 课件(22张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 804.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 15:31:15 | ||
图片预览






文档简介
第五章
相交线与平行线
5.2
平行线及其判定
5.2.2
平行线的判定
1.学会并记住平行线的判定方法
1、2、3.
2.能运用平行线的判定方法进行简单的推理论证.(重点、难点)
学习目标
新课导入
上节课我们学行线的概念和画法,这节课我们来研究如何判定两条直线是不是平行线.
新课讲解
知识点1
平行线的判定方法
1、2、3
如何判断两条直线是否平行?
(1)
根据定义.
(2)
根据平行公理的推论.
新课讲解
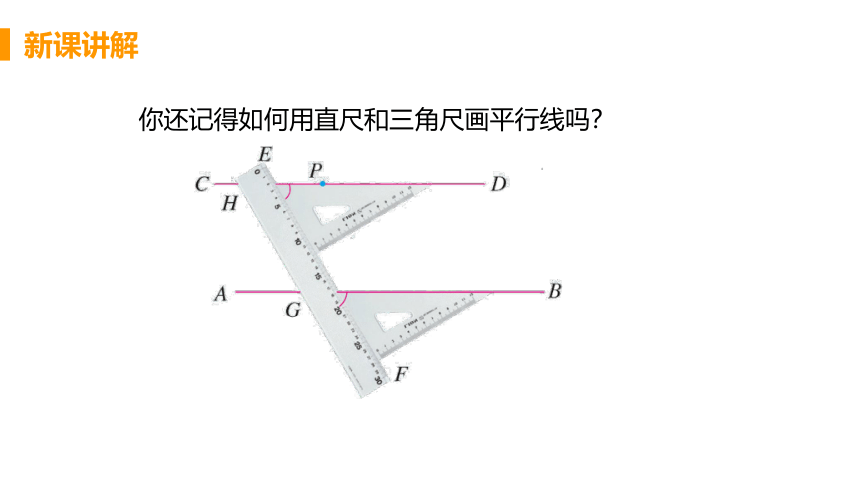
你还记得如何用直尺和三角尺画平行线吗?
新课讲解
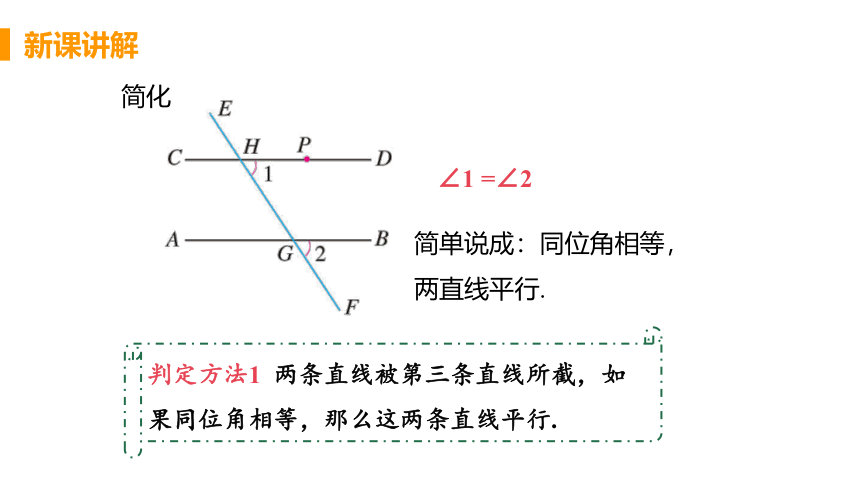
判定方法1
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
∠1
=∠2
简化
新课讲解
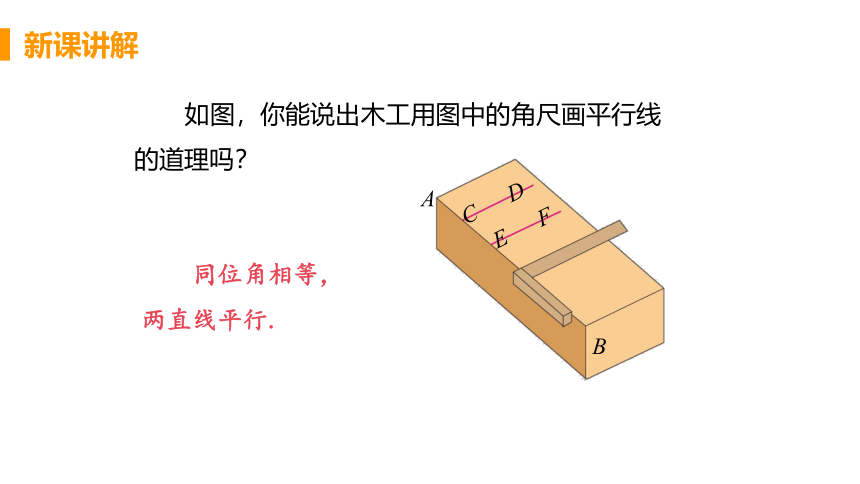
同位角相等,两直线平行.
如图,你能说出木工用图中的角尺画平行线的道理吗?
A
B
C
D
E
F
新课讲解
如果两条直线被第三条直线所截,那么能否利用内错角来判定两条直线平行呢?
如图,如果∠2
=∠3,那么
a
与
b
平行吗?
因为∠2
=∠3,∠3
=∠1,
所以∠1
=∠2,
所以
a∥b
.
新课讲解
判定方法2
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
新课讲解
如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢?
如图,如果∠2
+∠4
=
180°,那么
a
与
b
平行吗?
因为∠2
+∠4
=
180°,
∠1
+∠4
=
180°,
所以∠1
=
∠2,
所以
a∥b
.
新课讲解
判定方法3
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
新课讲解
判定方法
1
同位角相等,两直线平行.
判定方法
2
内错角相等,两直线平行.
判定方法
3
同旁内角互补,两直线平行.
平行线的判定
新课讲解
知识点2
同一平面内,同垂直于第三条直线的两直线平行
例
在同一平面内,如果两条直线都垂直于同一条直线,那么两条直线平行吗?为什么?
已知条件:直线
b
与直线
c
都垂直于直线
a
.
要说明的结论:直线
b
与直线
c
平行吗?
新课讲解
答:直线
b
与直线
c
平行.
理由如下:
∵
b⊥a,∴
∠1=
90°.
同理∠2=
90°.
∴
∠1=∠2.
∵
∠1
和∠2
是同位角,
∴
b∥c(同位角相等,两直线平行).
你还能用其他方法说明理由吗?
新课讲解
练一练
1.
如图,
BE
是
AB
的延长线.
(1)由∠CBE
=∠A
可以判定哪两条直线平行?根据是什么?
答:
AD∥BC
.
根据同位角相等,两直线平行.
新课讲解
(2)由∠CBE
=∠C
可以判定哪两条直线平行?根据是什么?
答:
AE∥CD
.
根据内错角相等,两直线平行.
新课讲解
答:
AE∥CD
.
根据同旁内角互补,两直线平行.
(3)由∠D
+∠A
=
180°可以判定哪两条直线平行?根据是什么?
课堂小结
平行线的判定
①平行公理的推论:如果两条直线都与第三条直线平行,这两条直线也互相平行.
②判定方法
1:同位角相等,两直线平行.
③判定方法
2:内错角相等,两直线平行.
④判定方法
3:同旁内角互补,两直线平行.
⑤同一平面内,垂直于同一直线的两条直线平行.
应用:判定生活中的平行线
当堂小练
1.
如图,为了加固房屋,要在屋架上加一根横梁
DE,使
DE∥BC.
如果∠ABC
=
31°,∠ADE
应为多少度?
A
D
E
B
O
C
解:要使
DE∥BC,需∠ADE
=
∠ABC,而∠ABC
=
31°,∴∠ADE
=
31°.
根据“同位角相等,两直线平行”.
当堂小练
2.
如图,有一块方形玻璃,用什么方法可以检验它相对的两条边是否平行?
解:如图,可测∠1
与∠2,若∠1+∠2
=
180°,则可判断上下两边平行;然后再测∠2
与∠3,若∠2+∠3
=
180°,则可判断左右两边平行.
拓展与延伸
如图所示,已知直线
a,b,c,d,e,且∠1
=
∠2,∠3
+
∠4
=
180°,则
a
与
c
平行吗?为什么?
解:∵∠1
=
∠2,
∴
a∥b(内错角相等,两直线平行).
∵∠3
+
∠4
=
180°,
∴b∥c(同旁内角互补,两直线平行).
又∵
a∥b,
∴
a∥c(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
布置作业
请完成P2-P3对应习题
相交线与平行线
5.2
平行线及其判定
5.2.2
平行线的判定
1.学会并记住平行线的判定方法
1、2、3.
2.能运用平行线的判定方法进行简单的推理论证.(重点、难点)
学习目标
新课导入
上节课我们学行线的概念和画法,这节课我们来研究如何判定两条直线是不是平行线.
新课讲解
知识点1
平行线的判定方法
1、2、3
如何判断两条直线是否平行?
(1)
根据定义.
(2)
根据平行公理的推论.
新课讲解
你还记得如何用直尺和三角尺画平行线吗?
新课讲解
判定方法1
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
∠1
=∠2
简化
新课讲解
同位角相等,两直线平行.
如图,你能说出木工用图中的角尺画平行线的道理吗?
A
B
C
D
E
F
新课讲解
如果两条直线被第三条直线所截,那么能否利用内错角来判定两条直线平行呢?
如图,如果∠2
=∠3,那么
a
与
b
平行吗?
因为∠2
=∠3,∠3
=∠1,
所以∠1
=∠2,
所以
a∥b
.
新课讲解
判定方法2
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
新课讲解
如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢?
如图,如果∠2
+∠4
=
180°,那么
a
与
b
平行吗?
因为∠2
+∠4
=
180°,
∠1
+∠4
=
180°,
所以∠1
=
∠2,
所以
a∥b
.
新课讲解
判定方法3
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
新课讲解
判定方法
1
同位角相等,两直线平行.
判定方法
2
内错角相等,两直线平行.
判定方法
3
同旁内角互补,两直线平行.
平行线的判定
新课讲解
知识点2
同一平面内,同垂直于第三条直线的两直线平行
例
在同一平面内,如果两条直线都垂直于同一条直线,那么两条直线平行吗?为什么?
已知条件:直线
b
与直线
c
都垂直于直线
a
.
要说明的结论:直线
b
与直线
c
平行吗?
新课讲解
答:直线
b
与直线
c
平行.
理由如下:
∵
b⊥a,∴
∠1=
90°.
同理∠2=
90°.
∴
∠1=∠2.
∵
∠1
和∠2
是同位角,
∴
b∥c(同位角相等,两直线平行).
你还能用其他方法说明理由吗?
新课讲解
练一练
1.
如图,
BE
是
AB
的延长线.
(1)由∠CBE
=∠A
可以判定哪两条直线平行?根据是什么?
答:
AD∥BC
.
根据同位角相等,两直线平行.
新课讲解
(2)由∠CBE
=∠C
可以判定哪两条直线平行?根据是什么?
答:
AE∥CD
.
根据内错角相等,两直线平行.
新课讲解
答:
AE∥CD
.
根据同旁内角互补,两直线平行.
(3)由∠D
+∠A
=
180°可以判定哪两条直线平行?根据是什么?
课堂小结
平行线的判定
①平行公理的推论:如果两条直线都与第三条直线平行,这两条直线也互相平行.
②判定方法
1:同位角相等,两直线平行.
③判定方法
2:内错角相等,两直线平行.
④判定方法
3:同旁内角互补,两直线平行.
⑤同一平面内,垂直于同一直线的两条直线平行.
应用:判定生活中的平行线
当堂小练
1.
如图,为了加固房屋,要在屋架上加一根横梁
DE,使
DE∥BC.
如果∠ABC
=
31°,∠ADE
应为多少度?
A
D
E
B
O
C
解:要使
DE∥BC,需∠ADE
=
∠ABC,而∠ABC
=
31°,∴∠ADE
=
31°.
根据“同位角相等,两直线平行”.
当堂小练
2.
如图,有一块方形玻璃,用什么方法可以检验它相对的两条边是否平行?
解:如图,可测∠1
与∠2,若∠1+∠2
=
180°,则可判断上下两边平行;然后再测∠2
与∠3,若∠2+∠3
=
180°,则可判断左右两边平行.
拓展与延伸
如图所示,已知直线
a,b,c,d,e,且∠1
=
∠2,∠3
+
∠4
=
180°,则
a
与
c
平行吗?为什么?
解:∵∠1
=
∠2,
∴
a∥b(内错角相等,两直线平行).
∵∠3
+
∠4
=
180°,
∴b∥c(同旁内角互补,两直线平行).
又∵
a∥b,
∴
a∥c(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
布置作业
请完成P2-P3对应习题
