鲁教版(五四制)九年级数学下册第五章 5.8 正多边形和圆 同步练习(word版无答案)
文档属性
| 名称 | 鲁教版(五四制)九年级数学下册第五章 5.8 正多边形和圆 同步练习(word版无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 88.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 00:00:00 | ||
图片预览

文档简介
5.8正多边形和圆
同步练习
半径为R的圆内接正三角形、正方形、正六边形的边心距分别为a,b,c,则a,b,c的大小关系是
A.
B.
C.
D.
边长为2的正六边形的边心距是
A.
2
B.
1
C.
D.
若正n边形的一个内角为135°,那么n的值为( )
A.
12
B.
10
C.
8
D.
7
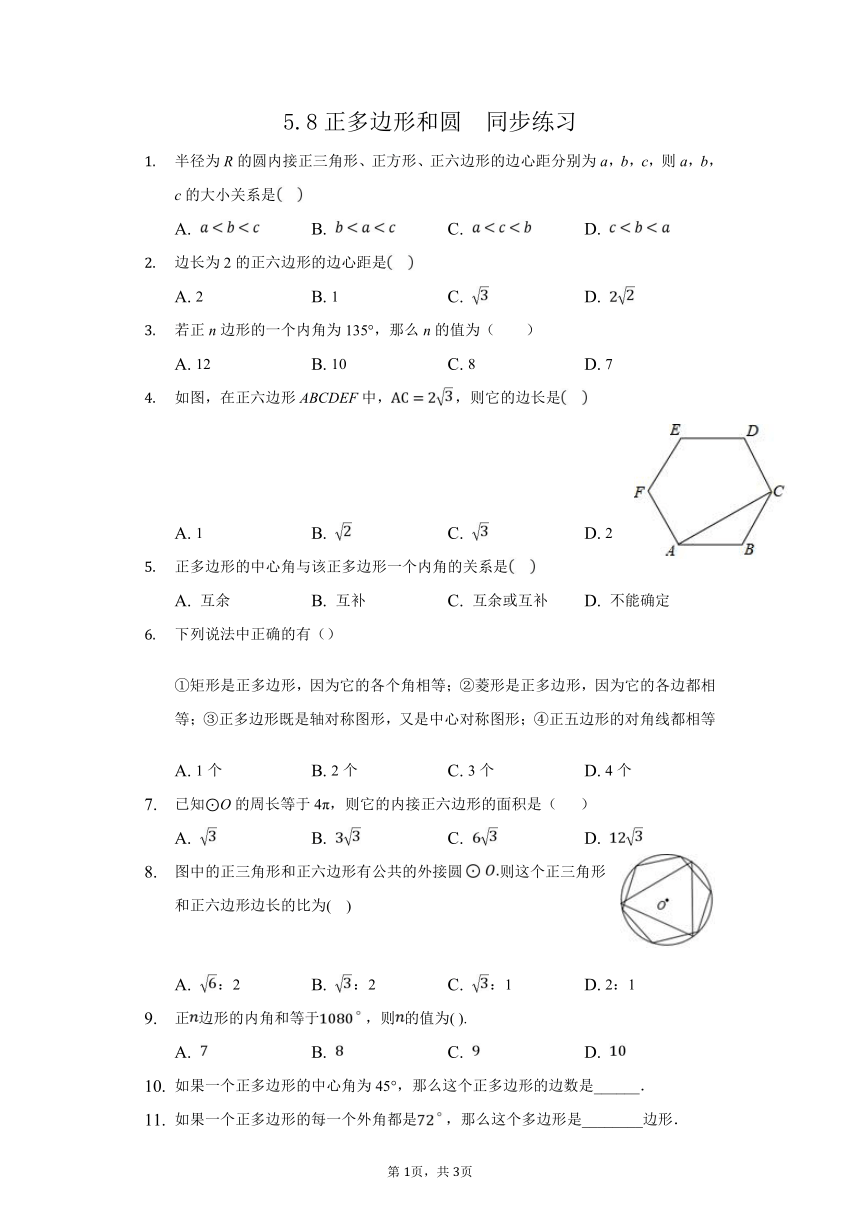
如图,在正六边形ABCDEF中,,则它的边长是
A.
1
B.
C.
D.
2
正多边形的中心角与该正多边形一个内角的关系是
A.
互余
B.
互补
C.
互余或互补
D.
不能确定
下列说法中正确的有()
①矩形是正多边形,因为它的各个角相等;②菱形是正多边形,因为它的各边都相等;③正多边形既是轴对称图形,又是中心对称图形;④正五边形的对角线都相等
A.
1个
B.
2个
C.
3个
D.
4个
已知⊙O的周长等于4π,则它的内接正六边形的面积是(????
)
A.
B.
C.
D.
图中的正三角形和正六边形有公共的外接圆则这个正三角形和正六边形边长的比为(????)
A.
:2
B.
:2
C.
:1
D.
2:1
正边形的内角和等于,则的值为(
).
A.
B.
C.
D.
如果一个正多边形的中心角为45°,那么这个正多边形的边数是______.
如果一个正多边形的每一个外角都是,那么这个多边形是________边形.
如图,在平面直角坐标系中,正六边形OABCDE边长是6,则它的外接圆心P的坐标是________.
某正多边形的边心距为,半径为4,则该正多边形的面积为______.
如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)求证:△ABC是等边三角形.
(2)若⊙O的半径为2,求等边△ABC的边心距.
如图所示,把O分成三等分,经过各点作圆的切线,以相邻的切线交点为顶点的三角形是这个圆的外切正三角形,若正三角形ABC的外接圆半径为2,则外切正三角形的边长有多长?
如图,已知:边长为1的圆内接正方形ABCD中,P为边CD的中点,直线AP交圆于E点.
(1)求弦DE的长.
(2)若Q是线段BC上一动点,当BQ长为何值时,△ADP与以Q,C,P为顶点的三角形相似?
如图,分别求出半径为R的圆内接正三角形圆内接正方形的周长和面积.
第2页,共2页
第1页,共1页
同步练习
半径为R的圆内接正三角形、正方形、正六边形的边心距分别为a,b,c,则a,b,c的大小关系是
A.
B.
C.
D.
边长为2的正六边形的边心距是
A.
2
B.
1
C.
D.
若正n边形的一个内角为135°,那么n的值为( )
A.
12
B.
10
C.
8
D.
7
如图,在正六边形ABCDEF中,,则它的边长是
A.
1
B.
C.
D.
2
正多边形的中心角与该正多边形一个内角的关系是
A.
互余
B.
互补
C.
互余或互补
D.
不能确定
下列说法中正确的有()
①矩形是正多边形,因为它的各个角相等;②菱形是正多边形,因为它的各边都相等;③正多边形既是轴对称图形,又是中心对称图形;④正五边形的对角线都相等
A.
1个
B.
2个
C.
3个
D.
4个
已知⊙O的周长等于4π,则它的内接正六边形的面积是(????
)
A.
B.
C.
D.
图中的正三角形和正六边形有公共的外接圆则这个正三角形和正六边形边长的比为(????)
A.
:2
B.
:2
C.
:1
D.
2:1
正边形的内角和等于,则的值为(
).
A.
B.
C.
D.
如果一个正多边形的中心角为45°,那么这个正多边形的边数是______.
如果一个正多边形的每一个外角都是,那么这个多边形是________边形.
如图,在平面直角坐标系中,正六边形OABCDE边长是6,则它的外接圆心P的坐标是________.
某正多边形的边心距为,半径为4,则该正多边形的面积为______.
如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)求证:△ABC是等边三角形.
(2)若⊙O的半径为2,求等边△ABC的边心距.
如图所示,把O分成三等分,经过各点作圆的切线,以相邻的切线交点为顶点的三角形是这个圆的外切正三角形,若正三角形ABC的外接圆半径为2,则外切正三角形的边长有多长?
如图,已知:边长为1的圆内接正方形ABCD中,P为边CD的中点,直线AP交圆于E点.
(1)求弦DE的长.
(2)若Q是线段BC上一动点,当BQ长为何值时,△ADP与以Q,C,P为顶点的三角形相似?
如图,分别求出半径为R的圆内接正三角形圆内接正方形的周长和面积.
第2页,共2页
第1页,共1页
