沪教版(上海)数学八年级第二学期-21.7 (1)列方程(组)解应用题 教案
文档属性
| 名称 | 沪教版(上海)数学八年级第二学期-21.7 (1)列方程(组)解应用题 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 131.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 00:00:00 | ||
图片预览


文档简介
21.7
(1)列方程(组)解应用题
教学目标:通过复习百分率的应用引出一元高次方程的应用题,体验列方程解应用题的一般方法与步骤;经历对“问题三”容器的选择的讨论,理解方程的根在实际问题中检验的重要性;经历“实际问题-建立方程-方程求解-解释应用”的过程,体会方程思想,感知数学模型思想;依托垃圾分类为背景,体会方程的应用价值,增强数学应用意识,透过数据强化垃圾分类的重要性.
教学重点:体验列整式方程解决简单实际问题的过程.
教学难点:会列方程(组)解决简单的实际问题.
教学过程
设计意图
情境引入
问题一:你知道你每天会生产多少垃圾吗?
1.随着我们的生活越来越便利、物品越来越丰富我们丢弃的生活垃圾也就变得越来越多.上海2017年平均每人每天产生近1千克垃圾,并以每年20%的平均速度在增长,那么到了2018年,上海平均每人每天生产近
千克生活垃圾.
由旧知增长率问题引入本节课,抛出以垃圾分类为故事背景的这个“锚”,开始整堂课的研究.
二、新知学习
2.上海市在2000年就成为国内首批生活垃圾分类收集试点城市,开展了许多垃圾分类的探索性工作。根据最新的《上海市生活垃圾全程分类体系建设行动》,上海市生活垃圾综合处理能力从2018年底的2.5万吨/日,提高到2020年底的3.025万吨/日,若每年的平均增长率相同,求这个平均增长率.
要求:
学生独立思考;
学生板眼交流;
师生共同归纳解应用题的一般步骤.
揭示课题:21.7(1)列方程解应用题
练习:“再生能源中心”为实现零填埋,在2018年干垃圾末端处置达到2.14万吨/日,如果2019年的下降率为m,2020年的下降率比2019年又降低3%,且干垃圾末端处置为1.81万吨/日,根据题意,可列出方程为(
)
(B)
(C)
(D)
问题二:人类产生的垃圾的寿命究竟有多长?
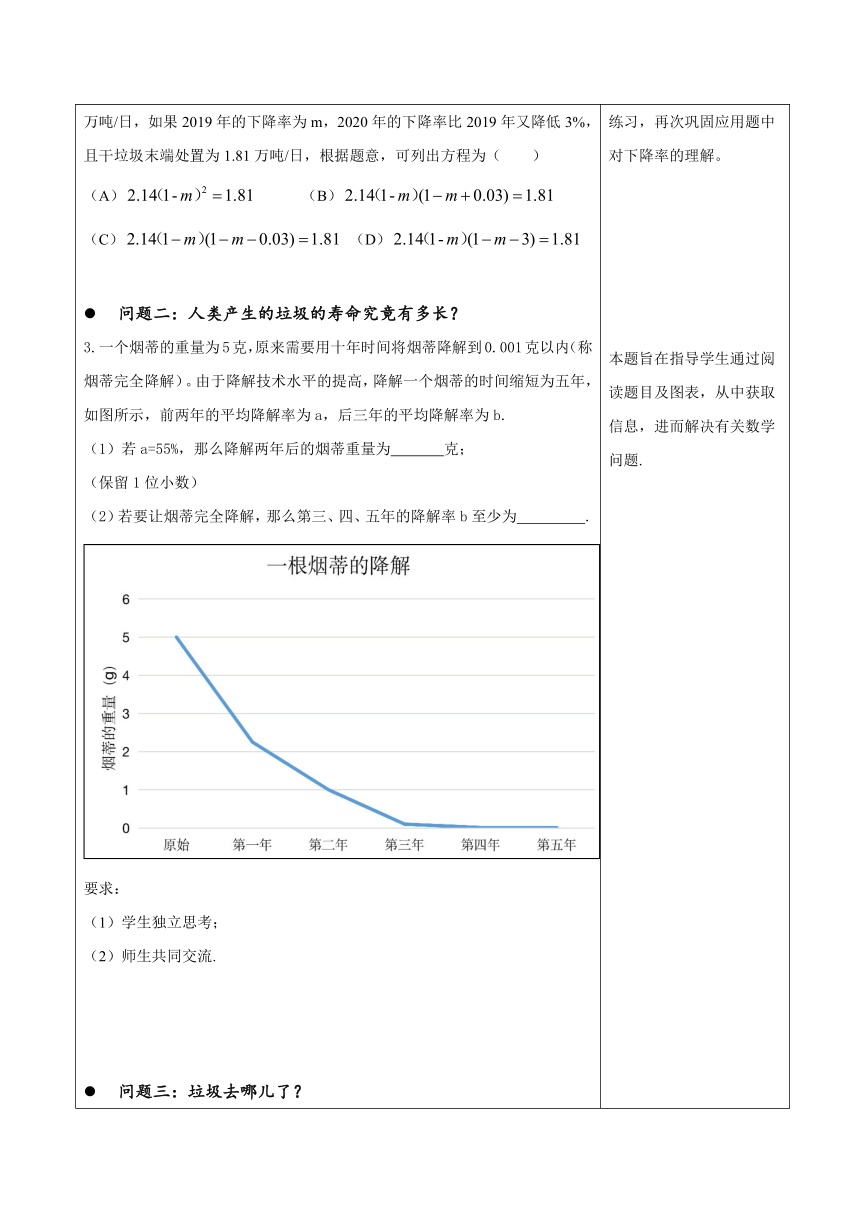
3.一个烟蒂的重量为5克,原来需要用十年时间将烟蒂降解到0.001克以内(称烟蒂完全降解)。由于降解技术水平的提高,降解一个烟蒂的时间缩短为五年,如图所示,前两年的平均降解率为a,后三年的平均降解率为b.
(1)若a=55%,那么降解两年后的烟蒂重量为
克;
(保留1位小数)
(2)若要让烟蒂完全降解,那么第三、四、五年的降解率b至少为
.
要求:
(1)学生独立思考;
(2)师生共同交流.
问题三:垃圾去哪儿了?
4.某垃圾场回收易拉罐,运送到铝制品加工厂,熔化后装在一个长方体的容器铸成长方体铝块,要切割成96个一样大小的小正方体铝块,若不计损耗,则该铝块恰好用完,没有剩余.
铝制品加工厂有两个不同的长方体容器:
容器一:长128厘米,宽128厘米,高24厘米的长方体容器;
容器二:长128厘米,宽64厘米,高48厘米的长方体容器;
若不计损耗,小正方体的棱长为多少?你会选择哪一个容器?
要求:
(1)学生独立思考;
(2)小组讨论交流;
(3)归纳实际问题中检验的注意点.
(备用题)
问题四:其他国家是怎么做的?
5.在德国超市门口前有一台24小时回收器,可用积攒的瓶子兑换现金.购买一瓶0.5欧元的矿泉水时,往往还需要支付0.25欧元的塑料瓶押金,购买一罐1.2欧元的可乐,还需要支付0.5欧元的易拉罐押金,Lisa共有10欧元,其中押金一次性需要支付3欧元,Lisa买了多少瓶矿泉水,多少罐可乐?
本题是关于增长率的应用题,根据题意可列出一元二次方程,指导学生对2.5和以及这个代数式含义的理解,并指导学生利用开平方法解方程并归纳解决应用题的一般步骤.
通过对两次不同下降率的练习,再次巩固应用题中对下降率的理解。
本题旨在指导学生通过阅读题目及图表,从中获取信息,进而解决有关数学问题.
本题是等积变形的问题,将书本例题改编为容器方案的选择,提出方程根检验的必要性与重要性.
建立二元一次方程组解决实际问题,通过题目感悟其他国家在垃圾分类上的先进理念,也为后续的长作业提供思路与思考.
课堂小结
1.回顾今天课堂中提出的四个关于垃圾分类的数学问题;
2.谈谈本节课你的收获与困惑.
作业布置
1.练习册
2.长作业:以小组为单位,提出有关垃圾分类的问题,尝试运用数学思想建立方程,设计方案合作解决.
阅读材料
中国台湾——垃圾收费
从2000年7月1日起,台北市实行垃圾处理费随袋征收政策,要求一般垃圾必须放入计费的垃圾袋,厨余垃圾和可回收垃圾免收处理费。这种垃圾处理费随袋征收的政策促使市民养成了减少产生垃圾和注意回收资源的习惯,因为一般垃圾越多,用的收费垃圾袋就越多,花的钱也就越多.
瑞士——需要进口垃圾的国家
瑞士被人们赞誉为“没有垃圾污染的国家”。瑞士的垃圾循环利用率很高,每年处理的垃圾总量约为365吨,其中10%的垃圾是从意大利北部和德国西部城市进口,进口垃圾中超过50%的垃圾被循环利用。瑞士全国设有1.5万个塑料瓶收集中心,平均每个居民每年送往收集中心的塑料瓶有100个;瑞士全国废电池的回收率超过66%;铝制品的回收利用率则约在90%以上。与瑞士类似,瑞典也拥有着全世界最先进的,运行稳定、排放无污染、能源转化率最高的环保垃圾处理厂,能将大量垃圾转化为热能和电能,为瑞典成千上万家庭供暖、供电。为此,瑞典每年都从周边的国家进口大量垃圾,将垃圾做成了一笔既赚钱又为国民生活创造福利的好生意。
日本—垃圾分类细致严苛
日本垃圾分类工作的细致严苛堪称世界之最。日本的生活垃圾主要分为可燃垃圾、不可燃垃圾、塑料瓶类、其他塑料、易拉罐、玻璃瓶、资源垃圾、大型垃圾八大类,而且每一个大的类别下面又包含着许多细致的类别。日本横滨市把垃圾更细分为十大类,给市民发放的垃圾分类手册长达27页,有条款518项之多举个例子,如果你在日本喝完矿泉水后想要扔掉手中的瓶子,走向垃圾桶就可以了吗?当然不行!你要把瓶子冲洗干净后去掉瓶盖,撕掉标签,再把瓶子压扁后放入指定回收点。在日本想要扔掉手中的牛奶盒也不是一件容易的事,你喝完牛奶后要把牛奶盒洗干净,将牛奶盒拆开整理平整之后再晾干才能投放.
教案设计说明:
基于“抛锚式”问题下的数学应用题教学的课堂案例
建构主义认为:“学习者想要达成有意义的学习,最好的办法就是让学习者到现实世界的真实环境中去感受、去体验,通过获取直接经验来学习。”确定这类思考的问题被形象的比喻为“抛锚”,当教学中的问题被确定了,那么整个教学内容和教学进程就如同一艘轮船被“锚”固定了,围绕“锚”精心设计问题。而本节课是沪教版教材八年级第二学期第二十一章《代数方程》中21.7列方程(组)解应用题,本节课以三条主线串联,首先,围绕“垃圾分类”这个“锚”提出了四个问题,再由列不同类型的整式方程解决问题,第三则是以“学习方法”为主线贯穿整堂课甚至整个单元。
以“引入垃圾分类”为“锚”,体现数学建模思想
本堂课由教师引领学生提出有关垃圾分类的四个问题并共同解决,在课的结尾再将课上的四个问题分别进行深化,多维度的进行启发思考,并通过阅读材料再次丰富学生关于垃圾分类的知识,最后用进才中学全国建模大赛一等奖的案例鼓励学生自主提出问题,并尝试建立模型进行方案的设计。启发学生“用数学的眼光观察世界,用数学的语言表达世界,用数学的思维思考世界”,将数学建模思想、数学学科的育人价值都渗透在应用题教学中。
以“建立整式方程”为基本模型,提高分析解决实际问题的能力
本节课是本单元的第一课时,主要针对通过列整式方程(组)解决简单的实际问题,书中共两个例题,例1是关于汽车折旧率的问题,是关于百分率问题的应用,在六年级和八年级第一学期学生都有涉及,但学生往往会陷入解百分率应用题的套路化,而本课则设计了关于百分率的不同形式,有常规的增长率,同时也出现了下降率与降解率,从以往模式化的相等的增长率变化为不同的下降率,从以往一次下降变为两次不相等降解率的下降,通过不断的变式将关于百分比的应用题进行深入的研究,理清其真正的含义。而针对本堂课根的检验在关于增长率根的正负的检验较为容易,而在第四题中x=16这个根的检验较为困难,所以将书本例题2进行改编,让学生自主去发现检验根的实际意义的必要性。
以“构建学习方法”为整体框架,形成应用题学习的思考路径
本堂课建立解应用题的一般学习步骤,通过课内问题解决强化学生思考路径,并在第一课时中,搭建本单元应用题学习框架,在后续的课时中在“审题”环节还会出现“工作总量、时间、效率”、“路程、速度、时间”、“图形面积”等类型,设元的技巧也会在后几节课中进行体现,本节课解决了关于整式方程(组)的应用题,而后还会有分式方程、无理方程、分式方程组等应用;在检验的过程中,本堂课关注实际问题的检验,而在后面的课时中还要检验增根等问题。站在单元视角,为学生搭建脚手架,提供思考路径,将知识结构化、系统化。
本课以垃圾分类为“锚”,逐层递进,盘旋上升,在“提出问题”中开始,在“提出问题”后结束。
(1)列方程(组)解应用题
教学目标:通过复习百分率的应用引出一元高次方程的应用题,体验列方程解应用题的一般方法与步骤;经历对“问题三”容器的选择的讨论,理解方程的根在实际问题中检验的重要性;经历“实际问题-建立方程-方程求解-解释应用”的过程,体会方程思想,感知数学模型思想;依托垃圾分类为背景,体会方程的应用价值,增强数学应用意识,透过数据强化垃圾分类的重要性.
教学重点:体验列整式方程解决简单实际问题的过程.
教学难点:会列方程(组)解决简单的实际问题.
教学过程
设计意图
情境引入
问题一:你知道你每天会生产多少垃圾吗?
1.随着我们的生活越来越便利、物品越来越丰富我们丢弃的生活垃圾也就变得越来越多.上海2017年平均每人每天产生近1千克垃圾,并以每年20%的平均速度在增长,那么到了2018年,上海平均每人每天生产近
千克生活垃圾.
由旧知增长率问题引入本节课,抛出以垃圾分类为故事背景的这个“锚”,开始整堂课的研究.
二、新知学习
2.上海市在2000年就成为国内首批生活垃圾分类收集试点城市,开展了许多垃圾分类的探索性工作。根据最新的《上海市生活垃圾全程分类体系建设行动》,上海市生活垃圾综合处理能力从2018年底的2.5万吨/日,提高到2020年底的3.025万吨/日,若每年的平均增长率相同,求这个平均增长率.
要求:
学生独立思考;
学生板眼交流;
师生共同归纳解应用题的一般步骤.
揭示课题:21.7(1)列方程解应用题
练习:“再生能源中心”为实现零填埋,在2018年干垃圾末端处置达到2.14万吨/日,如果2019年的下降率为m,2020年的下降率比2019年又降低3%,且干垃圾末端处置为1.81万吨/日,根据题意,可列出方程为(
)
(B)
(C)
(D)
问题二:人类产生的垃圾的寿命究竟有多长?
3.一个烟蒂的重量为5克,原来需要用十年时间将烟蒂降解到0.001克以内(称烟蒂完全降解)。由于降解技术水平的提高,降解一个烟蒂的时间缩短为五年,如图所示,前两年的平均降解率为a,后三年的平均降解率为b.
(1)若a=55%,那么降解两年后的烟蒂重量为
克;
(保留1位小数)
(2)若要让烟蒂完全降解,那么第三、四、五年的降解率b至少为
.
要求:
(1)学生独立思考;
(2)师生共同交流.
问题三:垃圾去哪儿了?
4.某垃圾场回收易拉罐,运送到铝制品加工厂,熔化后装在一个长方体的容器铸成长方体铝块,要切割成96个一样大小的小正方体铝块,若不计损耗,则该铝块恰好用完,没有剩余.
铝制品加工厂有两个不同的长方体容器:
容器一:长128厘米,宽128厘米,高24厘米的长方体容器;
容器二:长128厘米,宽64厘米,高48厘米的长方体容器;
若不计损耗,小正方体的棱长为多少?你会选择哪一个容器?
要求:
(1)学生独立思考;
(2)小组讨论交流;
(3)归纳实际问题中检验的注意点.
(备用题)
问题四:其他国家是怎么做的?
5.在德国超市门口前有一台24小时回收器,可用积攒的瓶子兑换现金.购买一瓶0.5欧元的矿泉水时,往往还需要支付0.25欧元的塑料瓶押金,购买一罐1.2欧元的可乐,还需要支付0.5欧元的易拉罐押金,Lisa共有10欧元,其中押金一次性需要支付3欧元,Lisa买了多少瓶矿泉水,多少罐可乐?
本题是关于增长率的应用题,根据题意可列出一元二次方程,指导学生对2.5和以及这个代数式含义的理解,并指导学生利用开平方法解方程并归纳解决应用题的一般步骤.
通过对两次不同下降率的练习,再次巩固应用题中对下降率的理解。
本题旨在指导学生通过阅读题目及图表,从中获取信息,进而解决有关数学问题.
本题是等积变形的问题,将书本例题改编为容器方案的选择,提出方程根检验的必要性与重要性.
建立二元一次方程组解决实际问题,通过题目感悟其他国家在垃圾分类上的先进理念,也为后续的长作业提供思路与思考.
课堂小结
1.回顾今天课堂中提出的四个关于垃圾分类的数学问题;
2.谈谈本节课你的收获与困惑.
作业布置
1.练习册
2.长作业:以小组为单位,提出有关垃圾分类的问题,尝试运用数学思想建立方程,设计方案合作解决.
阅读材料
中国台湾——垃圾收费
从2000年7月1日起,台北市实行垃圾处理费随袋征收政策,要求一般垃圾必须放入计费的垃圾袋,厨余垃圾和可回收垃圾免收处理费。这种垃圾处理费随袋征收的政策促使市民养成了减少产生垃圾和注意回收资源的习惯,因为一般垃圾越多,用的收费垃圾袋就越多,花的钱也就越多.
瑞士——需要进口垃圾的国家
瑞士被人们赞誉为“没有垃圾污染的国家”。瑞士的垃圾循环利用率很高,每年处理的垃圾总量约为365吨,其中10%的垃圾是从意大利北部和德国西部城市进口,进口垃圾中超过50%的垃圾被循环利用。瑞士全国设有1.5万个塑料瓶收集中心,平均每个居民每年送往收集中心的塑料瓶有100个;瑞士全国废电池的回收率超过66%;铝制品的回收利用率则约在90%以上。与瑞士类似,瑞典也拥有着全世界最先进的,运行稳定、排放无污染、能源转化率最高的环保垃圾处理厂,能将大量垃圾转化为热能和电能,为瑞典成千上万家庭供暖、供电。为此,瑞典每年都从周边的国家进口大量垃圾,将垃圾做成了一笔既赚钱又为国民生活创造福利的好生意。
日本—垃圾分类细致严苛
日本垃圾分类工作的细致严苛堪称世界之最。日本的生活垃圾主要分为可燃垃圾、不可燃垃圾、塑料瓶类、其他塑料、易拉罐、玻璃瓶、资源垃圾、大型垃圾八大类,而且每一个大的类别下面又包含着许多细致的类别。日本横滨市把垃圾更细分为十大类,给市民发放的垃圾分类手册长达27页,有条款518项之多举个例子,如果你在日本喝完矿泉水后想要扔掉手中的瓶子,走向垃圾桶就可以了吗?当然不行!你要把瓶子冲洗干净后去掉瓶盖,撕掉标签,再把瓶子压扁后放入指定回收点。在日本想要扔掉手中的牛奶盒也不是一件容易的事,你喝完牛奶后要把牛奶盒洗干净,将牛奶盒拆开整理平整之后再晾干才能投放.
教案设计说明:
基于“抛锚式”问题下的数学应用题教学的课堂案例
建构主义认为:“学习者想要达成有意义的学习,最好的办法就是让学习者到现实世界的真实环境中去感受、去体验,通过获取直接经验来学习。”确定这类思考的问题被形象的比喻为“抛锚”,当教学中的问题被确定了,那么整个教学内容和教学进程就如同一艘轮船被“锚”固定了,围绕“锚”精心设计问题。而本节课是沪教版教材八年级第二学期第二十一章《代数方程》中21.7列方程(组)解应用题,本节课以三条主线串联,首先,围绕“垃圾分类”这个“锚”提出了四个问题,再由列不同类型的整式方程解决问题,第三则是以“学习方法”为主线贯穿整堂课甚至整个单元。
以“引入垃圾分类”为“锚”,体现数学建模思想
本堂课由教师引领学生提出有关垃圾分类的四个问题并共同解决,在课的结尾再将课上的四个问题分别进行深化,多维度的进行启发思考,并通过阅读材料再次丰富学生关于垃圾分类的知识,最后用进才中学全国建模大赛一等奖的案例鼓励学生自主提出问题,并尝试建立模型进行方案的设计。启发学生“用数学的眼光观察世界,用数学的语言表达世界,用数学的思维思考世界”,将数学建模思想、数学学科的育人价值都渗透在应用题教学中。
以“建立整式方程”为基本模型,提高分析解决实际问题的能力
本节课是本单元的第一课时,主要针对通过列整式方程(组)解决简单的实际问题,书中共两个例题,例1是关于汽车折旧率的问题,是关于百分率问题的应用,在六年级和八年级第一学期学生都有涉及,但学生往往会陷入解百分率应用题的套路化,而本课则设计了关于百分率的不同形式,有常规的增长率,同时也出现了下降率与降解率,从以往模式化的相等的增长率变化为不同的下降率,从以往一次下降变为两次不相等降解率的下降,通过不断的变式将关于百分比的应用题进行深入的研究,理清其真正的含义。而针对本堂课根的检验在关于增长率根的正负的检验较为容易,而在第四题中x=16这个根的检验较为困难,所以将书本例题2进行改编,让学生自主去发现检验根的实际意义的必要性。
以“构建学习方法”为整体框架,形成应用题学习的思考路径
本堂课建立解应用题的一般学习步骤,通过课内问题解决强化学生思考路径,并在第一课时中,搭建本单元应用题学习框架,在后续的课时中在“审题”环节还会出现“工作总量、时间、效率”、“路程、速度、时间”、“图形面积”等类型,设元的技巧也会在后几节课中进行体现,本节课解决了关于整式方程(组)的应用题,而后还会有分式方程、无理方程、分式方程组等应用;在检验的过程中,本堂课关注实际问题的检验,而在后面的课时中还要检验增根等问题。站在单元视角,为学生搭建脚手架,提供思考路径,将知识结构化、系统化。
本课以垃圾分类为“锚”,逐层递进,盘旋上升,在“提出问题”中开始,在“提出问题”后结束。
