京改版八年级上册12.5全等三角形的判定(4) 教学设计(表格式)
文档属性
| 名称 | 京改版八年级上册12.5全等三角形的判定(4) 教学设计(表格式) |
|
|
| 格式 | zip | ||
| 文件大小 | 79.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 19:38:35 | ||
图片预览


文档简介
课程基本信息
课题
全等三角形的判定(4)
教科书
书名:义务教育教科书
数学
八年级上册
出版社:北京出版社
出版日期:
2014年7月
教学目标
教学目标:能灵活运用全等三角形的判定及性质,解决简单问题.
教学重点:能正确根据条件判定三角形全等,能利用三角形全等推出所需的结论.
教学难点:能利用全等三角形建立已知与所求的联系.
教学过程
时间
教学环节
主要师生活动
1′20″
复习引入
全等三角形的判定:
1.有三边分别相等的两个三角形全等(SSS);
2.有两边和它们的夹角分别相等的两个三角形全等(SAS);
3.有两角和它们的夹边分别相等的两个三角形全等(ASA);
4.有两个角及其中一个角的对边分别相等的两个三角形全等(AAS).
小结:判定三角形全等必须具备三个条件,且至少有一个条件为边.
12′30″
例题讲解
例
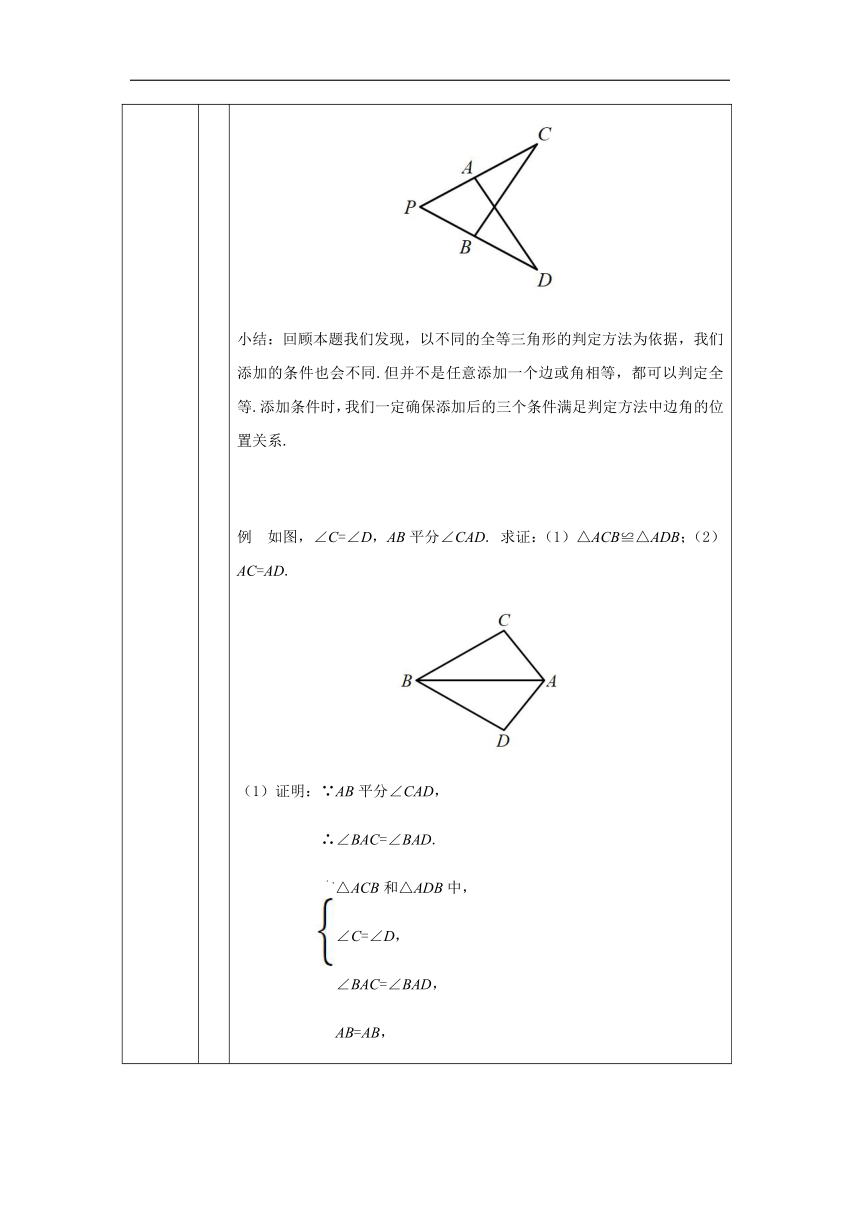
如图,PA=PB,如果再添加一个条件,可以直接判定△PAD≌△PBC,
那么该条件可以是PD=PC(或∠PAD=∠PBC或∠D=∠C).
小结:回顾本题我们发现,以不同的全等三角形的判定方法为依据,我们添加的条件也会不同.但并不是任意添加一个边或角相等,都可以判定全等.添加条件时,我们一定确保添加后的三个条件满足判定方法中边角的位置关系.
例
如图,∠C=∠D,AB平分∠CAD.
求证:(1)△ACB≌△ADB;(2)AC=AD.
(1)证明:∵AB平分∠CAD,
∴∠BAC=∠BAD.
在△ACB和△ADB中,
∠C=∠D,
∠BAC=∠BAD,
AB=AB,
∴△ACB≌△ADB(AAS).
(2)证明:∵△ACB≌△ADB,
∴AC=AD(全等三角形对应边相等).
小结:运用全等三角形的判定及性质,我们以三个边或角相等为条件,可以推证出余下三个边或角相等的结论.
例
如图,△ABC中,点D为BC中点,BE⊥AD的延长线于E,CF⊥AD于F.
求证:BE=CF.
证明:∵点D为BC中点,
∴BD=CD.
∵BE⊥AD,CF⊥AD,
∴∠E=∠CFD=90°.
在△BDE和△CDF中,
∠E=∠CFD,
∠BDE=∠CDF,
BD=CD,
∴△BDE≌△CDF(AAS).
∴BE=CF(全等三角形对应边相等).
例
如图,三角形钢架中,AB=AC,AD是连接点A与BC中点D的支架.∠BAD与∠CAD相等吗?为什么?
已知:如图,在△ABC中,AB=AC,AD是边BC上的中线.判断∠BAD与∠CAD的数量关系,并说明理由.
解:∠BAD与∠CAD的数量关系为∠BAD=∠CAD.
∵AD是边BC上的中线,
∴BD=CD.
在△ABD和△ACD中,
AB=AC,
BD=CD,
AD=AD,
∴△ABD≌△ACD(SSS).
∴∠BAD=∠CAD(全等三角形对应角相等).
小结:在解决实际问题时,我们应先将其转为数学问题,之后再利用我们掌握的数学知识解决问题.
例
如图,E,C是BF上两点,且BE=CF,AB=DE,AC=DF.
求证:AB∥DE,AC∥DF.
证明:∵BE=CF,
∴BE+EC=CF+EC.
即BC=EF.
在△ABC和△DEF中,
BC=EF,
AB=DE,
AC=DF,
∴△ABC≌△DEF(SSS).
∴∠B=∠DEF,∠ACB=∠F(全等三角形对应角相等).
∴AB∥DE,AC∥DF.
小结:通过本题的分析,可以看到,当条件充足时,我们可以先判定两个三角形全等.再根据全等三角形的性质得到新的结论.最后利用这些结论来完成的证明.
2′10″
回顾小结
数学知识:
全等三角形的判定:
1.有三边分别相等的两个三角形全等(SSS);
2.有两边和它们的夹角分别相等的两个三角形全等(SAS);
3.有两角和它们的夹边分别相等的两个三角形全等(ASA);
4.有两个角及其中一个角的对边分别相等的两个三角形全等(AAS).
全等三角形的性质:
1.全等三角形对应边相等;2.全等三角形对应角相等.
解题方法:
10″
课后作业
1.如图,△ABC中,∠B=∠C,AD⊥BC于D.
求证:BD=CD.
2.如图,C为BE中点,AB∥DC,AB=DC.
求证:∠A=∠D.
课题
全等三角形的判定(4)
教科书
书名:义务教育教科书
数学
八年级上册
出版社:北京出版社
出版日期:
2014年7月
教学目标
教学目标:能灵活运用全等三角形的判定及性质,解决简单问题.
教学重点:能正确根据条件判定三角形全等,能利用三角形全等推出所需的结论.
教学难点:能利用全等三角形建立已知与所求的联系.
教学过程
时间
教学环节
主要师生活动
1′20″
复习引入
全等三角形的判定:
1.有三边分别相等的两个三角形全等(SSS);
2.有两边和它们的夹角分别相等的两个三角形全等(SAS);
3.有两角和它们的夹边分别相等的两个三角形全等(ASA);
4.有两个角及其中一个角的对边分别相等的两个三角形全等(AAS).
小结:判定三角形全等必须具备三个条件,且至少有一个条件为边.
12′30″
例题讲解
例
如图,PA=PB,如果再添加一个条件,可以直接判定△PAD≌△PBC,
那么该条件可以是PD=PC(或∠PAD=∠PBC或∠D=∠C).
小结:回顾本题我们发现,以不同的全等三角形的判定方法为依据,我们添加的条件也会不同.但并不是任意添加一个边或角相等,都可以判定全等.添加条件时,我们一定确保添加后的三个条件满足判定方法中边角的位置关系.
例
如图,∠C=∠D,AB平分∠CAD.
求证:(1)△ACB≌△ADB;(2)AC=AD.
(1)证明:∵AB平分∠CAD,
∴∠BAC=∠BAD.
在△ACB和△ADB中,
∠C=∠D,
∠BAC=∠BAD,
AB=AB,
∴△ACB≌△ADB(AAS).
(2)证明:∵△ACB≌△ADB,
∴AC=AD(全等三角形对应边相等).
小结:运用全等三角形的判定及性质,我们以三个边或角相等为条件,可以推证出余下三个边或角相等的结论.
例
如图,△ABC中,点D为BC中点,BE⊥AD的延长线于E,CF⊥AD于F.
求证:BE=CF.
证明:∵点D为BC中点,
∴BD=CD.
∵BE⊥AD,CF⊥AD,
∴∠E=∠CFD=90°.
在△BDE和△CDF中,
∠E=∠CFD,
∠BDE=∠CDF,
BD=CD,
∴△BDE≌△CDF(AAS).
∴BE=CF(全等三角形对应边相等).
例
如图,三角形钢架中,AB=AC,AD是连接点A与BC中点D的支架.∠BAD与∠CAD相等吗?为什么?
已知:如图,在△ABC中,AB=AC,AD是边BC上的中线.判断∠BAD与∠CAD的数量关系,并说明理由.
解:∠BAD与∠CAD的数量关系为∠BAD=∠CAD.
∵AD是边BC上的中线,
∴BD=CD.
在△ABD和△ACD中,
AB=AC,
BD=CD,
AD=AD,
∴△ABD≌△ACD(SSS).
∴∠BAD=∠CAD(全等三角形对应角相等).
小结:在解决实际问题时,我们应先将其转为数学问题,之后再利用我们掌握的数学知识解决问题.
例
如图,E,C是BF上两点,且BE=CF,AB=DE,AC=DF.
求证:AB∥DE,AC∥DF.
证明:∵BE=CF,
∴BE+EC=CF+EC.
即BC=EF.
在△ABC和△DEF中,
BC=EF,
AB=DE,
AC=DF,
∴△ABC≌△DEF(SSS).
∴∠B=∠DEF,∠ACB=∠F(全等三角形对应角相等).
∴AB∥DE,AC∥DF.
小结:通过本题的分析,可以看到,当条件充足时,我们可以先判定两个三角形全等.再根据全等三角形的性质得到新的结论.最后利用这些结论来完成的证明.
2′10″
回顾小结
数学知识:
全等三角形的判定:
1.有三边分别相等的两个三角形全等(SSS);
2.有两边和它们的夹角分别相等的两个三角形全等(SAS);
3.有两角和它们的夹边分别相等的两个三角形全等(ASA);
4.有两个角及其中一个角的对边分别相等的两个三角形全等(AAS).
全等三角形的性质:
1.全等三角形对应边相等;2.全等三角形对应角相等.
解题方法:
10″
课后作业
1.如图,△ABC中,∠B=∠C,AD⊥BC于D.
求证:BD=CD.
2.如图,C为BE中点,AB∥DC,AB=DC.
求证:∠A=∠D.
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
