华东师大版七年级数学下册 第十章 轴对称、平移与旋转 单元检测试题(word解析版)
文档属性
| 名称 | 华东师大版七年级数学下册 第十章 轴对称、平移与旋转 单元检测试题(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 276.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 22:57:50 | ||
图片预览


文档简介
第十章
轴对称、平移与旋转
单元检测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
8
小题
,每题
3
分
,共计24分
,
)
?
1.
将等边绕自身的内心,顺时针至少旋转,就能与自身重合,则等于(
)
A.
B.
C.
D.
?
2.
下面所描述图形中既是轴对称图形又是中心对称图形的是(?
?
?
?
)
A.等腰直角三角形
B.平行四边形
C.等边三角形
D.正方形
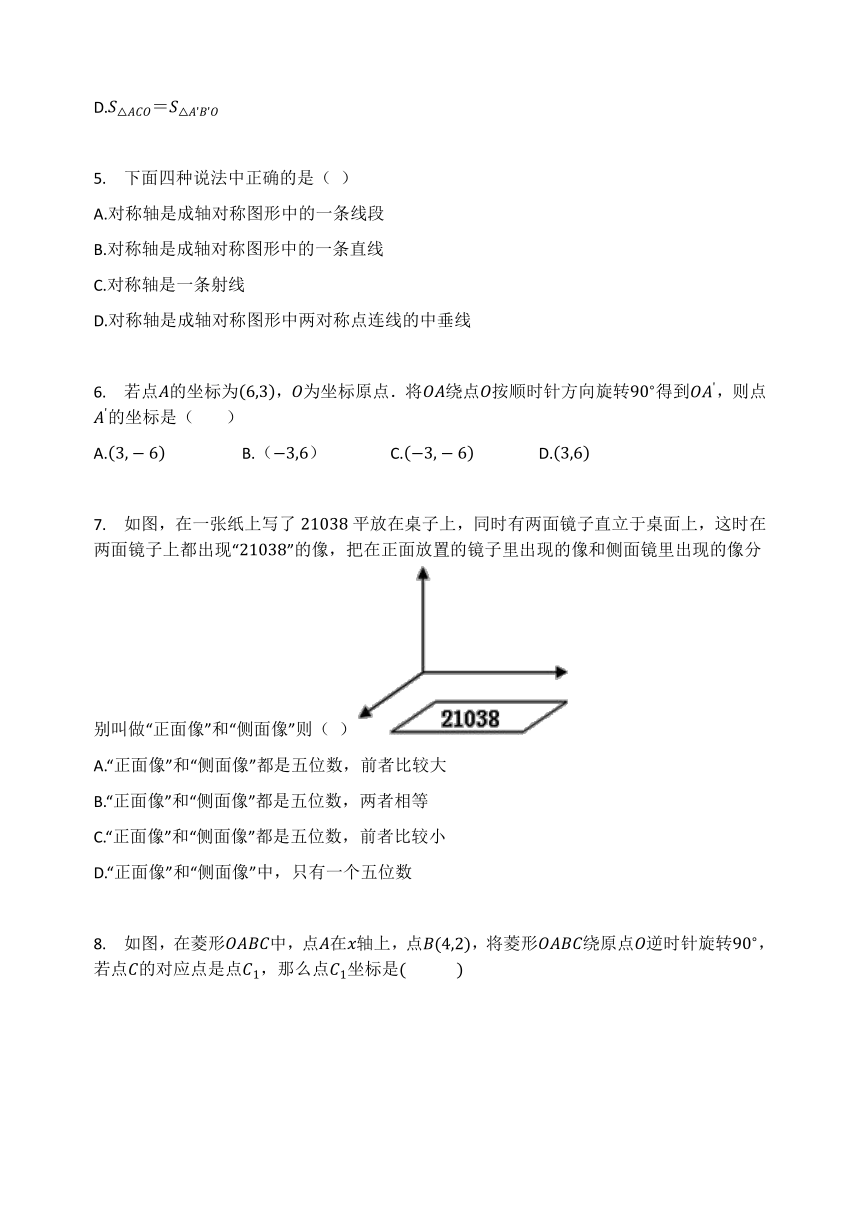
3.
如图,在已知的中,按以下步骤作图:①分别以点为圆心、大于的长为半径作弧,两弧相交于点,;②作直线,交于点,连结.若
,则下列结论中错误的是(?
?
?
?
)
A.
B.
C.点为??的外心?
D.
4.
如图,与是成中心对称,下列说法不正确的是(
)
A.=
B.=,=,=
C.,,
D.=
?
5.
下面四种说法中正确的是(
)
A.对称轴是成轴对称图形中的一条线段
B.对称轴是成轴对称图形中的一条直线
C.对称轴是一条射线
D.对称轴是成轴对称图形中两对称点连线的中垂线
?
6.
若点的坐标为,为坐标原点.将绕点按顺时针方向旋转得到,则点的坐标是(????????)
A.
B.()
C.
D.
?
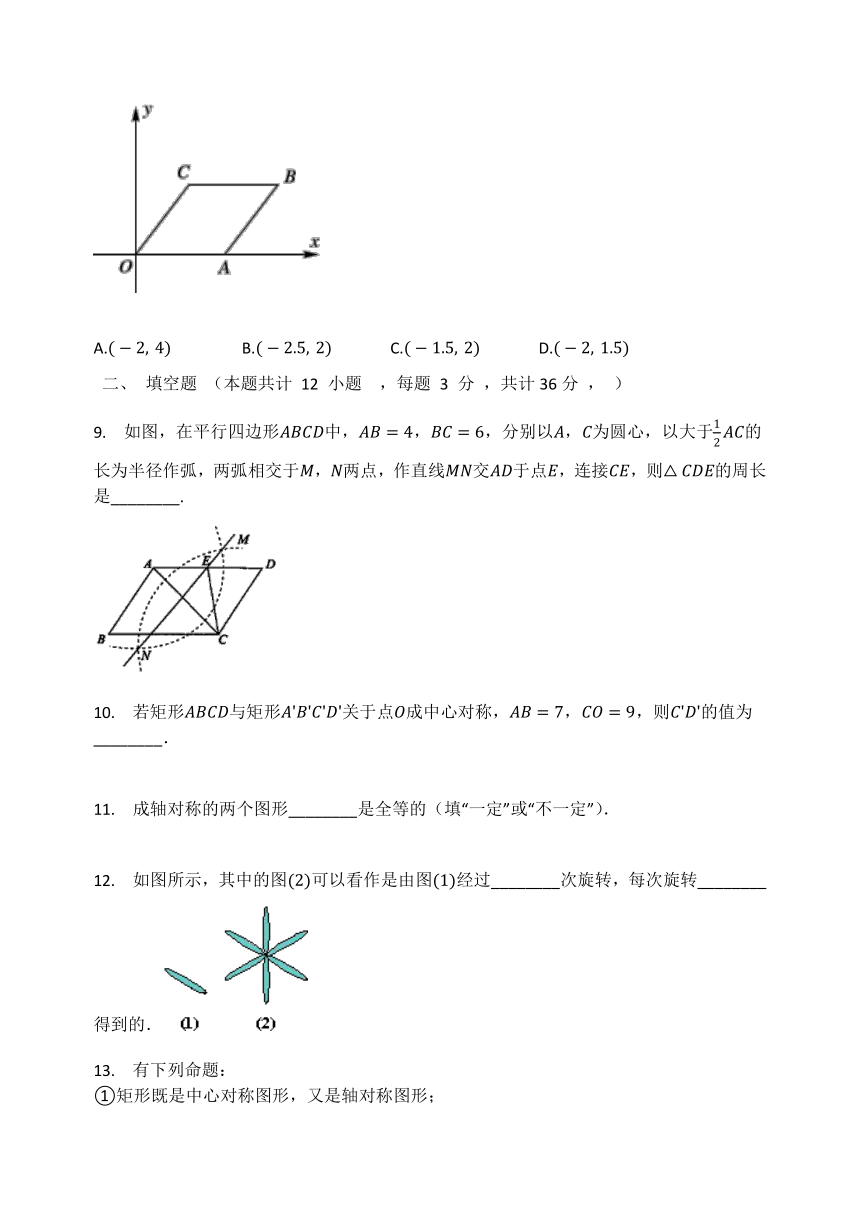
7.
如图,在一张纸上写了平放在桌子上,同时有两面镜子直立于桌面上,这时在两面镜子上都出现“”的像,把在正面放置的镜子里出现的像和侧面镜里出现的像分别叫做“正面像”和“侧面像”则(
)
A.“正面像”和“侧面像”都是五位数,前者比较大
B.“正面像”和“侧面像”都是五位数,两者相等
C.“正面像”和“侧面像”都是五位数,前者比较小
D.“正面像”和“侧面像”中,只有一个五位数
?
8.
如图,在菱形中,点在轴上,点,将菱形绕原点逆时针旋转,若点的对应点是点,那么点坐标是?
?
?
?
A.
B.
C.
D.
二、
填空题
(本题共计
12
小题
,每题
3
分
,共计36分
,
)
9.
如图,在平行四边形中,,,分别以,为圆心,以大于的长为半径作弧,两弧相交于,两点,作直线交于点,连接,则的周长是________.
10.
若矩形与矩形关于点成中心对称,,,则的值为________.
?
11.
成轴对称的两个图形________是全等的(填“一定”或“不一定”).
?
12.
如图所示,其中的图可以看作是由图经过________次旋转,每次旋转________得到的.
?
13.
有下列命题:
①矩形既是中心对称图形,又是轴对称图形;?
②平行四边形是中心对称图形,不是轴对称图形;
④等腰梯形是轴对称图形,不是中心对称图形;
④有一个锐角是的直角三角形不是中心对称图形,也不是轴对称图形.
其中正确命题的序号是________.(把所有正确的命题的序号都填上)
?
14.
如图,是的平分线,请你利用该图形,用三角板和圆规画一对以所在直线为对称轴的全等三角形,并标注字母.你画的是________________,依据是________.
?
15.
如图是“北大西洋公约组织”标志的主体部(平面图),它是由四边形绕点进行次旋转变换后形成的.测得,,,则的度数是________.
?
16.
如果,的周长是,,.,则________.
?
17.
四个单位正方形以边对边方式相连接而成,可以拼成如图的五种不同形状.用一片“”形(图中第一个)分别于其余四个中的一片拼成轴对称图形,所有的可能共有________种.
?18.
如图,,,,在、上分别找一点、,当周长最小时,的度数为________度.
?
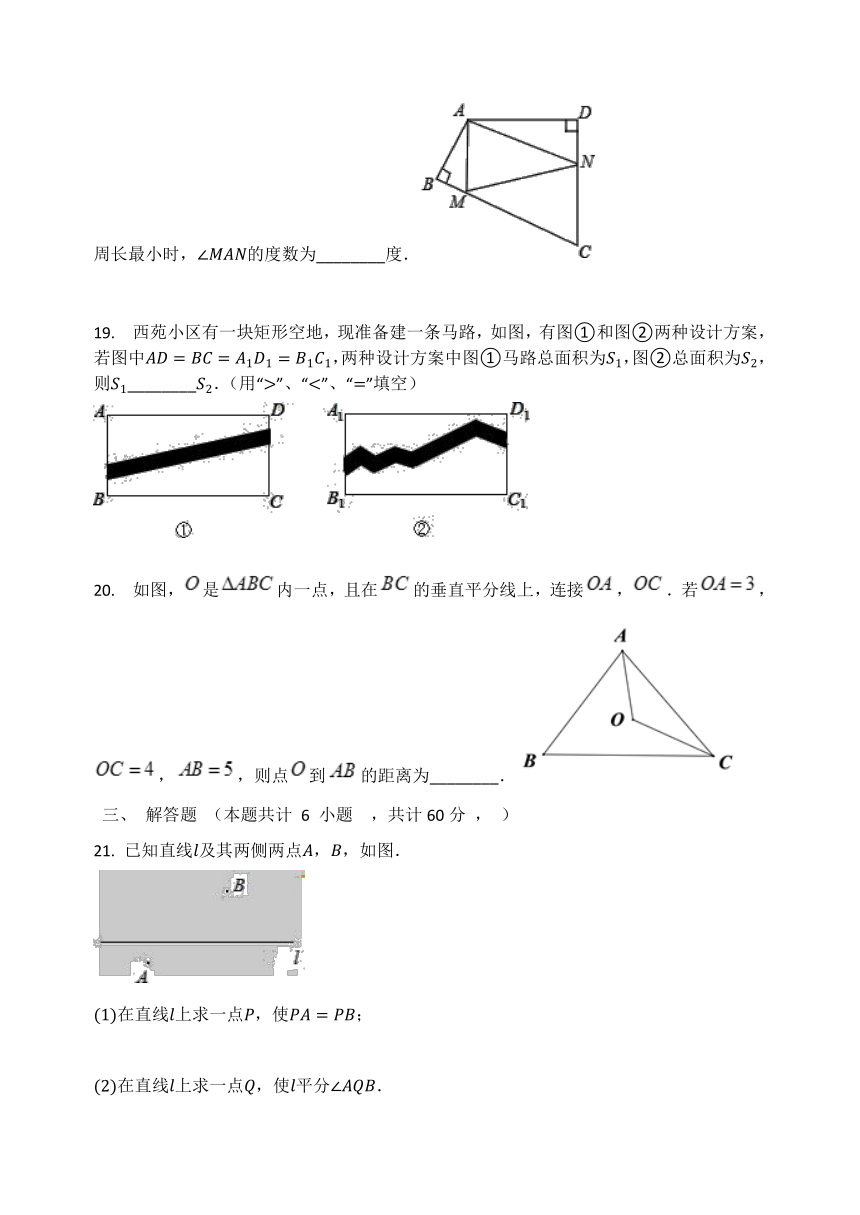
19.
西苑小区有一块矩形空地,现准备建一条马路,如图,有图①和图②两种设计方案,若图中,两种设计方案中图①马路总面积为,图②总面积为,则________.(用“”、“”、“”填空)
?
20.
如图,是内一点,且在的垂直平分线上,连接,.若,,,则点到的距离为________.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
已知直线及其两侧两点,,如图.
在直线上求一点,使;
在直线上求一点,使平分.
(以上两小题保留作图痕迹,标出必要的字母,不要求写作法)
?
22.
如图,点、在直线的同侧,点是点关于的对称点,交于点.
(1)与相等吗?为什么?
(2)在上再取一点,并连接和,比较与的大小,并说明理由.
?
23.
如图,在四边形中,,,,画出线段平移后的线段,其平移方向为射线的方向,平移距离为的长,平移后所得的线段与相交于.线段与线段相等吗?与相等吗?与相等吗?与相等吗?试说明理由.
?
24.
如图所示,已知四边形和过点的直线,求作四边形,使四边形与四边形关于直线对称.
?
25.
设直线和直线平行,且和间的距离为.如果线段在的右侧,并设关于的对称图形是,而关于的对称图形是″″(如图),那么,线段和″″有什么关系?
?
26.
如图,将三角形沿射线方向平移到三角形的位置,连接.
(1)与的位置关系为________;
(2)求证:=;
(3)设=,=,试探索与,之间的数量关系,并证明你的结论.
参考答案
一、
选择题
(本题共计
8
小题
,每题
3
分
,共计24分
)
1.
【答案】
B
【解答】
解:因为等边三角形的外心到三个顶点的距离相等,相邻顶点与外心连线的夹角相等,
所以,,即每次至少旋转.
故选:.
2.
【答案】
D
【解答】
解:如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形;
如果把一个图形绕着某一点旋转,它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称.
,∵
此图形旋转后不能与原图形重合,
∴
此图形不是中心对称图形,是轴对称图形,故此选项错误;
,此图形旋转后能与原图形重合,
∴
此图形是中心对称图形,不是轴对称图形,故此选项错误;
,∵
此图形旋转后不能与原图形重合,
∴
此图形不是中心对称图形,是轴对称图形,故此选项错误;
,∵
此图形旋转后能与原图形重合,
∴
此图形是中心对称图形,且是轴对称图形,故此选项正确.
故选.
3.
【答案】
A
【解答】
解:由题意可知直线是线段的垂直平分线,
∴
.∵
,
∴
,
∴
.
∵
,
∴
,
故选项中的结论错误,选项中的结论正确.
∵
,
∴
,
∴
点为的外心,故选项中的结论正确,
∵
?,,
∴
,故选项中的结论正确.
故选.
4.
【答案】
D
【解答】
、根据中心对称的两个图形全等,即可得到,故正确;
、根据中心对称的两个图形全等,即可得到,故正确;
、根对称点到对称中心的距离相等,即可证得对应线段平行,故正确;
、不正确.
5.
【答案】
D
【解答】
解:∵
对称轴是成轴对称图形中任何一对对应点所连线段的垂直平分线,故本选项错误;
∴
、、错误,正确.
故选.
6.
【答案】
A
【解答】
略
7.
【答案】
D
【解答】
解:根据镜面对称的性质,“”和“”关于镜面对称,“”、“”、“”、“”在镜中的成像还是原数,
则数码“”在正面镜子中的像是,在侧面镜子中的像不是一个位数,
即可得“正面像”和“侧面像”中,只有一个五位数.
故选.
8.
【答案】
D
【解答】
解:如图所示:
过点作于,过点作于,过点作于,
根据旋转的性质可知,,,
∵
四边形是菱形,点,
∴
,,即;
设点坐标为,根据菱形的边长相等可得,
则,解得,
即,
通过旋转图知,此时点落在第二象限,
则点的坐标为.
故选.
二、
填空题
(本题共计
12
小题
,每题
3
分
,共计36分
)
9.
【答案】
【解答】
解:利用作图得垂直平分,
∴
,
∴
的周长
,
∵
四边形为平行四边形,
∴
,,
∴
的周长.
故答案为:.
10.
【答案】
【解答】
解:∵
矩形与矩形关于点成中心对称,
∴
.
故答案为:.
11.
【答案】
一定
【解答】
成轴对称的两个图形一定是全等的.
12.
【答案】
,
【解答】
解:由个图形组成,所以,
故可以看成由一个图形经过次旋转得到的,
每次分别旋转了.
故答案为:,.
13.
【答案】
①②③④
【解答】
解:①矩形既是中心对称图形,又是轴对称图形,正确;
②平行四边形是中心对称图形,不是轴对称图形,正确;
③等腰梯形是轴对称图形,不是中心对称图形,正确;
④有一个锐角是的直角三角形不是中心对称图形,也不是轴对称图形,正确;
综上可得①②③④都正确.
故答案为①②③④.
14.
【答案】
,,
【解答】
解:作图过程:以为圆心任意长为半径作弧,交射线,为,两点,在射线上任取一点(点除外),连接,,
所得,
∵
,是公共边,是角平分线,
∴
全等的依据是.
15.
【答案】
【解答】
解:∵
“北大西洋公约组织”标志的主体部分(平面图)是由四边形绕点进行次旋转变换后形成的,
∴
.
在和中
,
∴
,
∴
,.
即,.
在中,.
故答案为:.
16.
【答案】
【解答】
解:.
∵
,,
∴
.
故答案为:.
17.
【答案】
【解答】
解:将分别与各图形组合能满足组合后是轴对称的有:
,
共种.
故答案为:.
18.
【答案】
【解答】
解:作关于和的对称点,″,连接″,交于,交于,则″即为的周长最小值,作延长线,.
∵
,
∴
,
∴
″,
∵
,″,
∴
,
∴
,
故答案为:.
19.
【答案】
【解答】
解:设马路宽为,
由题意可得出:,,
故.
故答案为:.
20.
【答案】
、,
【解答】
解:如图,连接.过点作于.
“
○在的垂直平分线上,
&
为直角三角形,
故答案为
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
解:如图所示,点即为所求.
如中图所示,点即为所求.
【解答】
解:如图所示,点即为所求.
如中图所示,点即为所求.
22.
【答案】
解:(1)与相等,连接,
∵
点是点关于的对称点,
∴
垂直平分线段,
∴
,
∴
,
即:;
(2),
连接,如图所示,
∵
点是点关于的对称点,
∴
垂直平分线段,
∴
,
∵
,
∴
,
∵
,
∴
.
【解答】
解:(1)与相等,连接,
∵
点是点关于的对称点,
∴
垂直平分线段,
∴
,
∴
,
即:;
(2),
连接,如图所示,
∵
点是点关于的对称点,
∴
垂直平分线段,
∴
,
∵
,
∴
,
∵
,
∴
.
23.
【答案】
解:平移后的图形如下所示:
由题意可知:四边形是等腰梯形,
∴
,,
又是由平移得到的,故,,
∴
..
【解答】
解:平移后的图形如下所示:
由题意可知:四边形是等腰梯形,
∴
,,
又是由平移得到的,故,,
∴
..
24.
【答案】
解:如图所示:
.
【解答】
解:如图所示:
.
25.
【答案】
解:因为平行于,并且″垂直于,当然也垂直于,同理″也垂直于和.
又在平面内垂直于同一条直线的两条直线互相平行,
所以″″.①
另一方面,因为,″,
所以″,
同理″,
所以″″.②
由①②可知,为平行四边形,所以平行且等于.
【解答】
解:因为平行于,并且″垂直于,当然也垂直于,同理″也垂直于和.
又在平面内垂直于同一条直线的两条直线互相平行,
所以″″.①
另一方面,因为,″,
所以″,
同理″,
所以″″.②
由①②可知,为平行四边形,所以平行且等于.
26.
【答案】
根据平移性质可知,,
∴
=,=,
∴
=,
∴
=,
结论:=,
过点作,交于点,
根据平移性质可知,
∴
,
∴
=,=,
∴
===,
即=.
【解答】
由平移的性质可得:;
故答案为:;
根据平移性质可知,,
∴
=,=,
∴
=,
∴
=,
结论:=,
过点作,交于点,
根据平移性质可知,
∴
,
∴
=,=,
∴
===,
即=.
轴对称、平移与旋转
单元检测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
8
小题
,每题
3
分
,共计24分
,
)
?
1.
将等边绕自身的内心,顺时针至少旋转,就能与自身重合,则等于(
)
A.
B.
C.
D.
?
2.
下面所描述图形中既是轴对称图形又是中心对称图形的是(?
?
?
?
)
A.等腰直角三角形
B.平行四边形
C.等边三角形
D.正方形
3.
如图,在已知的中,按以下步骤作图:①分别以点为圆心、大于的长为半径作弧,两弧相交于点,;②作直线,交于点,连结.若
,则下列结论中错误的是(?
?
?
?
)
A.
B.
C.点为??的外心?
D.
4.
如图,与是成中心对称,下列说法不正确的是(
)
A.=
B.=,=,=
C.,,
D.=
?
5.
下面四种说法中正确的是(
)
A.对称轴是成轴对称图形中的一条线段
B.对称轴是成轴对称图形中的一条直线
C.对称轴是一条射线
D.对称轴是成轴对称图形中两对称点连线的中垂线
?
6.
若点的坐标为,为坐标原点.将绕点按顺时针方向旋转得到,则点的坐标是(????????)
A.
B.()
C.
D.
?
7.
如图,在一张纸上写了平放在桌子上,同时有两面镜子直立于桌面上,这时在两面镜子上都出现“”的像,把在正面放置的镜子里出现的像和侧面镜里出现的像分别叫做“正面像”和“侧面像”则(
)
A.“正面像”和“侧面像”都是五位数,前者比较大
B.“正面像”和“侧面像”都是五位数,两者相等
C.“正面像”和“侧面像”都是五位数,前者比较小
D.“正面像”和“侧面像”中,只有一个五位数
?
8.
如图,在菱形中,点在轴上,点,将菱形绕原点逆时针旋转,若点的对应点是点,那么点坐标是?
?
?
?
A.
B.
C.
D.
二、
填空题
(本题共计
12
小题
,每题
3
分
,共计36分
,
)
9.
如图,在平行四边形中,,,分别以,为圆心,以大于的长为半径作弧,两弧相交于,两点,作直线交于点,连接,则的周长是________.
10.
若矩形与矩形关于点成中心对称,,,则的值为________.
?
11.
成轴对称的两个图形________是全等的(填“一定”或“不一定”).
?
12.
如图所示,其中的图可以看作是由图经过________次旋转,每次旋转________得到的.
?
13.
有下列命题:
①矩形既是中心对称图形,又是轴对称图形;?
②平行四边形是中心对称图形,不是轴对称图形;
④等腰梯形是轴对称图形,不是中心对称图形;
④有一个锐角是的直角三角形不是中心对称图形,也不是轴对称图形.
其中正确命题的序号是________.(把所有正确的命题的序号都填上)
?
14.
如图,是的平分线,请你利用该图形,用三角板和圆规画一对以所在直线为对称轴的全等三角形,并标注字母.你画的是________________,依据是________.
?
15.
如图是“北大西洋公约组织”标志的主体部(平面图),它是由四边形绕点进行次旋转变换后形成的.测得,,,则的度数是________.
?
16.
如果,的周长是,,.,则________.
?
17.
四个单位正方形以边对边方式相连接而成,可以拼成如图的五种不同形状.用一片“”形(图中第一个)分别于其余四个中的一片拼成轴对称图形,所有的可能共有________种.
?18.
如图,,,,在、上分别找一点、,当周长最小时,的度数为________度.
?
19.
西苑小区有一块矩形空地,现准备建一条马路,如图,有图①和图②两种设计方案,若图中,两种设计方案中图①马路总面积为,图②总面积为,则________.(用“”、“”、“”填空)
?
20.
如图,是内一点,且在的垂直平分线上,连接,.若,,,则点到的距离为________.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
已知直线及其两侧两点,,如图.
在直线上求一点,使;
在直线上求一点,使平分.
(以上两小题保留作图痕迹,标出必要的字母,不要求写作法)
?
22.
如图,点、在直线的同侧,点是点关于的对称点,交于点.
(1)与相等吗?为什么?
(2)在上再取一点,并连接和,比较与的大小,并说明理由.
?
23.
如图,在四边形中,,,,画出线段平移后的线段,其平移方向为射线的方向,平移距离为的长,平移后所得的线段与相交于.线段与线段相等吗?与相等吗?与相等吗?与相等吗?试说明理由.
?
24.
如图所示,已知四边形和过点的直线,求作四边形,使四边形与四边形关于直线对称.
?
25.
设直线和直线平行,且和间的距离为.如果线段在的右侧,并设关于的对称图形是,而关于的对称图形是″″(如图),那么,线段和″″有什么关系?
?
26.
如图,将三角形沿射线方向平移到三角形的位置,连接.
(1)与的位置关系为________;
(2)求证:=;
(3)设=,=,试探索与,之间的数量关系,并证明你的结论.
参考答案
一、
选择题
(本题共计
8
小题
,每题
3
分
,共计24分
)
1.
【答案】
B
【解答】
解:因为等边三角形的外心到三个顶点的距离相等,相邻顶点与外心连线的夹角相等,
所以,,即每次至少旋转.
故选:.
2.
【答案】
D
【解答】
解:如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形;
如果把一个图形绕着某一点旋转,它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称.
,∵
此图形旋转后不能与原图形重合,
∴
此图形不是中心对称图形,是轴对称图形,故此选项错误;
,此图形旋转后能与原图形重合,
∴
此图形是中心对称图形,不是轴对称图形,故此选项错误;
,∵
此图形旋转后不能与原图形重合,
∴
此图形不是中心对称图形,是轴对称图形,故此选项错误;
,∵
此图形旋转后能与原图形重合,
∴
此图形是中心对称图形,且是轴对称图形,故此选项正确.
故选.
3.
【答案】
A
【解答】
解:由题意可知直线是线段的垂直平分线,
∴
.∵
,
∴
,
∴
.
∵
,
∴
,
故选项中的结论错误,选项中的结论正确.
∵
,
∴
,
∴
点为的外心,故选项中的结论正确,
∵
?,,
∴
,故选项中的结论正确.
故选.
4.
【答案】
D
【解答】
、根据中心对称的两个图形全等,即可得到,故正确;
、根据中心对称的两个图形全等,即可得到,故正确;
、根对称点到对称中心的距离相等,即可证得对应线段平行,故正确;
、不正确.
5.
【答案】
D
【解答】
解:∵
对称轴是成轴对称图形中任何一对对应点所连线段的垂直平分线,故本选项错误;
∴
、、错误,正确.
故选.
6.
【答案】
A
【解答】
略
7.
【答案】
D
【解答】
解:根据镜面对称的性质,“”和“”关于镜面对称,“”、“”、“”、“”在镜中的成像还是原数,
则数码“”在正面镜子中的像是,在侧面镜子中的像不是一个位数,
即可得“正面像”和“侧面像”中,只有一个五位数.
故选.
8.
【答案】
D
【解答】
解:如图所示:
过点作于,过点作于,过点作于,
根据旋转的性质可知,,,
∵
四边形是菱形,点,
∴
,,即;
设点坐标为,根据菱形的边长相等可得,
则,解得,
即,
通过旋转图知,此时点落在第二象限,
则点的坐标为.
故选.
二、
填空题
(本题共计
12
小题
,每题
3
分
,共计36分
)
9.
【答案】
【解答】
解:利用作图得垂直平分,
∴
,
∴
的周长
,
∵
四边形为平行四边形,
∴
,,
∴
的周长.
故答案为:.
10.
【答案】
【解答】
解:∵
矩形与矩形关于点成中心对称,
∴
.
故答案为:.
11.
【答案】
一定
【解答】
成轴对称的两个图形一定是全等的.
12.
【答案】
,
【解答】
解:由个图形组成,所以,
故可以看成由一个图形经过次旋转得到的,
每次分别旋转了.
故答案为:,.
13.
【答案】
①②③④
【解答】
解:①矩形既是中心对称图形,又是轴对称图形,正确;
②平行四边形是中心对称图形,不是轴对称图形,正确;
③等腰梯形是轴对称图形,不是中心对称图形,正确;
④有一个锐角是的直角三角形不是中心对称图形,也不是轴对称图形,正确;
综上可得①②③④都正确.
故答案为①②③④.
14.
【答案】
,,
【解答】
解:作图过程:以为圆心任意长为半径作弧,交射线,为,两点,在射线上任取一点(点除外),连接,,
所得,
∵
,是公共边,是角平分线,
∴
全等的依据是.
15.
【答案】
【解答】
解:∵
“北大西洋公约组织”标志的主体部分(平面图)是由四边形绕点进行次旋转变换后形成的,
∴
.
在和中
,
∴
,
∴
,.
即,.
在中,.
故答案为:.
16.
【答案】
【解答】
解:.
∵
,,
∴
.
故答案为:.
17.
【答案】
【解答】
解:将分别与各图形组合能满足组合后是轴对称的有:
,
共种.
故答案为:.
18.
【答案】
【解答】
解:作关于和的对称点,″,连接″,交于,交于,则″即为的周长最小值,作延长线,.
∵
,
∴
,
∴
″,
∵
,″,
∴
,
∴
,
故答案为:.
19.
【答案】
【解答】
解:设马路宽为,
由题意可得出:,,
故.
故答案为:.
20.
【答案】
、,
【解答】
解:如图,连接.过点作于.
“
○在的垂直平分线上,
&
为直角三角形,
故答案为
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
解:如图所示,点即为所求.
如中图所示,点即为所求.
【解答】
解:如图所示,点即为所求.
如中图所示,点即为所求.
22.
【答案】
解:(1)与相等,连接,
∵
点是点关于的对称点,
∴
垂直平分线段,
∴
,
∴
,
即:;
(2),
连接,如图所示,
∵
点是点关于的对称点,
∴
垂直平分线段,
∴
,
∵
,
∴
,
∵
,
∴
.
【解答】
解:(1)与相等,连接,
∵
点是点关于的对称点,
∴
垂直平分线段,
∴
,
∴
,
即:;
(2),
连接,如图所示,
∵
点是点关于的对称点,
∴
垂直平分线段,
∴
,
∵
,
∴
,
∵
,
∴
.
23.
【答案】
解:平移后的图形如下所示:
由题意可知:四边形是等腰梯形,
∴
,,
又是由平移得到的,故,,
∴
..
【解答】
解:平移后的图形如下所示:
由题意可知:四边形是等腰梯形,
∴
,,
又是由平移得到的,故,,
∴
..
24.
【答案】
解:如图所示:
.
【解答】
解:如图所示:
.
25.
【答案】
解:因为平行于,并且″垂直于,当然也垂直于,同理″也垂直于和.
又在平面内垂直于同一条直线的两条直线互相平行,
所以″″.①
另一方面,因为,″,
所以″,
同理″,
所以″″.②
由①②可知,为平行四边形,所以平行且等于.
【解答】
解:因为平行于,并且″垂直于,当然也垂直于,同理″也垂直于和.
又在平面内垂直于同一条直线的两条直线互相平行,
所以″″.①
另一方面,因为,″,
所以″,
同理″,
所以″″.②
由①②可知,为平行四边形,所以平行且等于.
26.
【答案】
根据平移性质可知,,
∴
=,=,
∴
=,
∴
=,
结论:=,
过点作,交于点,
根据平移性质可知,
∴
,
∴
=,=,
∴
===,
即=.
【解答】
由平移的性质可得:;
故答案为:;
根据平移性质可知,,
∴
=,=,
∴
=,
∴
=,
结论:=,
过点作,交于点,
根据平移性质可知,
∴
,
∴
=,=,
∴
===,
即=.
