人教版八年级数学上册教学设计:12、2三角形全等的判定AAS(表格式)
文档属性
| 名称 | 人教版八年级数学上册教学设计:12、2三角形全等的判定AAS(表格式) |
|
|
| 格式 | zip | ||
| 文件大小 | 83.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 00:16:17 | ||
图片预览

文档简介
八年级数学上册教学设计
课题
12、2三角形全等的判定AAS
教学
目标
1.三角形全等的判定三的推论AAS,以及应用AAS判定两个三角形全等
2.三角形全等的判定是证明线段相等、角相等的重要方法
教学
重点
掌握三角形全等的判定AAS,
教学
难点
并会应用它进行线段和角相等的证明
教学
过程
教
学
内
容
与
师
生
活
动
设计意图和
关注的学生
一、两角和其中一角的对边对应相等的两三角形是否全等
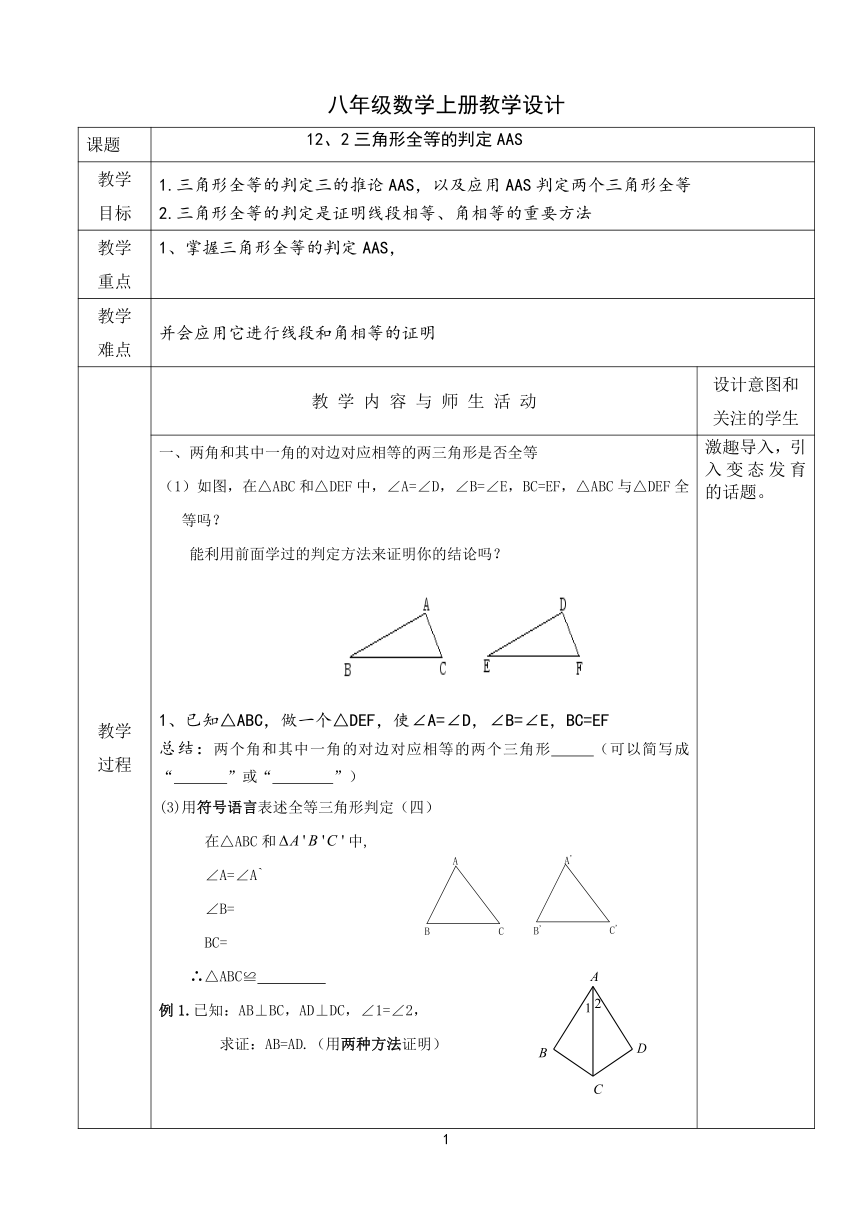
(1)如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF,△ABC与△DEF全等吗?
能利用前面学过的判定方法来证明你的结论吗?
1、已知△ABC,做一个△DEF,使∠A=∠D,∠B=∠E,BC=EF
总结:两个角和其中一角的对边对应相等的两个三角形
(可以简写成“
”或“
”)
(3)用符号语言表述全等三角形判定(四)
在△ABC和中,
∠A=∠A`
∠B=
BC=
∴△ABC≌
例1.已知:AB⊥BC,AD⊥DC,∠1=∠2,
求证:AB=AD.(用两种方法证明)
课堂练习
1、如图,已知∠B=∠DEF,AB=DE,请添加一个条件使
△ABC≌△DEF,则需添加的条件是__________(只需写出一个).
2、如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是(
)
A.带①去
B.带②去
C.带③去
D.带②和③去
3、.如图所示,已知∠A=∠D,∠1=∠2,那么要
得到△ABC≌△DEF,还应给出的条件是:(
)
A.
∠B=∠E
B.ED=BC
C.
AB=EF
D.AF=CD
4、如图,∠DAC=∠BCA,∠B=∠D
求证:AB=CD
5、已知:AE∥CF,且AE=CF,AB⊥EF于B,CD⊥EF于D.
求证:(1)BE=DF
(2)
FB=DE.
6、已知:如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B
求证:△ABC≌△CDE
激趣导入,引入变态发育的话题。
板
书
设
计
三角形全等的判定AAS
教
学
反
思
1
课题
12、2三角形全等的判定AAS
教学
目标
1.三角形全等的判定三的推论AAS,以及应用AAS判定两个三角形全等
2.三角形全等的判定是证明线段相等、角相等的重要方法
教学
重点
掌握三角形全等的判定AAS,
教学
难点
并会应用它进行线段和角相等的证明
教学
过程
教
学
内
容
与
师
生
活
动
设计意图和
关注的学生
一、两角和其中一角的对边对应相等的两三角形是否全等
(1)如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF,△ABC与△DEF全等吗?
能利用前面学过的判定方法来证明你的结论吗?
1、已知△ABC,做一个△DEF,使∠A=∠D,∠B=∠E,BC=EF
总结:两个角和其中一角的对边对应相等的两个三角形
(可以简写成“
”或“
”)
(3)用符号语言表述全等三角形判定(四)
在△ABC和中,
∠A=∠A`
∠B=
BC=
∴△ABC≌
例1.已知:AB⊥BC,AD⊥DC,∠1=∠2,
求证:AB=AD.(用两种方法证明)
课堂练习
1、如图,已知∠B=∠DEF,AB=DE,请添加一个条件使
△ABC≌△DEF,则需添加的条件是__________(只需写出一个).
2、如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是(
)
A.带①去
B.带②去
C.带③去
D.带②和③去
3、.如图所示,已知∠A=∠D,∠1=∠2,那么要
得到△ABC≌△DEF,还应给出的条件是:(
)
A.
∠B=∠E
B.ED=BC
C.
AB=EF
D.AF=CD
4、如图,∠DAC=∠BCA,∠B=∠D
求证:AB=CD
5、已知:AE∥CF,且AE=CF,AB⊥EF于B,CD⊥EF于D.
求证:(1)BE=DF
(2)
FB=DE.
6、已知:如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B
求证:△ABC≌△CDE
激趣导入,引入变态发育的话题。
板
书
设
计
三角形全等的判定AAS
教
学
反
思
1
