人教版八年级数学上册教学设计:13.3.2 等边三角形(1)(表格式)
文档属性
| 名称 | 人教版八年级数学上册教学设计:13.3.2 等边三角形(1)(表格式) |

|
|
| 格式 | zip | ||
| 文件大小 | 138.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 00:23:29 | ||
图片预览

文档简介
八年级数学上册教学设计
课题
13.3.2
等边三角形(1)
教学
目标
1.等边三角形的性质和判定方法。
2.用等边三角形的性质和判定解题
3.会利用等边三角形的性质、判定进行计算和证明。
4.等边三角形是等腰三角形的特殊情形
教学
重点
等腰三角形与等边三角形性质的区别联系。
教学
难点
等边三角形的性质和判定方法,
教学
过程
教
学
内
容
与
师
生
活
动
设计意图和
关注的学生
复习引入:
1.什么是等腰三角形,什么是等边三角形?
2.等边三角形与等腰三角形的关系
新授课:
1.等边三角形有什么性质?
对比等腰三角形的性质,写出等边三角形的性质
教师总结:
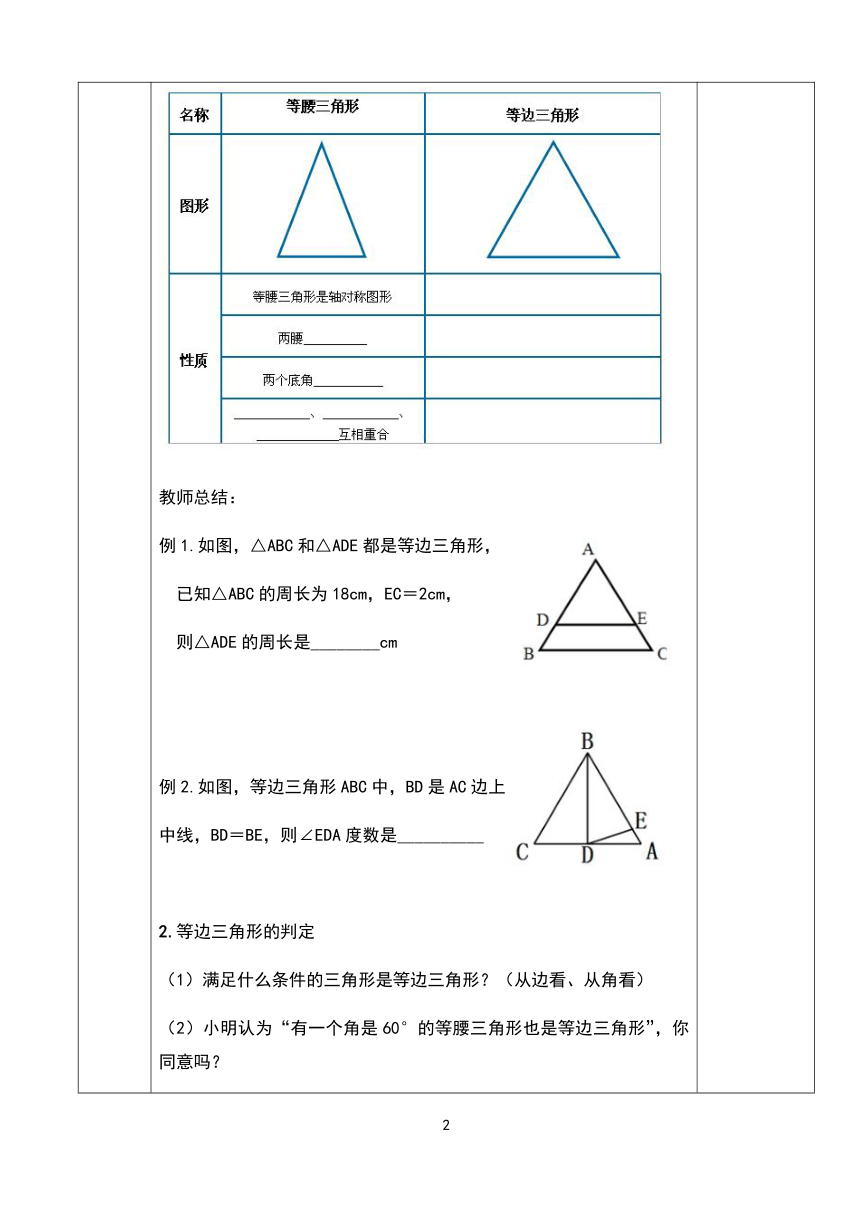
例1.如图,△ABC和△ADE都是等边三角形,
已知△ABC的周长为18cm,EC=2cm,
则△ADE的周长是________cm
例2.如图,等边三角形ABC中,BD是AC边上的
中线,BD=BE,则∠EDA度数是__________
2.等边三角形的判定
(1)满足什么条件的三角形是等边三角形?(从边看、从角看)
(2)小明认为“有一个角是60°的等腰三角形也是等边三角形”,你同意吗?
例3.如图,在等边三角形ABC中,DE∥BC,请问△ADE是等边三角形吗?说明理由?
分析:此题可有至少两种方法:
(1)有一角等于60°的等腰三角形是等边三角形。
(2)三个角都是60°的三角形是等边三角形。
上题中,若将条件DE∥BC改为AD=AE,△ADE还是等边三角形吗?说明理由
分析:
课堂练习
1.
等边三角形两条角平分线所夹的锐角的度数是(
)
A.30°
B.45°
C.
60°
D.
90°
2.
下面给出的几种三角形:
①有两个角为60°的三角形;②三个外角都相等的三角形
③一边上的高也是这边上的中线的三角形;
④有一个角为60°的等腰三角形。
其中是等边三角形的个数是
(
)
A.
4个
B.
3个
C.
2个
D.
1个
3.
三角形的三边长可以是(
).
A.
2,11,13
B.5,12,7
C.5,5,11 D.6,12,13
4.如图,在△ABC中,
BD是的AC边上的高,∠A=55°,求:∠ABD的大小
5.已知:如图,
△ABD和△ACE均为等边三角形,
求证:△ADC≌△ABE
6.已知:如图,C是线段AB上的一点,
分别以AC和BC为边,
在线段AB的同侧作等边△ACM和△CBN.
求证:AN=MB
板
书
设
计
1.等边三角形的性质:
2.等边三角形的判定方法:
教
学
反
思
1
课题
13.3.2
等边三角形(1)
教学
目标
1.等边三角形的性质和判定方法。
2.用等边三角形的性质和判定解题
3.会利用等边三角形的性质、判定进行计算和证明。
4.等边三角形是等腰三角形的特殊情形
教学
重点
等腰三角形与等边三角形性质的区别联系。
教学
难点
等边三角形的性质和判定方法,
教学
过程
教
学
内
容
与
师
生
活
动
设计意图和
关注的学生
复习引入:
1.什么是等腰三角形,什么是等边三角形?
2.等边三角形与等腰三角形的关系
新授课:
1.等边三角形有什么性质?
对比等腰三角形的性质,写出等边三角形的性质
教师总结:
例1.如图,△ABC和△ADE都是等边三角形,
已知△ABC的周长为18cm,EC=2cm,
则△ADE的周长是________cm
例2.如图,等边三角形ABC中,BD是AC边上的
中线,BD=BE,则∠EDA度数是__________
2.等边三角形的判定
(1)满足什么条件的三角形是等边三角形?(从边看、从角看)
(2)小明认为“有一个角是60°的等腰三角形也是等边三角形”,你同意吗?
例3.如图,在等边三角形ABC中,DE∥BC,请问△ADE是等边三角形吗?说明理由?
分析:此题可有至少两种方法:
(1)有一角等于60°的等腰三角形是等边三角形。
(2)三个角都是60°的三角形是等边三角形。
上题中,若将条件DE∥BC改为AD=AE,△ADE还是等边三角形吗?说明理由
分析:
课堂练习
1.
等边三角形两条角平分线所夹的锐角的度数是(
)
A.30°
B.45°
C.
60°
D.
90°
2.
下面给出的几种三角形:
①有两个角为60°的三角形;②三个外角都相等的三角形
③一边上的高也是这边上的中线的三角形;
④有一个角为60°的等腰三角形。
其中是等边三角形的个数是
(
)
A.
4个
B.
3个
C.
2个
D.
1个
3.
三角形的三边长可以是(
).
A.
2,11,13
B.5,12,7
C.5,5,11 D.6,12,13
4.如图,在△ABC中,
BD是的AC边上的高,∠A=55°,求:∠ABD的大小
5.已知:如图,
△ABD和△ACE均为等边三角形,
求证:△ADC≌△ABE
6.已知:如图,C是线段AB上的一点,
分别以AC和BC为边,
在线段AB的同侧作等边△ACM和△CBN.
求证:AN=MB
板
书
设
计
1.等边三角形的性质:
2.等边三角形的判定方法:
教
学
反
思
1
