人教版九年级下册数学 29.1 投影 同步测试(Word版 含解析)
文档属性
| 名称 | 人教版九年级下册数学 29.1 投影 同步测试(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 135.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 00:00:00 | ||
图片预览



文档简介
29.1
投影
同步测试
一.选择题
1.在同一时刻,两根长度不等的竿子置于阳光之下,但看到它们的影长相等,那么这两根竿子的相对位置是( )
A.两竿都垂直于地面
B.两竿平行斜插在地上
C.两根竿子不平行
D.两根都倒在地面上
2.如图,在直角坐标系中,点P(2,2)是一个光源.木杆AB两端的坐标分别为(0,1),(3,1).则木杆AB在x轴上的投影长为( )
A.3
B.5
C.6
D.7
3.木棒长为1.5m,则它的正投影的长一定( )
A.大于1.5m
B.小于1.5m
C.等于1.5m
D.小于或等于1.5m
4.小阳和小明两人从远处沿直线走到路灯下,他们规定:小阳在前,小明在后,两人之间的距离始终与小阳的影长相等.在这种情况下,他们两人之间的距离( )
A.始终不变
B.越来越远
C.时近时远
D.越来越近
5.下图是某学校操场上单杠(图中实线部分)在地面上的影子(图中虚线部分),根据图中所示,可判断形成该影子的光线为( )
A.太阳光线
B.灯光光线
C.可能为太阳光线或灯光光线
D.该影子实际不可能存在
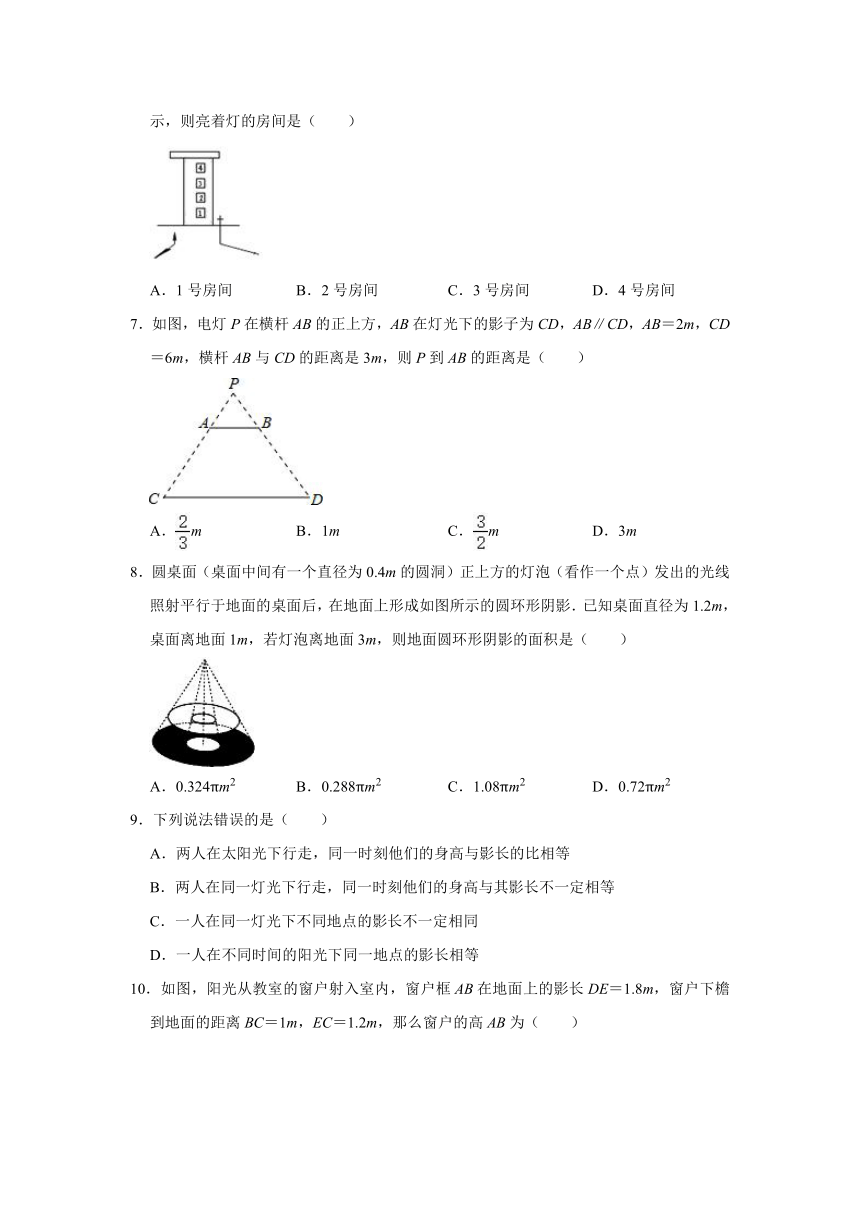
6.一幢4层楼房只有一个房间亮着灯,一棵小树和一根电线杆在窗口灯光下的影子如图所示,则亮着灯的房间是( )
A.1号房间
B.2号房间
C.3号房间
D.4号房间
7.如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=6m,横杆AB与CD的距离是3m,则P到AB的距离是( )
A.m
B.1m
C.m
D.3m
8.圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )
A.0.324πm2
B.0.288πm2
C.1.08πm2
D.0.72πm2
9.下列说法错误的是( )
A.两人在太阳光下行走,同一时刻他们的身高与影长的比相等
B.两人在同一灯光下行走,同一时刻他们的身高与其影长不一定相等
C.一人在同一灯光下不同地点的影长不一定相同
D.一人在不同时间的阳光下同一地点的影长相等
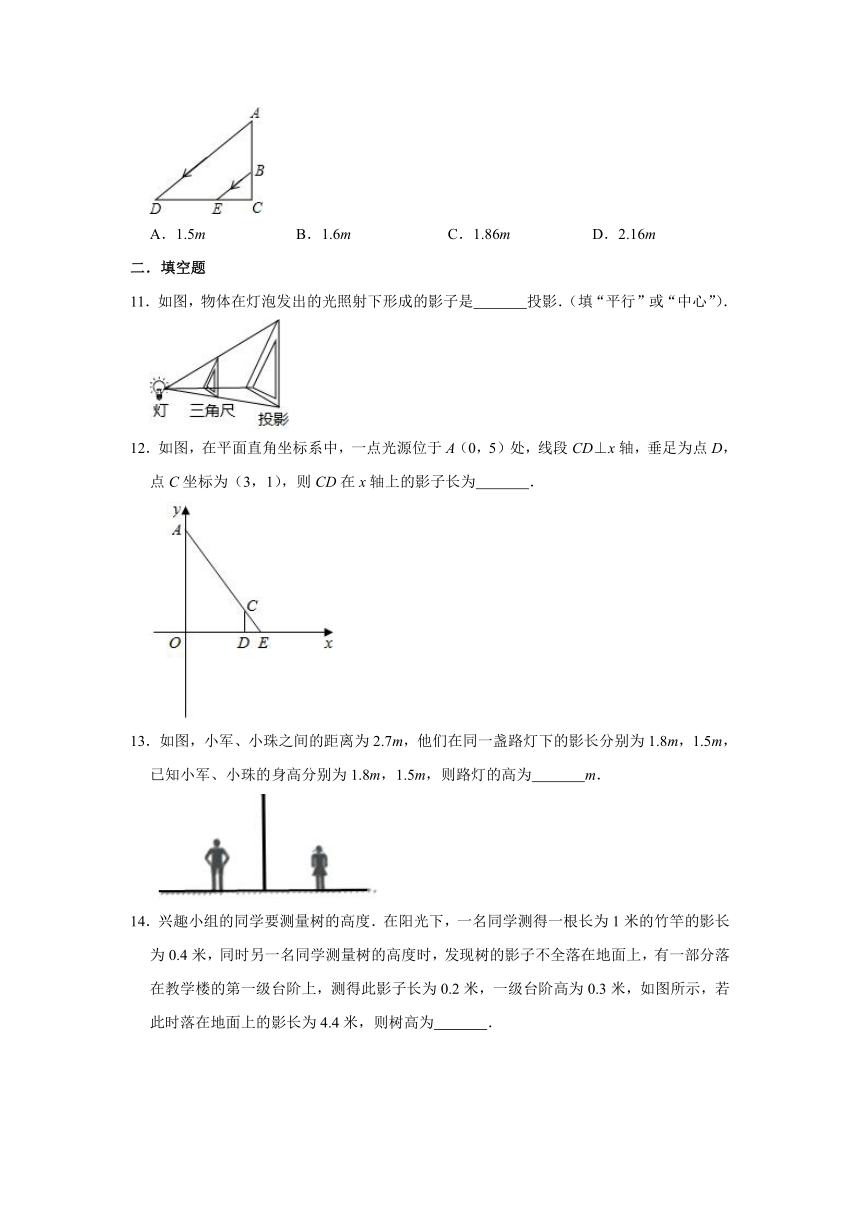
10.如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8m,窗户下檐到地面的距离BC=1m,EC=1.2m,那么窗户的高AB为( )
A.1.5m
B.1.6m
C.1.86m
D.2.16m
二.填空题
11.如图,物体在灯泡发出的光照射下形成的影子是
投影.(填“平行”或“中心”).
12.如图,在平面直角坐标系中,一点光源位于A(0,5)处,线段CD⊥x轴,垂足为点D,点C坐标为(3,1),则CD在x轴上的影子长为
.
13.如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,则路灯的高为
m.
14.兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为1米的竹竿的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米,则树高为
.
15.如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在图的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,则小桥所在圆的半径
.
三.解答题
16.如图,在路灯的同侧有两根高度相同的木棒,请分别画出这两根木棒的影子.
17.已知如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=2m.
(1)请你画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为4m,请你计算DE的长.
18.如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=14.5米,NF=0.2米.设太阳光线与水平地面的夹角为α,当α=56.3°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的NF这层上晒太阳.
(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.(参考数据:sin56.3°≈0.83,cos56.3°≈0.55,tan56.3°≈1.5)
参考答案
一.选择题
1.解:因为在同一时刻,两根长度不等的竿子置于阳光之下,但看到它们的影长相等
所以这两根竿子肯定不平行.
故选:C.
2.解:延长PA、PB分别交x轴于A′、B′,作PE⊥x轴于E,交AB于D,如图,
∵P(2,2),A(0,1),B(3,1).
∴PD=1,PE=2,AB=3,
∵AB∥A′B′,
∴△PAB∽△PA′B′,
∴=,即=,
∴A′B′=6,
故选:C.
3.解:正投影的长度与木棒的摆放角度有关系,但无论怎样摆都不会超过1.5
m.
故选:D.
4.解:因为小阳和小明两人从远处沿直线走到路灯下这一过程中离光源是由远到近的过程,所以他在地上的影子会变短,所以他们两人之间的距离越来越近.故选D.
5.解:若形成的影子是由太阳光照射形成的影子,则两直线一定平行;若形成的影子是由灯光照射而形成的影子,则两直线一定相交.所以可判断形成该影子的光线为灯光光线.故选B.
6.解:如图所示,
故选:B.
7.解:∵AB∥CD,
∴△PAB∽△PCD,
∴AB:CD=P到AB的距离:点P到CD的距离.
∴2:6=P到AB的距离:3+P到AB的距离,
∴P到AB的距离为m.
故选:C.
8.解:如图所示:∵AC⊥OB,BD⊥OB,
∴△AOC∽△BOD,
∴=,即=,
解得:BD=0.9m,
同理可得:AC′=0.2m,则BD′=0.3m,
∴S圆环形阴影=0.92
π﹣0.32π=0.72π(m2).
故选:D.
9.解:A、两人在太阳光下行走,同一时刻他们的身高与影长的比相等,正确,不合题意;
B、两人在同一灯光下行走,同一时刻他们的身高与其影长不一定相等,正确,不合题意;
C、一人在同一灯光下不同地点的影长不一定相同,正确,不合题意;
D、一人在不同时间的阳光下同一地点的影长相等,错误,符合题意.
故选:D.
10.解:∵BE∥AD,
∴△BCE∽△ACD,
∴即=
且BC=1,DE=1.8,EC=1.2
∴=
∴1.2AB=1.8,
∴AB=1.5m.
故选:A.
二.填空题
11.解:由于光源是由一点发出的,因此是中心投影,
故答案为:中心.
12.解:∵DC∥AO,
∴△ECD∽△EAO,
∴=,
∴=,
解得DE=,
即CD在x轴上的影子长为:;
故答案为:.
13.解:如图,∵CD∥AB∥MN,
∴△ABE∽△CDE,△ABF∽△MNF,
∴,,
即,,
解得:AB=3m.
答:路灯的高为3m.
14.解:根据题意可构造相似三角形模型如图,
其中AB为树高,EF为树影在第一级台阶上的影长,BD为树影在地上部分的长,ED的长为台阶高,并且由光沿直线传播的性质可知BC即为树影在地上的全长;
延长FE交AB于G,则Rt△ABC∽Rt△AGF,
∴AG:GF=AB:BC=物高:影长=1:0.4
∴GF=0.4AG
又∵GF=GE+EF,BD=GE,GE=4.4m,EF=0.2m,
∴GF=4.6
∴AG=11.5
∴AB=AG+GB=11.8,即树高为11.8米.
15.解:小桥所在圆的圆心为点O,连结OG,设⊙O的半径为Rm,如图,
∵=,
∴=,解得GH=8,
∵MN为弧GH的中点到弦GH的距离,
∴点O在直线MN上,GM=HM=GH=4,
在Rt△OGM中,OM=R﹣2,OG=R,GM=4,
∵OM2+GM2=OG2,
∴(R﹣2)2+42=R2,解得R=5,
即⊙O的半径为5m.
故答案为为5m.
三.解答题
16.解:如图所示:
17.解:(1)如图,EF为此时DE在阳光下的投影;
(2)∵AC∥DF,
∴∠ACB=∠DFE,
∴Rt△ABC∽Rt△DEF,
∴=,即=,解得DE=10(m),
即DE的长为10m.
18.解:(1)当α=56.3°时,在Rt△ABE中,
∵tan56.3°=≈1.50,
∴AB=10?tan56.3°≈10×1.50=15(m),
即楼房的高度约为15米;
(2)当α=45°时,小猫不能再晒到太阳,
理由如下:假设没有台阶,当α=45°时,从点B射下的光线与地面AD交于点P,此时的影长AP=AB≈15m,
设MN的延长线交AD于点H,
∵AC=14.5m,NF=0.2m,
∴PH=AP﹣AC﹣CH≈15﹣14.5﹣0.2=0.3(m),
设直线MN与BP交于点Q,则HQ=PH=0.3m,
∴点Q在MN上,
∴大楼的影子落在MN这个侧面上,
∴小猫不能晒到太阳.
投影
同步测试
一.选择题
1.在同一时刻,两根长度不等的竿子置于阳光之下,但看到它们的影长相等,那么这两根竿子的相对位置是( )
A.两竿都垂直于地面
B.两竿平行斜插在地上
C.两根竿子不平行
D.两根都倒在地面上
2.如图,在直角坐标系中,点P(2,2)是一个光源.木杆AB两端的坐标分别为(0,1),(3,1).则木杆AB在x轴上的投影长为( )
A.3
B.5
C.6
D.7
3.木棒长为1.5m,则它的正投影的长一定( )
A.大于1.5m
B.小于1.5m
C.等于1.5m
D.小于或等于1.5m
4.小阳和小明两人从远处沿直线走到路灯下,他们规定:小阳在前,小明在后,两人之间的距离始终与小阳的影长相等.在这种情况下,他们两人之间的距离( )
A.始终不变
B.越来越远
C.时近时远
D.越来越近
5.下图是某学校操场上单杠(图中实线部分)在地面上的影子(图中虚线部分),根据图中所示,可判断形成该影子的光线为( )
A.太阳光线
B.灯光光线
C.可能为太阳光线或灯光光线
D.该影子实际不可能存在
6.一幢4层楼房只有一个房间亮着灯,一棵小树和一根电线杆在窗口灯光下的影子如图所示,则亮着灯的房间是( )
A.1号房间
B.2号房间
C.3号房间
D.4号房间
7.如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=6m,横杆AB与CD的距离是3m,则P到AB的距离是( )
A.m
B.1m
C.m
D.3m
8.圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )
A.0.324πm2
B.0.288πm2
C.1.08πm2
D.0.72πm2
9.下列说法错误的是( )
A.两人在太阳光下行走,同一时刻他们的身高与影长的比相等
B.两人在同一灯光下行走,同一时刻他们的身高与其影长不一定相等
C.一人在同一灯光下不同地点的影长不一定相同
D.一人在不同时间的阳光下同一地点的影长相等
10.如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8m,窗户下檐到地面的距离BC=1m,EC=1.2m,那么窗户的高AB为( )
A.1.5m
B.1.6m
C.1.86m
D.2.16m
二.填空题
11.如图,物体在灯泡发出的光照射下形成的影子是
投影.(填“平行”或“中心”).
12.如图,在平面直角坐标系中,一点光源位于A(0,5)处,线段CD⊥x轴,垂足为点D,点C坐标为(3,1),则CD在x轴上的影子长为
.
13.如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,则路灯的高为
m.
14.兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为1米的竹竿的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米,则树高为
.
15.如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在图的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,则小桥所在圆的半径
.
三.解答题
16.如图,在路灯的同侧有两根高度相同的木棒,请分别画出这两根木棒的影子.
17.已知如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=2m.
(1)请你画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为4m,请你计算DE的长.
18.如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=14.5米,NF=0.2米.设太阳光线与水平地面的夹角为α,当α=56.3°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的NF这层上晒太阳.
(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.(参考数据:sin56.3°≈0.83,cos56.3°≈0.55,tan56.3°≈1.5)
参考答案
一.选择题
1.解:因为在同一时刻,两根长度不等的竿子置于阳光之下,但看到它们的影长相等
所以这两根竿子肯定不平行.
故选:C.
2.解:延长PA、PB分别交x轴于A′、B′,作PE⊥x轴于E,交AB于D,如图,
∵P(2,2),A(0,1),B(3,1).
∴PD=1,PE=2,AB=3,
∵AB∥A′B′,
∴△PAB∽△PA′B′,
∴=,即=,
∴A′B′=6,
故选:C.
3.解:正投影的长度与木棒的摆放角度有关系,但无论怎样摆都不会超过1.5
m.
故选:D.
4.解:因为小阳和小明两人从远处沿直线走到路灯下这一过程中离光源是由远到近的过程,所以他在地上的影子会变短,所以他们两人之间的距离越来越近.故选D.
5.解:若形成的影子是由太阳光照射形成的影子,则两直线一定平行;若形成的影子是由灯光照射而形成的影子,则两直线一定相交.所以可判断形成该影子的光线为灯光光线.故选B.
6.解:如图所示,
故选:B.
7.解:∵AB∥CD,
∴△PAB∽△PCD,
∴AB:CD=P到AB的距离:点P到CD的距离.
∴2:6=P到AB的距离:3+P到AB的距离,
∴P到AB的距离为m.
故选:C.
8.解:如图所示:∵AC⊥OB,BD⊥OB,
∴△AOC∽△BOD,
∴=,即=,
解得:BD=0.9m,
同理可得:AC′=0.2m,则BD′=0.3m,
∴S圆环形阴影=0.92
π﹣0.32π=0.72π(m2).
故选:D.
9.解:A、两人在太阳光下行走,同一时刻他们的身高与影长的比相等,正确,不合题意;
B、两人在同一灯光下行走,同一时刻他们的身高与其影长不一定相等,正确,不合题意;
C、一人在同一灯光下不同地点的影长不一定相同,正确,不合题意;
D、一人在不同时间的阳光下同一地点的影长相等,错误,符合题意.
故选:D.
10.解:∵BE∥AD,
∴△BCE∽△ACD,
∴即=
且BC=1,DE=1.8,EC=1.2
∴=
∴1.2AB=1.8,
∴AB=1.5m.
故选:A.
二.填空题
11.解:由于光源是由一点发出的,因此是中心投影,
故答案为:中心.
12.解:∵DC∥AO,
∴△ECD∽△EAO,
∴=,
∴=,
解得DE=,
即CD在x轴上的影子长为:;
故答案为:.
13.解:如图,∵CD∥AB∥MN,
∴△ABE∽△CDE,△ABF∽△MNF,
∴,,
即,,
解得:AB=3m.
答:路灯的高为3m.
14.解:根据题意可构造相似三角形模型如图,
其中AB为树高,EF为树影在第一级台阶上的影长,BD为树影在地上部分的长,ED的长为台阶高,并且由光沿直线传播的性质可知BC即为树影在地上的全长;
延长FE交AB于G,则Rt△ABC∽Rt△AGF,
∴AG:GF=AB:BC=物高:影长=1:0.4
∴GF=0.4AG
又∵GF=GE+EF,BD=GE,GE=4.4m,EF=0.2m,
∴GF=4.6
∴AG=11.5
∴AB=AG+GB=11.8,即树高为11.8米.
15.解:小桥所在圆的圆心为点O,连结OG,设⊙O的半径为Rm,如图,
∵=,
∴=,解得GH=8,
∵MN为弧GH的中点到弦GH的距离,
∴点O在直线MN上,GM=HM=GH=4,
在Rt△OGM中,OM=R﹣2,OG=R,GM=4,
∵OM2+GM2=OG2,
∴(R﹣2)2+42=R2,解得R=5,
即⊙O的半径为5m.
故答案为为5m.
三.解答题
16.解:如图所示:
17.解:(1)如图,EF为此时DE在阳光下的投影;
(2)∵AC∥DF,
∴∠ACB=∠DFE,
∴Rt△ABC∽Rt△DEF,
∴=,即=,解得DE=10(m),
即DE的长为10m.
18.解:(1)当α=56.3°时,在Rt△ABE中,
∵tan56.3°=≈1.50,
∴AB=10?tan56.3°≈10×1.50=15(m),
即楼房的高度约为15米;
(2)当α=45°时,小猫不能再晒到太阳,
理由如下:假设没有台阶,当α=45°时,从点B射下的光线与地面AD交于点P,此时的影长AP=AB≈15m,
设MN的延长线交AD于点H,
∵AC=14.5m,NF=0.2m,
∴PH=AP﹣AC﹣CH≈15﹣14.5﹣0.2=0.3(m),
设直线MN与BP交于点Q,则HQ=PH=0.3m,
∴点Q在MN上,
∴大楼的影子落在MN这个侧面上,
∴小猫不能晒到太阳.
