人教版七年级数学上册同步检测:4.3.2 角的比较与运算(word版,含答案)
文档属性
| 名称 | 人教版七年级数学上册同步检测:4.3.2 角的比较与运算(word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 408.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 00:00:00 | ||
图片预览


文档简介
4.3.2
角的比较与运算
一、选择题(共7小题;共35分)
1.
下列关于角平分线的说法中,正确的是
A.
平分角的一条线段
B.
平分一个角的一条直线
C.
以一个角的顶点为端点且把这个角分成相等的两个角的一条线段
D.
以—个角的顶点为端点且把这个角分成相等的两个角的一条射线
2.
如图所示,若有
,,则下列结论中错误的是
A.
是
的平分线
B.
是
的平分线
C.
D.
是
的平分线
3.
如图所示,若
,那么
A.
B.
C.
D.
与
的大小不能确定
4.
比较
与
时,把它们的顶点
和边
重合,把
和
放在
的同一侧,若
,则
A.
落在
的内部
B.
落在
的外部
C.
和
重合
D.
不能确定
的位置
5.
在
的内部任取一点
,作射线
,那么有
A.
B.
C.
D.
6.
借助一副三角尺,你能画出下面哪个度数的角
A.
B.
C.
D.
7.
如图所示,将一副三角板叠放在一起,使直角的顶点重合于点
,则
的值
A.
小于
或等于
B.
等于
C.
大于
D.
大于
或等于
二、填空题(共4小题;共20分)
8.
已知
,
是
的平分线,则
?度.
9.
如图,若
,,则
?;
若
,,,则
?,
?,
?.
10.
如图,
是
的平分线,
比
大
,
的度数
?.
11.
如图所示,
是直线
上一点,,
平分
,则
?.
三、解答题(共8小题;共96分)
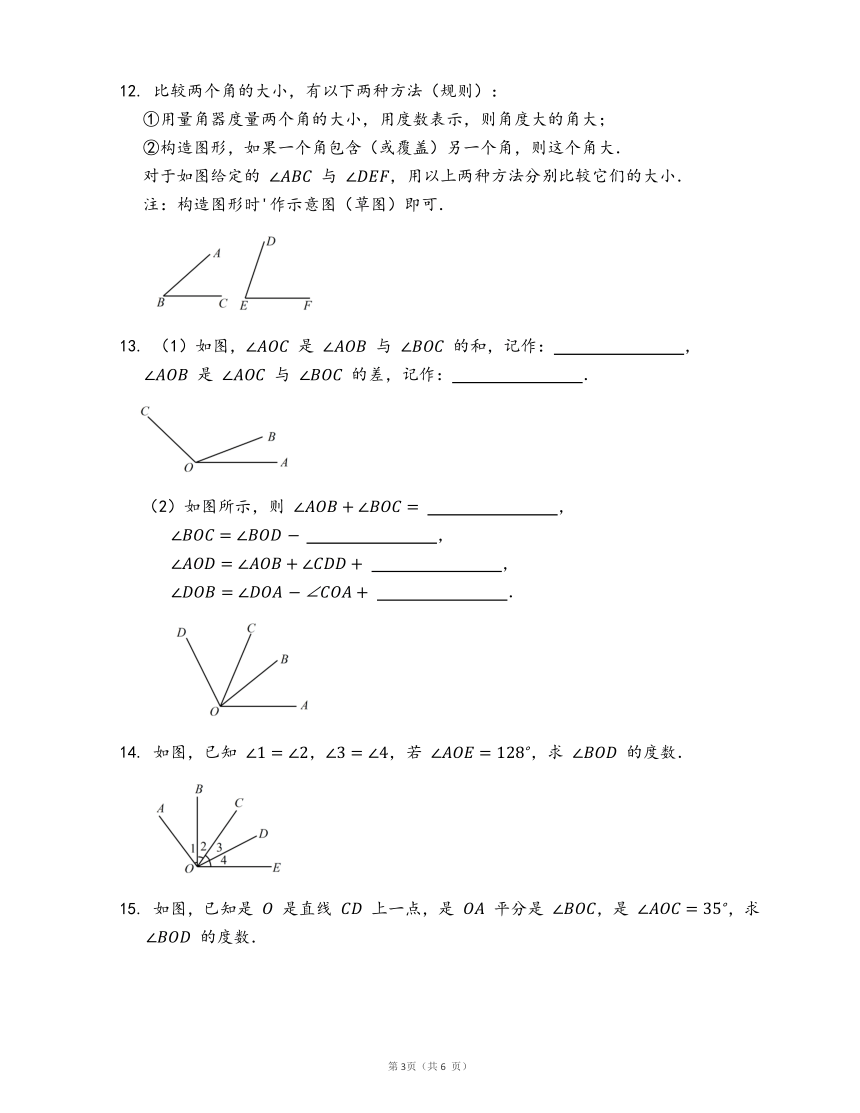
12.
比较两个角的大小,有以下两种方法(规则):
①用量角器度量两个角的大小,用度数表示,则角度大的角大;
②构造图形,如果一个角包含(或覆盖)另一个角,则这个角大.
对于如图给定的
与
,用以上两种方法分别比较它们的大小.
注:构造图形时'作示意图(草图)即可.
13.
(1)如图,
是
与
的和,记作:
?,
是
与
的差,记作:
?.
(2)如图所示,则
?,
?,
?,
?.
14.
如图,已知
,,若
,求
的度数.
15.
如图,已知是
是直线
上一点,是
平分是
,是
,求
的度数.
16.
计算:
(1);
(2).
17.
如图,
是直线
上一点,
平分
,
平分
.
(1)你能求出
的度数吗?你能得出什么结论?
(2)如果
,求
的度数.
18.
已知
,,
平分
,
平分
,求
的度数.
19.
如图,
是直角,,
是
的平分线,
是
的平分线.
(1)求
的大小;
(2)当锐角
的大小发生改变时,
的大小也会发生改变吗?为什么?
答案
第一部分
1.
D
2.
D
3.
B
4.
A
5.
D
6.
B
7.
B
第二部分
8.
【解析】,
是
的平分线,
.
9.
,,,
10.
11.
第三部分
12.
13.
(1)
;
??????(2)
;;;
14.
15.
的度数为
.
16.
(1)
??????(2)
17.
(1)
由角平分线的定义可知
,.
再由图中角的关系得
,
所以
.
结论:
的度数恒为
,和射线
的位置无关.
??????(2)
.
18.
分两种情况讨论:
①若
与
在边
的同侧,如图①所示.
因为
平分
,
所以
.
又因为
平分
,
所以
.
所以有
.
②若
与
在边
的两侧,如图②所示.
此时,因为
平分
,
所以
.
又因为
平分
,
所以
.
所以
.
所以
的度数为
或
.
19.
(1)
因为
是直角,,
所以
.
因为
是
的平分线,
是
的平分线,
所以
,
,
所以
.
??????(2)
不会发生变化,
的大小与
无关,总是等于
的—半.
第5页(共6
页)
角的比较与运算
一、选择题(共7小题;共35分)
1.
下列关于角平分线的说法中,正确的是
A.
平分角的一条线段
B.
平分一个角的一条直线
C.
以一个角的顶点为端点且把这个角分成相等的两个角的一条线段
D.
以—个角的顶点为端点且把这个角分成相等的两个角的一条射线
2.
如图所示,若有
,,则下列结论中错误的是
A.
是
的平分线
B.
是
的平分线
C.
D.
是
的平分线
3.
如图所示,若
,那么
A.
B.
C.
D.
与
的大小不能确定
4.
比较
与
时,把它们的顶点
和边
重合,把
和
放在
的同一侧,若
,则
A.
落在
的内部
B.
落在
的外部
C.
和
重合
D.
不能确定
的位置
5.
在
的内部任取一点
,作射线
,那么有
A.
B.
C.
D.
6.
借助一副三角尺,你能画出下面哪个度数的角
A.
B.
C.
D.
7.
如图所示,将一副三角板叠放在一起,使直角的顶点重合于点
,则
的值
A.
小于
或等于
B.
等于
C.
大于
D.
大于
或等于
二、填空题(共4小题;共20分)
8.
已知
,
是
的平分线,则
?度.
9.
如图,若
,,则
?;
若
,,,则
?,
?,
?.
10.
如图,
是
的平分线,
比
大
,
的度数
?.
11.
如图所示,
是直线
上一点,,
平分
,则
?.
三、解答题(共8小题;共96分)
12.
比较两个角的大小,有以下两种方法(规则):
①用量角器度量两个角的大小,用度数表示,则角度大的角大;
②构造图形,如果一个角包含(或覆盖)另一个角,则这个角大.
对于如图给定的
与
,用以上两种方法分别比较它们的大小.
注:构造图形时'作示意图(草图)即可.
13.
(1)如图,
是
与
的和,记作:
?,
是
与
的差,记作:
?.
(2)如图所示,则
?,
?,
?,
?.
14.
如图,已知
,,若
,求
的度数.
15.
如图,已知是
是直线
上一点,是
平分是
,是
,求
的度数.
16.
计算:
(1);
(2).
17.
如图,
是直线
上一点,
平分
,
平分
.
(1)你能求出
的度数吗?你能得出什么结论?
(2)如果
,求
的度数.
18.
已知
,,
平分
,
平分
,求
的度数.
19.
如图,
是直角,,
是
的平分线,
是
的平分线.
(1)求
的大小;
(2)当锐角
的大小发生改变时,
的大小也会发生改变吗?为什么?
答案
第一部分
1.
D
2.
D
3.
B
4.
A
5.
D
6.
B
7.
B
第二部分
8.
【解析】,
是
的平分线,
.
9.
,,,
10.
11.
第三部分
12.
13.
(1)
;
??????(2)
;;;
14.
15.
的度数为
.
16.
(1)
??????(2)
17.
(1)
由角平分线的定义可知
,.
再由图中角的关系得
,
所以
.
结论:
的度数恒为
,和射线
的位置无关.
??????(2)
.
18.
分两种情况讨论:
①若
与
在边
的同侧,如图①所示.
因为
平分
,
所以
.
又因为
平分
,
所以
.
所以有
.
②若
与
在边
的两侧,如图②所示.
此时,因为
平分
,
所以
.
又因为
平分
,
所以
.
所以
.
所以
的度数为
或
.
19.
(1)
因为
是直角,,
所以
.
因为
是
的平分线,
是
的平分线,
所以
,
,
所以
.
??????(2)
不会发生变化,
的大小与
无关,总是等于
的—半.
第5页(共6
页)
