2019-2020学年北京市通州区北京版六年级下册期末综合测试数学试卷(含答案解析)
文档属性
| 名称 | 2019-2020学年北京市通州区北京版六年级下册期末综合测试数学试卷(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 320.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 09:50:35 | ||
图片预览




文档简介
2019-2020学年北京市通州区北京版六年级下册期末综合测试数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.台湾是我国领土不可分割的一部分。台湾岛的面积约为三万六千一百九十一平方千米,写作(______)平方千米,省略“万”后面的位数约是(______)万平方千米。
2.一个数既是6的因数,又是6的倍数,这个数是(________________).
3.b=15a,当a=0.6时,b=(______)。
4.在比例中,两个内项的积是12,一个外项是,另一个外项是(________)。
5.一个三角形的两个内角分别是65°和25°,另一个内角是(______)度。这个三角形是(______)三角形。
6.做一个长8厘米,宽6厘米,高5厘米的长方体框架需要铁丝____厘米。
7.一个圆柱和一个圆锥的底面积相等,圆锥的高是圆柱高的3倍,圆锥的体积是12立方分米,圆柱的体积是(______)立方分米。
8.把2个面包平均分给2个小朋友,每个小朋友分到这些面包的,每人分得( )个面包。
9.10以内所有的质数的和是_____.
二、作图题
10.把﹣0.5、、2在直线上表示出来。
11.在下面的方格图中画一个与三角形面积相等的梯形。
三、选择题
12.三个连续自然数的平均数是8,这三个连续自然数分别是( )。
A.6、7、8 B.7、8、9 C.8、9、10
13.下面分数能化成有限小数的是( )。
A. B. C.
14.甲、乙两数都是非0自然数,如果甲数是乙数的倍数,那么甲数和乙数的最小公倍数是( )。
A.乙数 B.甲数 C.甲、乙两数的乘积
15.过直线外一点能画( )已知直线的垂线
A.无数条 B.两条 C.一条
16.某工厂女工人数与男工人数比是3∶5,女工人数是全厂工人总数的( )。
A.37.5% B.60% C.62.5%
17.下面三个立体图形从( )面看到的形状完全一样。
A.上面 B.前面 C.左面
18.豆芽的发芽率一定,发芽豆子的颗数与豆子总颗数( )。
A.成正比例 B.成反比例 C.不成比例
19.一个三角形三个内角度数的比是7∶3∶2,这个三角形是( )。
A.锐角三角形 B.直角三角形 C.钝角三角形
四、口算和估算
20.直接写出得数。
0.58×10= 4÷0.25= = 6-=
= 1--= 3×+5×=
五、脱式计算
21.计算下面各题。
2.5×12+137
六、化简比和求比值
22.化简下面各比。
∶ 12.6∶0.4
七、解答题
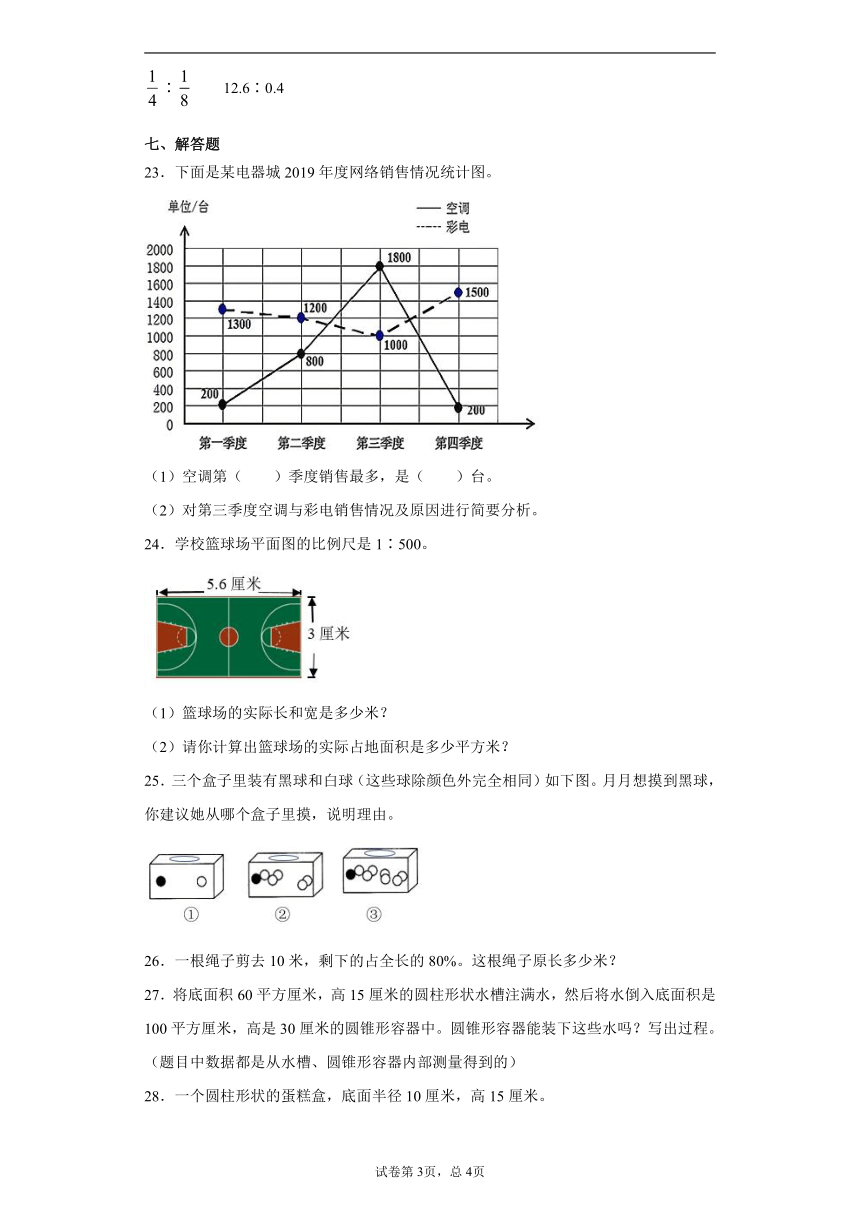
23.下面是某电器城2019年度网络销售情况统计图。
(1)空调第( )季度销售最多,是( )台。
(2)对第三季度空调与彩电销售情况及原因进行简要分析。
24.学校篮球场平面图的比例尺是1∶500。
(1)篮球场的实际长和宽是多少米?
(2)请你计算出篮球场的实际占地面积是多少平方米?
25.三个盒子里装有黑球和白球(这些球除颜色外完全相同)如下图。月月想摸到黑球,你建议她从哪个盒子里摸,说明理由。
26.一根绳子剪去10米,剩下的占全长的80%。这根绳子原长多少米?
27.将底面积60平方厘米,高15厘米的圆柱形状水槽注满水,然后将水倒入底面积是100平方厘米,高是30厘米的圆锥形容器中。圆锥形容器能装下这些水吗?写出过程。(题目中数据都是从水槽、圆锥形容器内部测量得到的)
28.一个圆柱形状的蛋糕盒,底面半径10厘米,高15厘米。
(1)做这个蛋糕盒至少需要多少平方厘米纸板?
(2)像下图那样用彩带包扎这个蛋糕盒,至少需要彩带多少厘米?(打结处大约用25厘米彩带)
29.东西两地相距420千米,甲乙两车同时从两地相对行驶,经过3.5小时相遇。甲乙两车速度的比是7︰5,相遇时乙车行了多少千米?
30.一个长方体木块,如图(单位:分米)。将它沿虚线切开,表面积增加多少平方分米?
31.暑假王华一家三口准备自驾去月坨岛旅游。如果走高速全程约270千米,需要3小时,高速收费130元。如果不走高速全程约240千米,需4小时。
(1)汽车走高速比不走高速每小时快多少千米?
(2)你建议王华一家走高速还是不走高速,请说明理由。
参考答案
1.36191 4
【分析】
(1)整数的写法:从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0,据此写出;
(2)省略“万”后面的尾数求它的近似数,要看万位的下一位千位上的数进行四舍五入,再在数的后面带上“万”字,据此解答。
【详解】
三万六千一百九十一 写作:36191;
36191≈4万;
台湾岛的面积约为三万六千一百九十一平方千米,写作36191平方千米,省略“万”后面的位数约是4万平方千米。
【点睛】
本题主要考查整数的写法和求近似数,注意求近似数时要带计数单位。
2.6
【详解】
略
3.9
【分析】
当字母的数值确定时,把它代入含有字母的式子中进行计算,所得的结果就是含有字母的式子的值。
【详解】
当a=0.6时,
b=15a
=15×0.6
=9
【点睛】
15a表示15×a。
4.18
【分析】
根据比例的性质,用内项积除以外项,就能得到另一个外项。
【详解】
12÷=18,所以另一个外项是18。
【点睛】
本题考查了比例的性质,明确比例中内项积等于外项积是解题的关键。
5.90 直角
【分析】
三角形内角和分别减去两个内角度数,就等于另一个内角度数;有一个角是直角的三角形是直角三角形。
【详解】
180°-65°-25°=90°,这是一个直角三角形。
【点睛】
解答此题应明确三角形的内角度数的和是180°,求出第三个角,然后根据三角形的分类判定类型。
6.76
【分析】
根据长方体的特征,12条棱分为互相平行(相对)的3组,每组4条棱的长度相等。求做这个长方体框架需要铁丝多少厘米,也就是求它的棱长总和,长方体的棱长总和=(长×宽+高)×4,把数据代入公式计算。
【详解】
(8+6+5)×4
=19×4
=76(厘米)
答:需要铁丝76厘米。
【点睛】
此题主要考查长方体的特征和棱长总和的计算方法。
7.12
【分析】
圆柱和圆锥底面积相等,设圆柱高为h,那么圆锥的高为3h;然后根据圆柱、圆锥体积公式即可解答。
【详解】
设圆柱高为h,圆锥的高为3h。
圆柱体积:V=Sh;
圆锥体积:V=S×3h=Sh;
由此可知,圆柱与圆锥体积相等,故圆柱体积是12立方分米。
【点睛】
此题主要考查学生对圆柱和圆锥体积公式的理解与实际应用解题。
8.;1
【分析】
将面包数量看作单位“1”,求每个小朋友分到几分之几,用1÷小朋友数量,求每人分几个面包,用面包数量÷小朋友数量。
【详解】
1÷2=
2÷2=1(个)
【点睛】
本题考查分数与除法的关系,分数的分子相当于被除数,分母相当于除数。
9.17
【分析】
写出10以内的所有质数,再相加即可.
【详解】
10以内所有的质数有:2,3,5,7.
所以:10以内所有的质数的和是:2+3+5+7=17.
故答案为17.
10.见详解
【分析】
用数轴表示数:根据数字在对应刻度上描点表示;负数在0的左侧,正数在0的右侧。
【详解】
作图如下:
【点睛】
在数轴上越靠右边的数越大,越靠左边的数越小。
11.见详解
【分析】
根据三角形和梯形的面积公式,只要梯形上下底之和与三角形的底相等,高相等即可。
【详解】
三角形底是3个格,梯形的上底可以是1格,下底2格,高2格,作图如下:
(画法不唯一)
【点睛】
三角形面积=底×高÷2,梯形面积=(上底+下底)×高÷2。
12.B
【分析】
三个连续的自然数的平均数是8,说明这3连续自然数的中间的数是8,另外的两个数为:8-1,8+1。
【详解】
8-1=7,8+1=9,
三个连续自然数的平均数是8,这三个连续自然数分别是7、8、9。
故选:B。
【点睛】
此题关键是理解三个连续自然数的平均数就是这三个连续自然数的中间的那个数。
13.A
【分析】
一个最简分数,如果分母中包含的质因数除了2和5以外,没有其他的质因数,那么这样的分数就能化成有限小数。
【详解】
A.分母5中只有质因数5;
B.分母7中只有质因数7;
C.分母15中有质因数3和5;
所以,只有可以化成有限小数。
故答案为:A
【点睛】
本题考查了分数和小数的互化,解题时可以直接利用分数化成有限小数的条件,也可以将每个分数的分子除以分母计算出对应的小数,再判断其是否是有限小数即可。
14.B
【分析】
求两个数为倍数关系时的最小公倍数:两个数为倍数关系,最小公倍数是较大的数,由此解答问题即可。
【详解】
因为甲乙两个数是非0的自然数,并且甲数是乙数的倍数,所以甲乙两数的最小公倍数是甲数;
故答案为:B。
【点睛】
此题主要考查求两个数为倍数关系时的最小公倍数:两个数为倍数关系,最小公倍数是较大的数。
15.C
【详解】
因过直线外一点有并且只有一条直线与已知直线垂直,所以过直线外一点画已知直线的垂线,可以画1条.
故选C.
16.A
【分析】
由题意可知,全厂工人总数为3+5,用“女工人数÷全厂工人总数”即可。
【详解】
3÷(3+5)
=3÷8
=37.5%;
故答案为:A。
【点睛】
求一个数是另一个数的百分之几,用除法解答。
17.B
【分析】
观察图形可知,三个图形从前面看到的图形相同,都是一行2个正方形;从上面和从左面看到的各不相同;据此即可解答问题。
【详解】
根据题干分析可得,这三个图形从前面看到的图形完全相同。
故答案为:B。
【点睛】
此题考查了从不同方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力。
18.A
【分析】
豆子总颗数×发芽率=发芽豆子的数量,据此判断发芽豆子的颗数与豆子总颗数的关系即可。
【详解】
因为豆子总颗数×发芽率=发芽豆子的数量,所以发芽豆子的颗数与豆子总颗数成正比例。
故答案为:A
【点睛】
本题考查了正比例,明确正比例的定义和形式是解题的关键。
19.C
【分析】
一个三角形三个内角度数的比是7∶3∶2,7>3+2,说明其中一个角超过了三角形内角和的一半,据此选择。
【详解】
7>3+2,说明其中一个角大于90度,是个钝角,因此这个三角形是钝角三角形。
故答案为:C
【点睛】
本题考查了按比例分配应用题,三角形内角和180度,通过比的各项所占份数,不需要求出度数即可知道是什么三角形。
20.5.8;16;12;;
;2;0;2
【详解】
略
21.167;
【分析】
根据小数乘法,以及分数四则运算法则,直接计算即可。
【详解】
2.5×12+137
=30+137
=167;
=
=
=
=
22.2∶1;63∶2
【分析】
利用比的性质,将比化简成最简整数比即可。
【详解】
∶
=(×8)∶(×8)
=2∶1
12.6∶0.4
=(12.6×10)∶(0.4×10)
=126∶4
=(126÷2)∶(4÷2)
=63∶2
23.(1)三,1800;
(2)见详解
【分析】
(1)观察统计图,直接得出相关结论即可;
(2)空调和彩电都是大型家用电器,一个家庭通常不会同时间购入2件大型家用电器,并且第三季度的温度高,对空调的需求量大,据此答题即可。
【详解】
(1)空调第三季度销售最多,是1800台。
(2)第三季度是一年中气温最高的时间段,所以对空调的需求量是最大的,很多家庭会选择在这个季度购入新的空调,这导致这个季度空调的销售量是最大的;
同时,一个家庭通常不会同时购入两件大型家电,所以这个季度的彩电销售量就有所下降。
【点睛】
本题考查了折线统计图,熟练看图并从中获取有用信息是解题的关键。
24.(1)长是28米,宽是15米
(2)420平方米
【分析】
(1)根据:图上距离÷比例尺=实际距离,列式计算即可。
(2)根据:长方形的面积=长×宽,代入数据计算。
【详解】
(1)5.6÷=2800(厘米)
2800厘米=28米
3÷=1500(厘米)
1500厘米=15米
答:这个篮球场的实际长是28米,宽是15米。
(2)28×15=420(平方米)
答:它的实际占地面积是420平方米。
【点睛】
熟练运用图上距离、比例尺、实际距离三者之间的关系。
25.①号盒子;可能性大(具体过程见详解)
【分析】
观察可知,3个盒子里的黑球数量一样,比较3个盒子球的数量,总数量越少,摸到黑球的可能性越大,或者用黑球数量÷总数量,求出3个盒子摸到黑球的可能性,比较即可。
【详解】
1÷2=,1÷6=,1÷8=,>>
月月从①号盒子里摸到黑球的可能性大,建议月月从①号盒子里摸。
【点睛】
可能性的大小与事件的基本条件和发展过程等许多因素有关。当条件对事件的发生有利时,发生的可能性就大一些。当条件对事件的发生不利时,发生的可能性就小一些。
26.50米
【分析】
剪去10米后,还剩下全长的80%,那么剪去的占全长的1-80%=20%,把全长看作单位“1”,已知单位“1”的百分之几是多少,求单位“1”用除法计算;据此解答。
【详解】
10÷(1-80%)
=10÷20%
=50(米)
答:这根绳子原长50米。
【点睛】
此题考查的是已知单位“1”的百分之几是多少,求单位“1”用除法计算。
27.能,过程见详解
【分析】
根据圆柱和圆锥的体积公式,求出圆柱形水槽和圆锥形容器的容积,比较即可。
【详解】
60×15=900(立方厘米)
100×30÷3=1000(立方厘米)
900<1000
答:圆锥形容器能装下这些水。
【点睛】
关键是掌握圆柱和圆锥的体积公式,圆柱体积=底面积×高,圆锥体积=底面积×高÷3。
28.(1)1570平方厘米;(2)235厘米
【分析】
(1)求需要的纸板的面积实际上是求圆柱的表面积,先求出圆柱体的侧面积,再求出底面的面积,侧面积+2个底面的面积=圆柱的表面积;
(2)彩带的长度是6条直径的长度,6条高的长度,再加上打结处大约用25厘米的长度。
【详解】
(1)2×3.14×10×15+3.14×102×2
=942+628
=1570(平方厘米)
答:做这个蛋糕盒至少需要1570平方厘米的纸板。
(2)10×2×6+15×6+25
=120+90+25
=235(厘米)
答:至少需要彩带235厘米。
【点睛】
此题主要考查圆柱的特征以及灵活运用圆柱的表面积公式S=2πrh+2πr2。
29.175千米
【分析】
甲乙两车相遇时,两车的路程之和恰好等于东西两地的距离。据此,列式将甲乙的速度和先求出来,再根据甲乙的速度比将乙车的速度计算出来,最后利用“路程=时间×速度”将乙车行驶的路程求出来即可。
【详解】
甲乙速度和:420÷3.5=120(千米/时)
乙速度:
120÷(7+5)×5
=120÷12×5
=10×5
=50(千米/时)
乙路程:50×3.5=175(千米)
答:相遇时乙车行了175千米。
【点睛】
本题考查了相遇问题和比的应用,解题关键在于,明确相遇时路程和恰好等于两地距离,并能够根据速度比将乙的速度求出来。
30.96平方分米
【分析】
看图可知,切开后增加了两个侧面,用宽×高×2即可。
【详解】
8×6×2=96(平方分米)
答:表面积增加96平方分米。
【点睛】
关键是熟悉长方体特征,长方体表面积=(长×宽+长×高+宽×高)×2。
31.(1)30千米
(2)见详解
【分析】
(1)根据:路程÷时间=速度,分别求出走高速和不走高速的速度,再相减即可。
(2)可以从节约时间或节约金钱两个方面去说,答案不唯一。
【详解】
(1)270÷3-240÷4
=90-60
=30(千米)
答:汽车走高速比不走高速每小时快30千米。
(2)我建议王华一家走高速,因为走高速的话可以提前1小时到达旅游地点。
【点睛】
灵活运用路程、时间、速度三者之间的关系。
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.台湾是我国领土不可分割的一部分。台湾岛的面积约为三万六千一百九十一平方千米,写作(______)平方千米,省略“万”后面的位数约是(______)万平方千米。
2.一个数既是6的因数,又是6的倍数,这个数是(________________).
3.b=15a,当a=0.6时,b=(______)。
4.在比例中,两个内项的积是12,一个外项是,另一个外项是(________)。
5.一个三角形的两个内角分别是65°和25°,另一个内角是(______)度。这个三角形是(______)三角形。
6.做一个长8厘米,宽6厘米,高5厘米的长方体框架需要铁丝____厘米。
7.一个圆柱和一个圆锥的底面积相等,圆锥的高是圆柱高的3倍,圆锥的体积是12立方分米,圆柱的体积是(______)立方分米。
8.把2个面包平均分给2个小朋友,每个小朋友分到这些面包的,每人分得( )个面包。
9.10以内所有的质数的和是_____.
二、作图题
10.把﹣0.5、、2在直线上表示出来。
11.在下面的方格图中画一个与三角形面积相等的梯形。
三、选择题
12.三个连续自然数的平均数是8,这三个连续自然数分别是( )。
A.6、7、8 B.7、8、9 C.8、9、10
13.下面分数能化成有限小数的是( )。
A. B. C.
14.甲、乙两数都是非0自然数,如果甲数是乙数的倍数,那么甲数和乙数的最小公倍数是( )。
A.乙数 B.甲数 C.甲、乙两数的乘积
15.过直线外一点能画( )已知直线的垂线
A.无数条 B.两条 C.一条
16.某工厂女工人数与男工人数比是3∶5,女工人数是全厂工人总数的( )。
A.37.5% B.60% C.62.5%
17.下面三个立体图形从( )面看到的形状完全一样。
A.上面 B.前面 C.左面
18.豆芽的发芽率一定,发芽豆子的颗数与豆子总颗数( )。
A.成正比例 B.成反比例 C.不成比例
19.一个三角形三个内角度数的比是7∶3∶2,这个三角形是( )。
A.锐角三角形 B.直角三角形 C.钝角三角形
四、口算和估算
20.直接写出得数。
0.58×10= 4÷0.25= = 6-=
= 1--= 3×+5×=
五、脱式计算
21.计算下面各题。
2.5×12+137
六、化简比和求比值
22.化简下面各比。
∶ 12.6∶0.4
七、解答题
23.下面是某电器城2019年度网络销售情况统计图。
(1)空调第( )季度销售最多,是( )台。
(2)对第三季度空调与彩电销售情况及原因进行简要分析。
24.学校篮球场平面图的比例尺是1∶500。
(1)篮球场的实际长和宽是多少米?
(2)请你计算出篮球场的实际占地面积是多少平方米?
25.三个盒子里装有黑球和白球(这些球除颜色外完全相同)如下图。月月想摸到黑球,你建议她从哪个盒子里摸,说明理由。
26.一根绳子剪去10米,剩下的占全长的80%。这根绳子原长多少米?
27.将底面积60平方厘米,高15厘米的圆柱形状水槽注满水,然后将水倒入底面积是100平方厘米,高是30厘米的圆锥形容器中。圆锥形容器能装下这些水吗?写出过程。(题目中数据都是从水槽、圆锥形容器内部测量得到的)
28.一个圆柱形状的蛋糕盒,底面半径10厘米,高15厘米。
(1)做这个蛋糕盒至少需要多少平方厘米纸板?
(2)像下图那样用彩带包扎这个蛋糕盒,至少需要彩带多少厘米?(打结处大约用25厘米彩带)
29.东西两地相距420千米,甲乙两车同时从两地相对行驶,经过3.5小时相遇。甲乙两车速度的比是7︰5,相遇时乙车行了多少千米?
30.一个长方体木块,如图(单位:分米)。将它沿虚线切开,表面积增加多少平方分米?
31.暑假王华一家三口准备自驾去月坨岛旅游。如果走高速全程约270千米,需要3小时,高速收费130元。如果不走高速全程约240千米,需4小时。
(1)汽车走高速比不走高速每小时快多少千米?
(2)你建议王华一家走高速还是不走高速,请说明理由。
参考答案
1.36191 4
【分析】
(1)整数的写法:从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0,据此写出;
(2)省略“万”后面的尾数求它的近似数,要看万位的下一位千位上的数进行四舍五入,再在数的后面带上“万”字,据此解答。
【详解】
三万六千一百九十一 写作:36191;
36191≈4万;
台湾岛的面积约为三万六千一百九十一平方千米,写作36191平方千米,省略“万”后面的位数约是4万平方千米。
【点睛】
本题主要考查整数的写法和求近似数,注意求近似数时要带计数单位。
2.6
【详解】
略
3.9
【分析】
当字母的数值确定时,把它代入含有字母的式子中进行计算,所得的结果就是含有字母的式子的值。
【详解】
当a=0.6时,
b=15a
=15×0.6
=9
【点睛】
15a表示15×a。
4.18
【分析】
根据比例的性质,用内项积除以外项,就能得到另一个外项。
【详解】
12÷=18,所以另一个外项是18。
【点睛】
本题考查了比例的性质,明确比例中内项积等于外项积是解题的关键。
5.90 直角
【分析】
三角形内角和分别减去两个内角度数,就等于另一个内角度数;有一个角是直角的三角形是直角三角形。
【详解】
180°-65°-25°=90°,这是一个直角三角形。
【点睛】
解答此题应明确三角形的内角度数的和是180°,求出第三个角,然后根据三角形的分类判定类型。
6.76
【分析】
根据长方体的特征,12条棱分为互相平行(相对)的3组,每组4条棱的长度相等。求做这个长方体框架需要铁丝多少厘米,也就是求它的棱长总和,长方体的棱长总和=(长×宽+高)×4,把数据代入公式计算。
【详解】
(8+6+5)×4
=19×4
=76(厘米)
答:需要铁丝76厘米。
【点睛】
此题主要考查长方体的特征和棱长总和的计算方法。
7.12
【分析】
圆柱和圆锥底面积相等,设圆柱高为h,那么圆锥的高为3h;然后根据圆柱、圆锥体积公式即可解答。
【详解】
设圆柱高为h,圆锥的高为3h。
圆柱体积:V=Sh;
圆锥体积:V=S×3h=Sh;
由此可知,圆柱与圆锥体积相等,故圆柱体积是12立方分米。
【点睛】
此题主要考查学生对圆柱和圆锥体积公式的理解与实际应用解题。
8.;1
【分析】
将面包数量看作单位“1”,求每个小朋友分到几分之几,用1÷小朋友数量,求每人分几个面包,用面包数量÷小朋友数量。
【详解】
1÷2=
2÷2=1(个)
【点睛】
本题考查分数与除法的关系,分数的分子相当于被除数,分母相当于除数。
9.17
【分析】
写出10以内的所有质数,再相加即可.
【详解】
10以内所有的质数有:2,3,5,7.
所以:10以内所有的质数的和是:2+3+5+7=17.
故答案为17.
10.见详解
【分析】
用数轴表示数:根据数字在对应刻度上描点表示;负数在0的左侧,正数在0的右侧。
【详解】
作图如下:
【点睛】
在数轴上越靠右边的数越大,越靠左边的数越小。
11.见详解
【分析】
根据三角形和梯形的面积公式,只要梯形上下底之和与三角形的底相等,高相等即可。
【详解】
三角形底是3个格,梯形的上底可以是1格,下底2格,高2格,作图如下:
(画法不唯一)
【点睛】
三角形面积=底×高÷2,梯形面积=(上底+下底)×高÷2。
12.B
【分析】
三个连续的自然数的平均数是8,说明这3连续自然数的中间的数是8,另外的两个数为:8-1,8+1。
【详解】
8-1=7,8+1=9,
三个连续自然数的平均数是8,这三个连续自然数分别是7、8、9。
故选:B。
【点睛】
此题关键是理解三个连续自然数的平均数就是这三个连续自然数的中间的那个数。
13.A
【分析】
一个最简分数,如果分母中包含的质因数除了2和5以外,没有其他的质因数,那么这样的分数就能化成有限小数。
【详解】
A.分母5中只有质因数5;
B.分母7中只有质因数7;
C.分母15中有质因数3和5;
所以,只有可以化成有限小数。
故答案为:A
【点睛】
本题考查了分数和小数的互化,解题时可以直接利用分数化成有限小数的条件,也可以将每个分数的分子除以分母计算出对应的小数,再判断其是否是有限小数即可。
14.B
【分析】
求两个数为倍数关系时的最小公倍数:两个数为倍数关系,最小公倍数是较大的数,由此解答问题即可。
【详解】
因为甲乙两个数是非0的自然数,并且甲数是乙数的倍数,所以甲乙两数的最小公倍数是甲数;
故答案为:B。
【点睛】
此题主要考查求两个数为倍数关系时的最小公倍数:两个数为倍数关系,最小公倍数是较大的数。
15.C
【详解】
因过直线外一点有并且只有一条直线与已知直线垂直,所以过直线外一点画已知直线的垂线,可以画1条.
故选C.
16.A
【分析】
由题意可知,全厂工人总数为3+5,用“女工人数÷全厂工人总数”即可。
【详解】
3÷(3+5)
=3÷8
=37.5%;
故答案为:A。
【点睛】
求一个数是另一个数的百分之几,用除法解答。
17.B
【分析】
观察图形可知,三个图形从前面看到的图形相同,都是一行2个正方形;从上面和从左面看到的各不相同;据此即可解答问题。
【详解】
根据题干分析可得,这三个图形从前面看到的图形完全相同。
故答案为:B。
【点睛】
此题考查了从不同方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力。
18.A
【分析】
豆子总颗数×发芽率=发芽豆子的数量,据此判断发芽豆子的颗数与豆子总颗数的关系即可。
【详解】
因为豆子总颗数×发芽率=发芽豆子的数量,所以发芽豆子的颗数与豆子总颗数成正比例。
故答案为:A
【点睛】
本题考查了正比例,明确正比例的定义和形式是解题的关键。
19.C
【分析】
一个三角形三个内角度数的比是7∶3∶2,7>3+2,说明其中一个角超过了三角形内角和的一半,据此选择。
【详解】
7>3+2,说明其中一个角大于90度,是个钝角,因此这个三角形是钝角三角形。
故答案为:C
【点睛】
本题考查了按比例分配应用题,三角形内角和180度,通过比的各项所占份数,不需要求出度数即可知道是什么三角形。
20.5.8;16;12;;
;2;0;2
【详解】
略
21.167;
【分析】
根据小数乘法,以及分数四则运算法则,直接计算即可。
【详解】
2.5×12+137
=30+137
=167;
=
=
=
=
22.2∶1;63∶2
【分析】
利用比的性质,将比化简成最简整数比即可。
【详解】
∶
=(×8)∶(×8)
=2∶1
12.6∶0.4
=(12.6×10)∶(0.4×10)
=126∶4
=(126÷2)∶(4÷2)
=63∶2
23.(1)三,1800;
(2)见详解
【分析】
(1)观察统计图,直接得出相关结论即可;
(2)空调和彩电都是大型家用电器,一个家庭通常不会同时间购入2件大型家用电器,并且第三季度的温度高,对空调的需求量大,据此答题即可。
【详解】
(1)空调第三季度销售最多,是1800台。
(2)第三季度是一年中气温最高的时间段,所以对空调的需求量是最大的,很多家庭会选择在这个季度购入新的空调,这导致这个季度空调的销售量是最大的;
同时,一个家庭通常不会同时购入两件大型家电,所以这个季度的彩电销售量就有所下降。
【点睛】
本题考查了折线统计图,熟练看图并从中获取有用信息是解题的关键。
24.(1)长是28米,宽是15米
(2)420平方米
【分析】
(1)根据:图上距离÷比例尺=实际距离,列式计算即可。
(2)根据:长方形的面积=长×宽,代入数据计算。
【详解】
(1)5.6÷=2800(厘米)
2800厘米=28米
3÷=1500(厘米)
1500厘米=15米
答:这个篮球场的实际长是28米,宽是15米。
(2)28×15=420(平方米)
答:它的实际占地面积是420平方米。
【点睛】
熟练运用图上距离、比例尺、实际距离三者之间的关系。
25.①号盒子;可能性大(具体过程见详解)
【分析】
观察可知,3个盒子里的黑球数量一样,比较3个盒子球的数量,总数量越少,摸到黑球的可能性越大,或者用黑球数量÷总数量,求出3个盒子摸到黑球的可能性,比较即可。
【详解】
1÷2=,1÷6=,1÷8=,>>
月月从①号盒子里摸到黑球的可能性大,建议月月从①号盒子里摸。
【点睛】
可能性的大小与事件的基本条件和发展过程等许多因素有关。当条件对事件的发生有利时,发生的可能性就大一些。当条件对事件的发生不利时,发生的可能性就小一些。
26.50米
【分析】
剪去10米后,还剩下全长的80%,那么剪去的占全长的1-80%=20%,把全长看作单位“1”,已知单位“1”的百分之几是多少,求单位“1”用除法计算;据此解答。
【详解】
10÷(1-80%)
=10÷20%
=50(米)
答:这根绳子原长50米。
【点睛】
此题考查的是已知单位“1”的百分之几是多少,求单位“1”用除法计算。
27.能,过程见详解
【分析】
根据圆柱和圆锥的体积公式,求出圆柱形水槽和圆锥形容器的容积,比较即可。
【详解】
60×15=900(立方厘米)
100×30÷3=1000(立方厘米)
900<1000
答:圆锥形容器能装下这些水。
【点睛】
关键是掌握圆柱和圆锥的体积公式,圆柱体积=底面积×高,圆锥体积=底面积×高÷3。
28.(1)1570平方厘米;(2)235厘米
【分析】
(1)求需要的纸板的面积实际上是求圆柱的表面积,先求出圆柱体的侧面积,再求出底面的面积,侧面积+2个底面的面积=圆柱的表面积;
(2)彩带的长度是6条直径的长度,6条高的长度,再加上打结处大约用25厘米的长度。
【详解】
(1)2×3.14×10×15+3.14×102×2
=942+628
=1570(平方厘米)
答:做这个蛋糕盒至少需要1570平方厘米的纸板。
(2)10×2×6+15×6+25
=120+90+25
=235(厘米)
答:至少需要彩带235厘米。
【点睛】
此题主要考查圆柱的特征以及灵活运用圆柱的表面积公式S=2πrh+2πr2。
29.175千米
【分析】
甲乙两车相遇时,两车的路程之和恰好等于东西两地的距离。据此,列式将甲乙的速度和先求出来,再根据甲乙的速度比将乙车的速度计算出来,最后利用“路程=时间×速度”将乙车行驶的路程求出来即可。
【详解】
甲乙速度和:420÷3.5=120(千米/时)
乙速度:
120÷(7+5)×5
=120÷12×5
=10×5
=50(千米/时)
乙路程:50×3.5=175(千米)
答:相遇时乙车行了175千米。
【点睛】
本题考查了相遇问题和比的应用,解题关键在于,明确相遇时路程和恰好等于两地距离,并能够根据速度比将乙的速度求出来。
30.96平方分米
【分析】
看图可知,切开后增加了两个侧面,用宽×高×2即可。
【详解】
8×6×2=96(平方分米)
答:表面积增加96平方分米。
【点睛】
关键是熟悉长方体特征,长方体表面积=(长×宽+长×高+宽×高)×2。
31.(1)30千米
(2)见详解
【分析】
(1)根据:路程÷时间=速度,分别求出走高速和不走高速的速度,再相减即可。
(2)可以从节约时间或节约金钱两个方面去说,答案不唯一。
【详解】
(1)270÷3-240÷4
=90-60
=30(千米)
答:汽车走高速比不走高速每小时快30千米。
(2)我建议王华一家走高速,因为走高速的话可以提前1小时到达旅游地点。
【点睛】
灵活运用路程、时间、速度三者之间的关系。
同课章节目录
