苏科版七年级下册导学案:§7.3图形的平移(无答案)
文档属性
| 名称 | 苏科版七年级下册导学案:§7.3图形的平移(无答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 75.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 00:00:00 | ||
图片预览

文档简介
《§7.3图形的平移》 学导单 班级______ 姓名___________
【学习目标】:
1.通过预习认识图形的平移,探索图形的平移的基本性质.
2、了解平移的方向和距离的概念,小组合作、会画平移图形.
【学习重点】图形的平移的概念及基本性质.
【旧知回顾】
小学我们已经学习平移,请你例举生活中的平移实例.
【活动探究一】
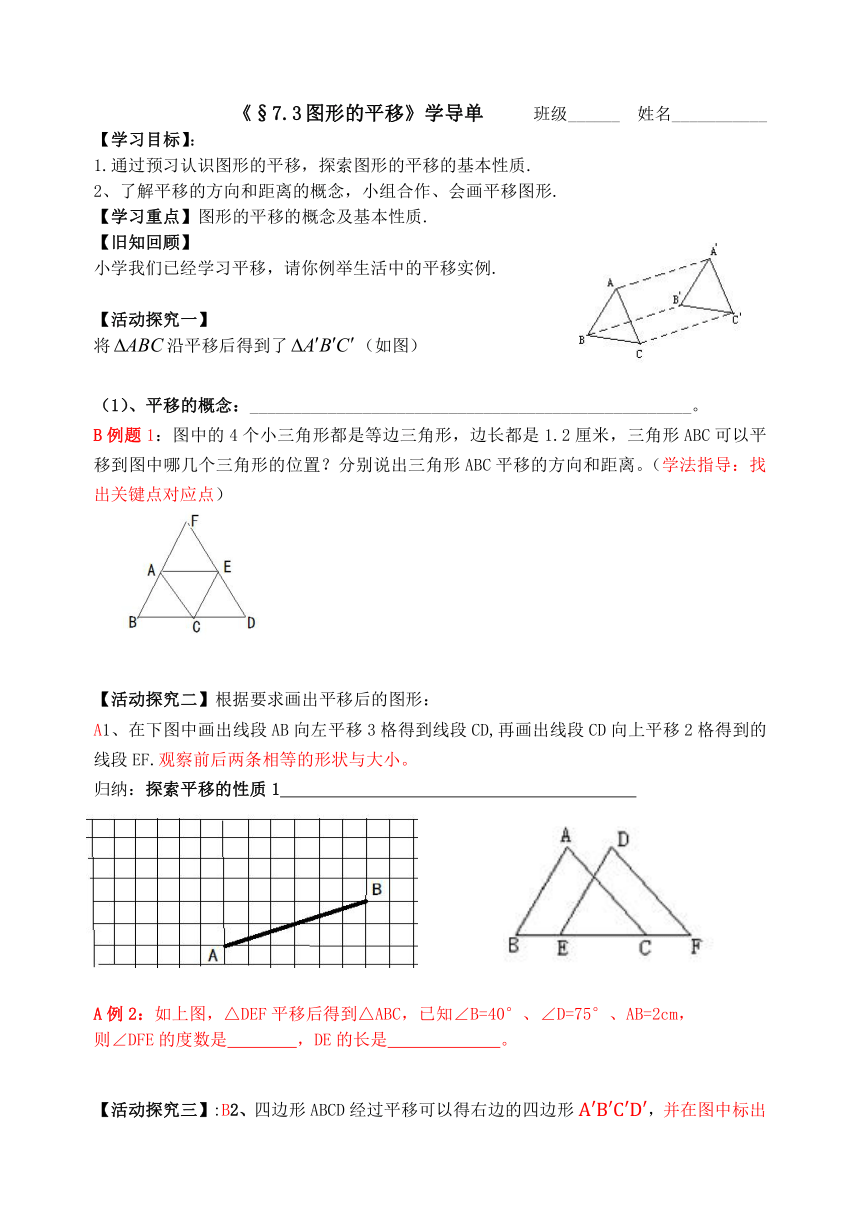
将沿平移后得到了(如图)
(1)、平移的概念:___________________________________________________。
B例题1:图中的4个小三角形都是等边三角形,边长都是1.2厘米,三角形ABC可以平移到图中哪几个三角形的位置?分别说出三角形ABC平移的方向和距离。(学法指导:找出关键点对应点)
【活动探究二】根据要求画出平移后的图形:
A1、在下图中画出线段AB向左平移3格得到线段CD,再画出线段CD向上平移2格得到的线段EF.观察前后两条相等的形状与大小。
归纳:探索平移的性质1
A例2:如上图,△DEF平移后得到△ABC,已知∠B=40°、∠D=75°、AB=2cm,
则∠DFE的度数是 ,DE的长是 。
【活动探究三】:B2、四边形ABCD经过平移可以得右边的四边形A′B′C′D′,并在图中标出对应字母位置,连接对应点,你能发现各组对应点的连线之间的关系(位置、大小)吗?
归纳:探索平移的性质2
B例题3:平移图形中的三角形ABC,使点A移到A’的位置,画出平移后所得的三角形。
A例题4:如下图,在每个小正方形边长为1的方格纸中, △ABC的顶点
都在方格纸格点上.
(1)将△ABC经过平移后得到△A′B′C′,图中标出了点B的
对应点B',补全△A′B′C′;
(2)若连接AA′,BB′,则这两条线段之间的关系是 ;
拓展:C(3)△ABC的面积为 ;
(4)在图中画出△A′B′C′的高A′D;
【拓展提高】
B1.如图:长方形ABCD中, BC=10,AB=8,则图中五个长方形的周长之和为 .
B 2.某中学校园内有一块长30m,宽22m的草坪,中间有两条宽2m的小路,把草坪分成了4块,如图所示,则草坪的面积 .
C3.如图,由2个边长为6的正方形拼成一个长方形.
(1)求图中阴影部分的面积;
(2)你能用平移的方法很快求出阴影部分的面积吗?
试试看平移前的图形与平移后的图形之间有何联系?
《§7.3图形的平移》课堂检测单
1.(A)下列现象:①手扶电梯的人,②飞机在地面上沿直线滑行,③风车的转动,④冷水加热过程中气泡的上升⑤鼠标拖动的图片其中属于平移的是( )
A、①②⑤ B、①③⑤ C、②③ D、③④
2.(A)如图,O是长方形的对角线AC的中点,OE⊥AB,OF⊥BC,垂足分别为E、F,若AC=3cm,则将△OFC沿CA方向平移______cm可以得到三角形AEO。
3.(B)如图,是由8个边长均为2cm的小正方形组成的长方形,图中阴影部分的面积是_______cm2。
4.(A)在如图的方格纸上,平移所给的三角形,使点A到点A′的位置。
B5.某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( )
A.甲种方案所用铁丝最长 B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长 D.三种方案所用铁丝一样长
【学习目标】:
1.通过预习认识图形的平移,探索图形的平移的基本性质.
2、了解平移的方向和距离的概念,小组合作、会画平移图形.
【学习重点】图形的平移的概念及基本性质.
【旧知回顾】
小学我们已经学习平移,请你例举生活中的平移实例.
【活动探究一】
将沿平移后得到了(如图)
(1)、平移的概念:___________________________________________________。
B例题1:图中的4个小三角形都是等边三角形,边长都是1.2厘米,三角形ABC可以平移到图中哪几个三角形的位置?分别说出三角形ABC平移的方向和距离。(学法指导:找出关键点对应点)
【活动探究二】根据要求画出平移后的图形:
A1、在下图中画出线段AB向左平移3格得到线段CD,再画出线段CD向上平移2格得到的线段EF.观察前后两条相等的形状与大小。
归纳:探索平移的性质1
A例2:如上图,△DEF平移后得到△ABC,已知∠B=40°、∠D=75°、AB=2cm,
则∠DFE的度数是 ,DE的长是 。
【活动探究三】:B2、四边形ABCD经过平移可以得右边的四边形A′B′C′D′,并在图中标出对应字母位置,连接对应点,你能发现各组对应点的连线之间的关系(位置、大小)吗?
归纳:探索平移的性质2
B例题3:平移图形中的三角形ABC,使点A移到A’的位置,画出平移后所得的三角形。
A例题4:如下图,在每个小正方形边长为1的方格纸中, △ABC的顶点
都在方格纸格点上.
(1)将△ABC经过平移后得到△A′B′C′,图中标出了点B的
对应点B',补全△A′B′C′;
(2)若连接AA′,BB′,则这两条线段之间的关系是 ;
拓展:C(3)△ABC的面积为 ;
(4)在图中画出△A′B′C′的高A′D;
【拓展提高】
B1.如图:长方形ABCD中, BC=10,AB=8,则图中五个长方形的周长之和为 .
B 2.某中学校园内有一块长30m,宽22m的草坪,中间有两条宽2m的小路,把草坪分成了4块,如图所示,则草坪的面积 .
C3.如图,由2个边长为6的正方形拼成一个长方形.
(1)求图中阴影部分的面积;
(2)你能用平移的方法很快求出阴影部分的面积吗?
试试看平移前的图形与平移后的图形之间有何联系?
《§7.3图形的平移》课堂检测单
1.(A)下列现象:①手扶电梯的人,②飞机在地面上沿直线滑行,③风车的转动,④冷水加热过程中气泡的上升⑤鼠标拖动的图片其中属于平移的是( )
A、①②⑤ B、①③⑤ C、②③ D、③④
2.(A)如图,O是长方形的对角线AC的中点,OE⊥AB,OF⊥BC,垂足分别为E、F,若AC=3cm,则将△OFC沿CA方向平移______cm可以得到三角形AEO。
3.(B)如图,是由8个边长均为2cm的小正方形组成的长方形,图中阴影部分的面积是_______cm2。
4.(A)在如图的方格纸上,平移所给的三角形,使点A到点A′的位置。
B5.某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( )
A.甲种方案所用铁丝最长 B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长 D.三种方案所用铁丝一样长
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
