人教版数学七年级下册 6.1.2 用计算器求一个正数的算数平方根 课件(20张)
文档属性
| 名称 | 人教版数学七年级下册 6.1.2 用计算器求一个正数的算数平方根 课件(20张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 633.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 00:00:00 | ||
图片预览








文档简介
第六章 实数
6.1 平方根
课时2 用计算器求一个正数的算数平方根
估算
用计算器求一个正数的算术平方根. (重点、难点)
学习目标
新课导入
你能计算 吗?
新课讲解
知识点1 估算
探究1
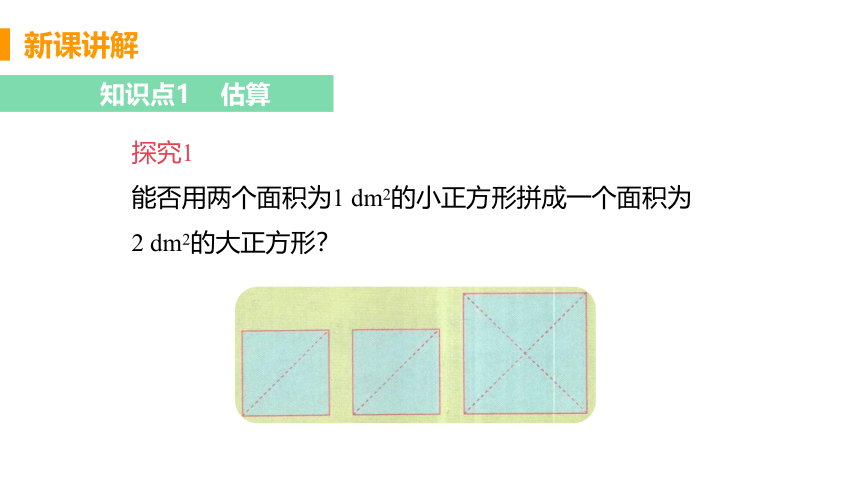
能否用两个面积为1 dm2的小正方形拼成一个面积为
2 dm2的大正方形?
新课讲解
如图,把两个小正方形分别沿对角线剪开,将所得的4
个直角三角形拼在一起,就得到一个面积为2 dm2的大
正方形. 你知道这个大正方形的边长是多少吗?
设大正方形的边长为x dm,则x2 = 2.
由算术平方根的意义可知x= ,
所以大正方形的边长是 dm.
新课讲解
探究2 有多大?
因为 12 = 1,22=4,所以1< <2;
因为 1. 42 = 1. 96,1. 52=2. 25,所以 1.4< <1.5;
因为 1.412 = 1.988 1,1.422 = 2.016 4,
所以 1.41< <1.42;
因为 1. 4142 = 1. 999 396,1. 4152=2. 002 225,
所以 1.414< <1.415;
……
新课讲解
如此进行下去,可以得到 的更精确的近似值. 事实
上, =1. 414 213 562 373…,它是一 个无限不循环
小数.
实际上,许多正有理数的算术平方根(例如
等)都是无限不循环小数.
新课讲解
例
典例分析
小丽想用一块面积为 400 cm2
的正方形纸片,沿着边的方
向裁出一块面积为 300 cm2的
长方形纸片,使它的长宽之
比为 3: 2. 她不知能否裁得出
来,正在发愁. 小明见了说:“别发愁,一定能用一块 面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?
新课讲解
解:
设长方形纸片的长为3x cm,宽为2x cm. 根据边长
与面积的关系得
3x ? 2x=300,6x2 =300, x2 =50, x = .
因此长方形纸片的长为 cm.
因为50>49,所以 >7.
由上可知 >21,即长方形纸片的长应该大
于21 cm.
因为 =20,所以正方形纸片的边长只有20 cm.
这样,长方形纸片的长将大于正方形纸片的边长.
答:不能同意小明的说法.
小丽不能用这块正方形纸片裁出符合要求的长方形纸片.
新课讲解
练一练
比较下列各组数的大小:
解:
(1)因为 ≈2.83, ≈3.16,所以 < ;
(2)因为 ≈8.06,所以 >8;
(3)因为 ≈0.62,所以 >0.5;
(4)由(3)知 <1.
新课讲解
知识点2 用计算器求一个正数的算术平方根
请同学们互相看一下各自的计算器,拿同一类型
计算器的同学坐到一起,这样便于讨论问题. 请同学
们看下图中所示的计算器,我们首先来熟悉一下这个
计算器的操作程序,如果你的计算器与这个计算器是
同一类型的话,
可以操作一下,
其余的同学看
看操作步骤.
新课讲解
大多数计算器都有 键,用它可以求出一个正
数的算术平方根(或其近似值),应注意的是,不同型
号的计算器按键的顺序可能不同,使用计算器时,一
定要按照说明书进行操作.
新课讲解
例
典例分析
用计算器求下列各式的值:
(1) ; (2) (精确到 0.001).
解:
(1)依次按键 3136 ,
显示:56.
∴ =56.
(2)依次按键, 2 ,
显示:1.414 213 562.
∴ ≈1.414.
新课讲解
练一练
用计算器求下列各式的值:
(1) ; (2) ; (3) (精确到 0.01).
解:
新课讲解
用计算器计算,若按键顺序为
,则相应的算式是( )
A. ×5-0×5÷2= B.( ×5-0×5)÷2=
C. -0.5÷2= D.( -0.5)÷2=
4
·
5
-
0
·
5
÷
2
=
C
课堂小结
1. 利用计算器求一个正数的算术平方根,有时它的
算术平方根是准确数,有时它的算术平方根是近
似数.
2. 采用算术平方根比较法比较大小时,被开方数大
的算术平方根就大;即若a≥b≥0时, ≥ ≥0;
反之亦成立.
当堂小练
1.若A.1C.2B
当堂小练
2.计算 的结果精确到0.01是(可用科学计算器计算或笔算)( )
A.0.30 B.0.31
C.0.32 D.0.33
C
拓展与延伸
已知 ≈4.80, ≈15.17,则 的值
约为( )
A.0.480 B.0.048 0
C.0.151 7 D.1.517
B
分析:0.002 3是由23的小数点向左移动四位得到的,则它的算术平方根是由 的小数点向左移动两位得到的.
布置作业
请完成对应习题
6.1 平方根
课时2 用计算器求一个正数的算数平方根
估算
用计算器求一个正数的算术平方根. (重点、难点)
学习目标
新课导入
你能计算 吗?
新课讲解
知识点1 估算
探究1
能否用两个面积为1 dm2的小正方形拼成一个面积为
2 dm2的大正方形?
新课讲解
如图,把两个小正方形分别沿对角线剪开,将所得的4
个直角三角形拼在一起,就得到一个面积为2 dm2的大
正方形. 你知道这个大正方形的边长是多少吗?
设大正方形的边长为x dm,则x2 = 2.
由算术平方根的意义可知x= ,
所以大正方形的边长是 dm.
新课讲解
探究2 有多大?
因为 12 = 1,22=4,所以1< <2;
因为 1. 42 = 1. 96,1. 52=2. 25,所以 1.4< <1.5;
因为 1.412 = 1.988 1,1.422 = 2.016 4,
所以 1.41< <1.42;
因为 1. 4142 = 1. 999 396,1. 4152=2. 002 225,
所以 1.414< <1.415;
……
新课讲解
如此进行下去,可以得到 的更精确的近似值. 事实
上, =1. 414 213 562 373…,它是一 个无限不循环
小数.
实际上,许多正有理数的算术平方根(例如
等)都是无限不循环小数.
新课讲解
例
典例分析
小丽想用一块面积为 400 cm2
的正方形纸片,沿着边的方
向裁出一块面积为 300 cm2的
长方形纸片,使它的长宽之
比为 3: 2. 她不知能否裁得出
来,正在发愁. 小明见了说:“别发愁,一定能用一块 面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?
新课讲解
解:
设长方形纸片的长为3x cm,宽为2x cm. 根据边长
与面积的关系得
3x ? 2x=300,6x2 =300, x2 =50, x = .
因此长方形纸片的长为 cm.
因为50>49,所以 >7.
由上可知 >21,即长方形纸片的长应该大
于21 cm.
因为 =20,所以正方形纸片的边长只有20 cm.
这样,长方形纸片的长将大于正方形纸片的边长.
答:不能同意小明的说法.
小丽不能用这块正方形纸片裁出符合要求的长方形纸片.
新课讲解
练一练
比较下列各组数的大小:
解:
(1)因为 ≈2.83, ≈3.16,所以 < ;
(2)因为 ≈8.06,所以 >8;
(3)因为 ≈0.62,所以 >0.5;
(4)由(3)知 <1.
新课讲解
知识点2 用计算器求一个正数的算术平方根
请同学们互相看一下各自的计算器,拿同一类型
计算器的同学坐到一起,这样便于讨论问题. 请同学
们看下图中所示的计算器,我们首先来熟悉一下这个
计算器的操作程序,如果你的计算器与这个计算器是
同一类型的话,
可以操作一下,
其余的同学看
看操作步骤.
新课讲解
大多数计算器都有 键,用它可以求出一个正
数的算术平方根(或其近似值),应注意的是,不同型
号的计算器按键的顺序可能不同,使用计算器时,一
定要按照说明书进行操作.
新课讲解
例
典例分析
用计算器求下列各式的值:
(1) ; (2) (精确到 0.001).
解:
(1)依次按键 3136 ,
显示:56.
∴ =56.
(2)依次按键, 2 ,
显示:1.414 213 562.
∴ ≈1.414.
新课讲解
练一练
用计算器求下列各式的值:
(1) ; (2) ; (3) (精确到 0.01).
解:
新课讲解
用计算器计算,若按键顺序为
,则相应的算式是( )
A. ×5-0×5÷2= B.( ×5-0×5)÷2=
C. -0.5÷2= D.( -0.5)÷2=
4
·
5
-
0
·
5
÷
2
=
C
课堂小结
1. 利用计算器求一个正数的算术平方根,有时它的
算术平方根是准确数,有时它的算术平方根是近
似数.
2. 采用算术平方根比较法比较大小时,被开方数大
的算术平方根就大;即若a≥b≥0时, ≥ ≥0;
反之亦成立.
当堂小练
1.若
当堂小练
2.计算 的结果精确到0.01是(可用科学计算器计算或笔算)( )
A.0.30 B.0.31
C.0.32 D.0.33
C
拓展与延伸
已知 ≈4.80, ≈15.17,则 的值
约为( )
A.0.480 B.0.048 0
C.0.151 7 D.1.517
B
分析:0.002 3是由23的小数点向左移动四位得到的,则它的算术平方根是由 的小数点向左移动两位得到的.
布置作业
请完成对应习题
