人教版数学七年级下册 6.3.2 实数的运算 课件(24张)
文档属性
| 名称 | 人教版数学七年级下册 6.3.2 实数的运算 课件(24张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 368.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 00:00:00 | ||
图片预览







文档简介
第六章 实数
6.3 实数
课时2 实数的运算
实数的性质
实数的大小比较
实数的运算(重点、难点)
学习目标
新课导入
把有理数扩充到实数之后,有理数关于相反数和绝对值的意义,大小比较以及运算法则和运算律等同样适合于实数,这节课我们就来学习这些内容.
新课讲解
知识点1 实数的性质
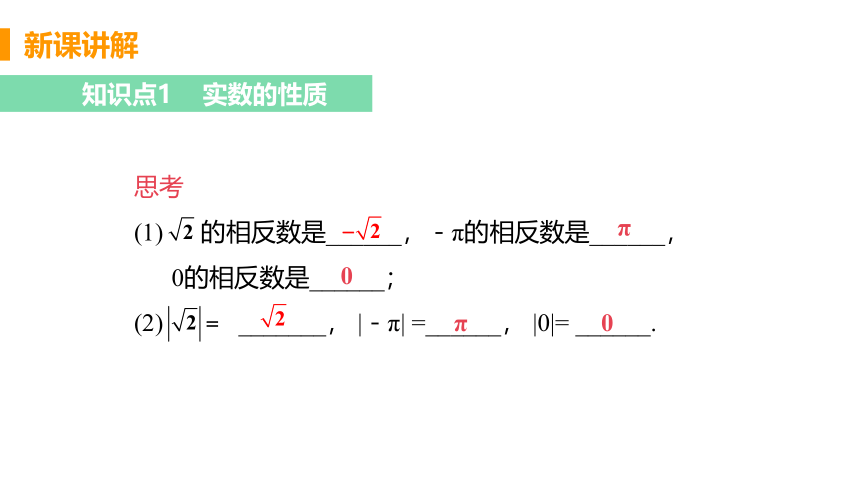
思考
(1) 的相反数是______,-π的相反数是______,
0的相反数是______;
(2) _______, |-π| =______, |0|= ______.
π
0
π
0
新课讲解
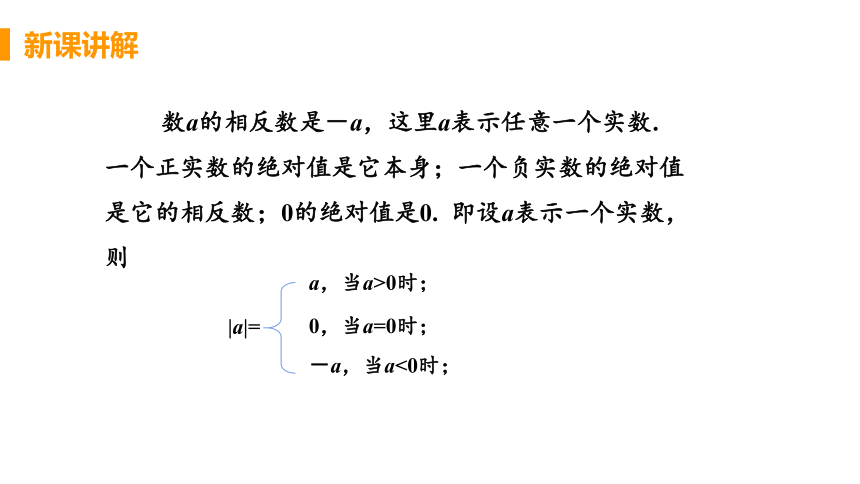
数a的相反数是-a,这里a表示任意一个实数.
一个正实数的绝对值是它本身;一个负实数的绝对值
是它的相反数;0的绝对值是0. 即设a表示一个实数,
则
|a|=
a,当a>0时;
0,当a=0时;
-a,当a<0时;
新课讲解
例
典例分析
(1)分别写出 , 的相反数;
(2)指出 , 分别是什么数的相反数;
(3)求 的绝对值;
(4)已知一个数的绝对值是 ,求这个数.
新课讲解
(1)因为 ,
所以 的相反数分别为 ;
(2)因为 ,
所以 分别是 的相反数;
(3)因为 ,
所以 ;
(4)因为 ,
所以绝对值为 的数是 或 .
解:
新课讲解
练一练
1.求下列各数的相反数与绝对值:
2.5, , , ,0.
2.5的相反数是-2.5,绝对值是2.5;
- 的相反数是 ,绝对值是 ;
- 的相反数是 ,绝对值是 ;
的相反数是 ,绝对值是 ;
0的相反数是0,绝对值是0.
解:
新课讲解
2.求下列各式中的实数x:
|x|= ; (2) |x|=0;
(3) |x|= ; (4) |x|=π .
(1)x=± ; (2)x=0;
(3)x=± ; (4)x=±π.
解:
新课讲解
知识点2 实数的大小比较
利用数轴比较实数的大小:对于数轴上的任意
两个点,右边的点表示的实数总比左边的点表示的
实数大.
新课讲解
例
典例分析
用“<”连接下列各数:- , ,-2 ,2.5,0.
分析:
比较一组实数的大小和比较一组有理数的大小
一样,可先求出这些数的近似数,再将这些数
在数轴上表示出来,然后根据“在数轴上右边
的点表示的数总比左边的点表示的数大”求解.
新课讲解
解:
将各数的大致位置在数轴上表示出来,如图所
示.
由图可知,各数用“<”可以连接成:-2
<- <0< <2.5.
新课讲解
练一练
1.下列四个数:-3,- ,-π,-1,其中最小的数是( )
A.-π B.-3
C.-1 D.-
A
新课讲解
知识点3 实数的运算
1.在实数范围内,进行加、减、乘、除、乘方和开方运
算时,有理数的运算法则和运算律仍然适用;实数混
合运算的运算顺序与有理数的混合运算顺序一样,先
算乘方、开方,再算乘除,最后算加减,同级运算按
照自左向右的顺序进行,有括号的先算括号里面的.
新课讲解
2. 有理数的运算律在实数范围内仍然适用,在进行
实数运算的过程中,要做到:
一“看”——看算式的结构特点,能否运用运算
律或公式;
二“用”——运用运算律或公式;
三“查”——检查过程和结果是否正确.
新课讲解
3.计算结果中若包含开方开不尽的数,则保留根号,
结果要化为最简形式.
学法指南:实数的运算律
加法交换律:a+b=b+a;
加法结合律:(a+b)+c=a+(b+c);
乘法交换律:ab=ba;
乘法结合律:(ab)c=a(bc);
乘法分配律:(a+b)c=ac+bc.
新课讲解
例
典例分析
计算下列各式的值:
(1) ; (2) .
(1)
(2)
解:
(加法结合律)
(分配律)
新课讲解
例
典例分析
计算(结果保留小数点后两位):
(1) ; (2) .
解:
新课讲解
练一练
1.计算.
(1)
(2)
课堂小结
1. 在实数范围内,相反数、倒数、绝对值的意义
和有理数范围内的相反数、倒数、绝对值的意
义完全一样.
3. 在进行实数的运算时,有理数的运算法则及运
算性质同样适用.
2. 实数的大小比较方法有:利用数轴比较、利用
绝对值比较、求平方比较、求差比较、求商比
较和计算近似值比较等方法.
当堂小练
1.若 a2 = 25,|b|=3,则 a + b 的所有可能值为( )
D
A.8 B.8或2 C.8或-2 D.±8或±2
当堂小练
2.计算.
拓展与延伸
要生产一种容积为 36π L 的球形容器,这种球形容器的半径是多少分米?(球的体积公式是V= πR3,其中 R 是球的半径)
解:由V= πR3 得,36π = πR3,
∴R3 = 27,
∴R = 3(dm).
答:这种球形容器的半径是 3 dm.
布置作业
请完成对应习题
6.3 实数
课时2 实数的运算
实数的性质
实数的大小比较
实数的运算(重点、难点)
学习目标
新课导入
把有理数扩充到实数之后,有理数关于相反数和绝对值的意义,大小比较以及运算法则和运算律等同样适合于实数,这节课我们就来学习这些内容.
新课讲解
知识点1 实数的性质
思考
(1) 的相反数是______,-π的相反数是______,
0的相反数是______;
(2) _______, |-π| =______, |0|= ______.
π
0
π
0
新课讲解
数a的相反数是-a,这里a表示任意一个实数.
一个正实数的绝对值是它本身;一个负实数的绝对值
是它的相反数;0的绝对值是0. 即设a表示一个实数,
则
|a|=
a,当a>0时;
0,当a=0时;
-a,当a<0时;
新课讲解
例
典例分析
(1)分别写出 , 的相反数;
(2)指出 , 分别是什么数的相反数;
(3)求 的绝对值;
(4)已知一个数的绝对值是 ,求这个数.
新课讲解
(1)因为 ,
所以 的相反数分别为 ;
(2)因为 ,
所以 分别是 的相反数;
(3)因为 ,
所以 ;
(4)因为 ,
所以绝对值为 的数是 或 .
解:
新课讲解
练一练
1.求下列各数的相反数与绝对值:
2.5, , , ,0.
2.5的相反数是-2.5,绝对值是2.5;
- 的相反数是 ,绝对值是 ;
- 的相反数是 ,绝对值是 ;
的相反数是 ,绝对值是 ;
0的相反数是0,绝对值是0.
解:
新课讲解
2.求下列各式中的实数x:
|x|= ; (2) |x|=0;
(3) |x|= ; (4) |x|=π .
(1)x=± ; (2)x=0;
(3)x=± ; (4)x=±π.
解:
新课讲解
知识点2 实数的大小比较
利用数轴比较实数的大小:对于数轴上的任意
两个点,右边的点表示的实数总比左边的点表示的
实数大.
新课讲解
例
典例分析
用“<”连接下列各数:- , ,-2 ,2.5,0.
分析:
比较一组实数的大小和比较一组有理数的大小
一样,可先求出这些数的近似数,再将这些数
在数轴上表示出来,然后根据“在数轴上右边
的点表示的数总比左边的点表示的数大”求解.
新课讲解
解:
将各数的大致位置在数轴上表示出来,如图所
示.
由图可知,各数用“<”可以连接成:-2
<- <0< <2.5.
新课讲解
练一练
1.下列四个数:-3,- ,-π,-1,其中最小的数是( )
A.-π B.-3
C.-1 D.-
A
新课讲解
知识点3 实数的运算
1.在实数范围内,进行加、减、乘、除、乘方和开方运
算时,有理数的运算法则和运算律仍然适用;实数混
合运算的运算顺序与有理数的混合运算顺序一样,先
算乘方、开方,再算乘除,最后算加减,同级运算按
照自左向右的顺序进行,有括号的先算括号里面的.
新课讲解
2. 有理数的运算律在实数范围内仍然适用,在进行
实数运算的过程中,要做到:
一“看”——看算式的结构特点,能否运用运算
律或公式;
二“用”——运用运算律或公式;
三“查”——检查过程和结果是否正确.
新课讲解
3.计算结果中若包含开方开不尽的数,则保留根号,
结果要化为最简形式.
学法指南:实数的运算律
加法交换律:a+b=b+a;
加法结合律:(a+b)+c=a+(b+c);
乘法交换律:ab=ba;
乘法结合律:(ab)c=a(bc);
乘法分配律:(a+b)c=ac+bc.
新课讲解
例
典例分析
计算下列各式的值:
(1) ; (2) .
(1)
(2)
解:
(加法结合律)
(分配律)
新课讲解
例
典例分析
计算(结果保留小数点后两位):
(1) ; (2) .
解:
新课讲解
练一练
1.计算.
(1)
(2)
课堂小结
1. 在实数范围内,相反数、倒数、绝对值的意义
和有理数范围内的相反数、倒数、绝对值的意
义完全一样.
3. 在进行实数的运算时,有理数的运算法则及运
算性质同样适用.
2. 实数的大小比较方法有:利用数轴比较、利用
绝对值比较、求平方比较、求差比较、求商比
较和计算近似值比较等方法.
当堂小练
1.若 a2 = 25,|b|=3,则 a + b 的所有可能值为( )
D
A.8 B.8或2 C.8或-2 D.±8或±2
当堂小练
2.计算.
拓展与延伸
要生产一种容积为 36π L 的球形容器,这种球形容器的半径是多少分米?(球的体积公式是V= πR3,其中 R 是球的半径)
解:由V= πR3 得,36π = πR3,
∴R3 = 27,
∴R = 3(dm).
答:这种球形容器的半径是 3 dm.
布置作业
请完成对应习题
