人教版数学七年级下册 7.2.1 用坐标表示地理位置 课件(33张)
文档属性
| 名称 | 人教版数学七年级下册 7.2.1 用坐标表示地理位置 课件(33张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 947.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 23:20:33 | ||
图片预览






文档简介
第七章 平面直角坐标系
7.2 坐标方法的简单应用
7.2.1 用坐标表示地理位置
用点的坐标表示几何图形的特征
用坐标表示地理位置
用方位角和距离表示地理位置. (重点、难点)
学习目标
新课导入
在茫茫的大海上,“北斗导航系统能对渔船进行
准确定位. ”以便及时掌握各种情况.这个系统是怎
样定位的呢,答案就在本节中.
新课讲解
知识点1 用点的坐标表示几何图形的特征
根据已知条件建立平面直角坐标系的步骤:
(1)分析条件,选择适当的点作为坐标原点;
(2)过原点在两个互相垂直的方向上分别作x轴
与y轴;
(3)确定正方向,单位长度等.
新课讲解
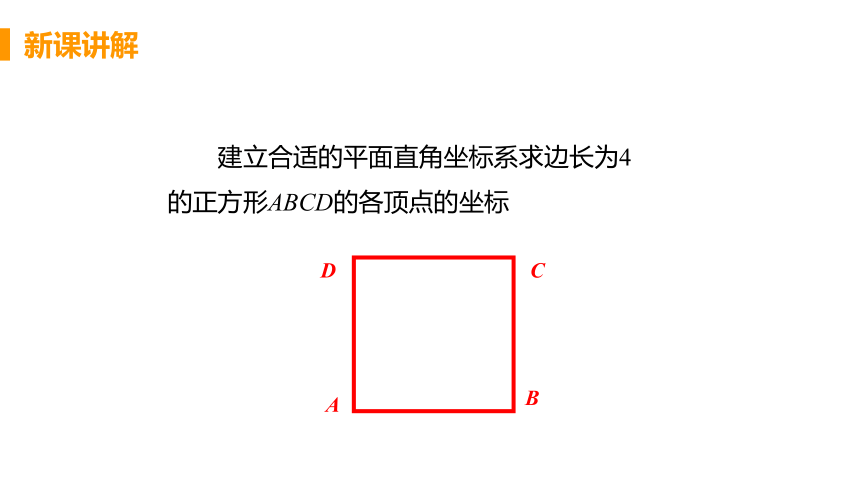
建立合适的平面直角坐标系求边长为4的正方形ABCD的各顶点的坐标
A
B
C
D
新课讲解
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
x
y
A
B
C
D
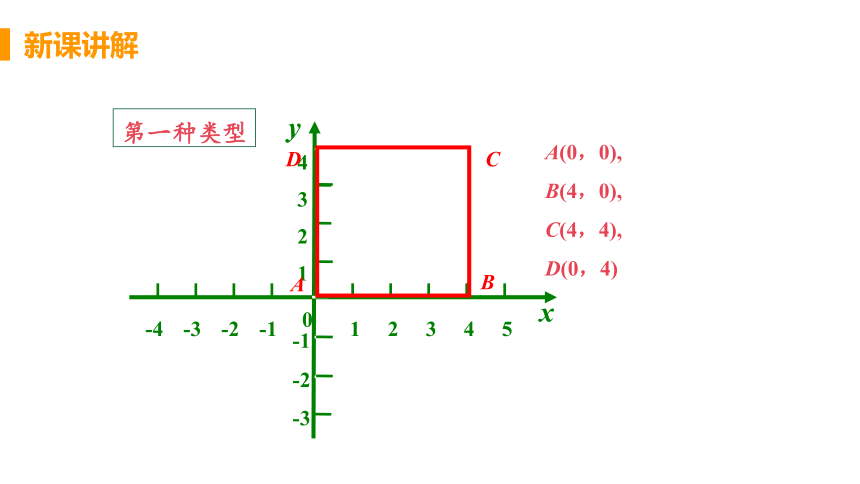
第一种类型
A(0,0), B(4,0), C(4,4),
D(0,4)
新课讲解
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
x
y
A
B
C
D
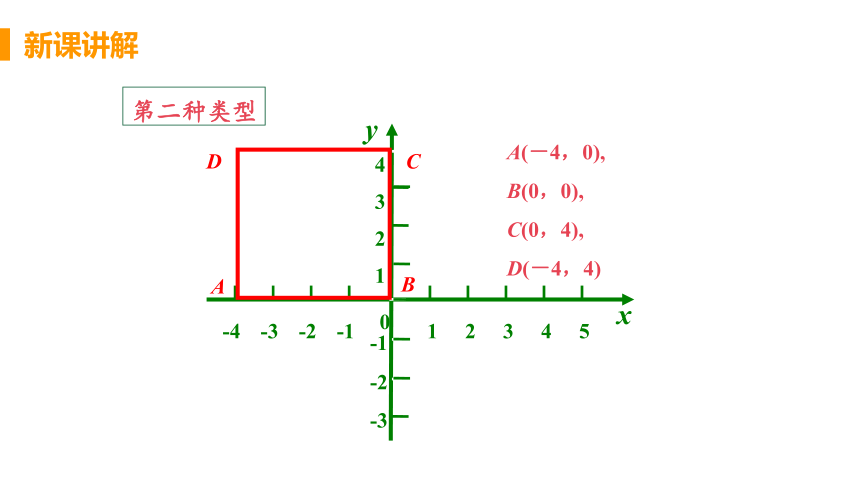
第二种类型
A(-4,0), B(0,0), C(0,4),
D(-4,4)
新课讲解
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
x
y
A
B
C
D
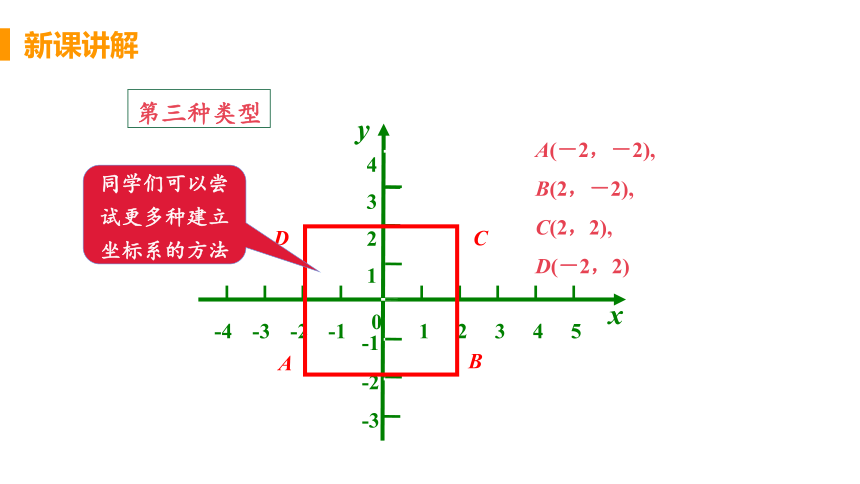
第三种类型
A(-2,-2), B(2,-2), C(2,2),
D(-2,2)
同学们可以尝试更多种建立坐标系的方法
新课讲解
可见:
(1)选取的坐标系不同,同一点的坐标不同;
(2)为使计算简化,证明方便,需要恰当地选取坐
标系;
(3)“恰当”意味着要充分利用图形的特点:垂直
关系、对称关系、平行关系、中点等。
新课讲解
例
典例分析
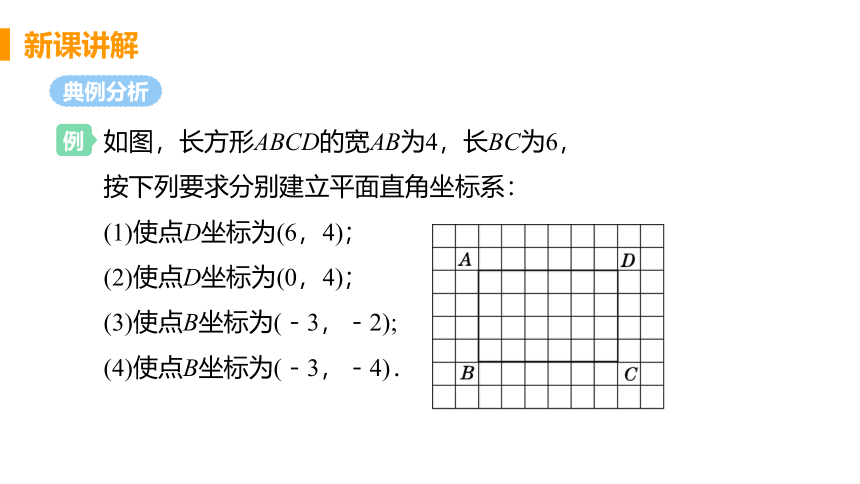
如图,长方形ABCD的宽AB为4,长BC为6,按下列要求分别建立平面直角坐标系:
(1)使点D坐标为(6,4); (2)使点D坐标为(0,4);
(3)使点B坐标为(-3,-2);
(4)使点B坐标为(-3,-4).
新课讲解
(1)先找到坐标原点,因为点D坐标为(6,4),所
以坐标原点在点D左边6个单位长度,下边4个单
位长度处,即点B;以点B为原点,BC,AB所在
直线分别为x轴和y轴,建立平面直角坐标系.
(2)(3)(4)的方法同(1).
分析:
(1)如图所示.
解:
新课讲解
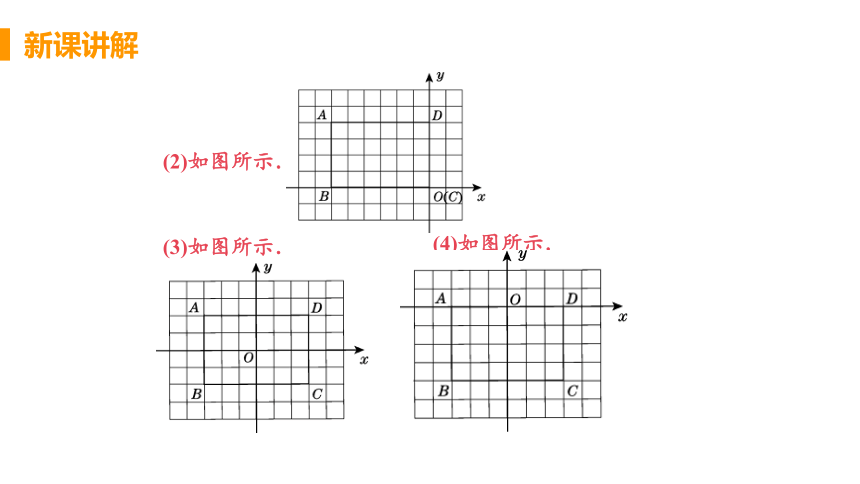
(2)如图所示.
(3)如图所示.
(4)如图所示.
新课讲解
练一练
如图,长方形ABCD的边CD在y轴上,点O为CD的中点.已知AB=4,AB交x轴于点E(-5,0),则点B的坐标为( )
A.(-5,2)
B.(2,5)
C.(5,-2)
D.(-5,-2)
B
新课讲解
知识点2 用坐标表示地理位置
思考
不管是出差办事,还
是出去旅游, 人们都愿意
带上一幅地图,它给人们
出行带来了很大方便. 如
图,这 是北京市地图的一
部分,你知道怎样 用坐标表示地理位置吗?
新课讲解
探究
根据以下条件画一幅示意图,标出学校和小刚家、
小强家、小敏家的位置.
小刚家:出校门向东走1 500 m,再向北走2 000 m.
小强家:出校门向西走2 000 m,再向北走3 500 m,
最后向东走500 m.
小敏家:出校门向南走1 000 m,再向东走3 000 m,
最后向南走750 m.
新课讲解
如图,选学校所在位置为原点,分别以正东、正北方
向为x轴、y 轴正方向建立平面直角坐标系,规定一个
单位长度代表1 m长.依题目所给条件,点(1500,2000)
就是小刚家的位置.
类似地,请你在图上画出小
强家、小敏家的位置,并标
明它们的坐标.
新课讲解
利用平面直角坐标系绘制区域内一些地点分布
情况平面图的过程如下:
(1)建立坐标系,选择一个适当的参照点为原点,确
定x轴、y轴的 正方向;
(2)根据具体问题确定单位长度;
(3)在坐标平面内画出这些点,写出各点的坐标和各
个地点的名称.
新课讲解
例
典例分析
根据下面的条件画一幅示意图,并在图中标出各个景点的位置和坐标.
菊花园:从中心广场向北走150 m,再向东走150 m;
湖心亭:从中心广场向西走150 m,再向北走100 m;
松风亭:从中心广场向西走100 m,再向南走50 m;
育德泉:从中心广场向北走200 m.
新课讲解
分析:
各个景点的位置均是以中心广场为参照点来描述
的,故选中心广场为原点,取东西方向为x轴方
向(向东为正),南北方向为y轴方向(向北为正),
建立直角坐标系,并规定一个单位长度代表50 m
长,根据行走方向和距离确定各景点的位置,标
上坐标和名称.
新课讲解
解:
如图,选中心广场所在位置为原点,分别以正东、
正北方向为x轴、y轴正方向建立平面直角坐标系,
规定一个单位长度代表50 m长.
新课讲解
练一练
长方形零件如图(单位:mm),建立适当的坐标系,用坐标表示孔心的位置.
解:
以左下角为原点,水平方向为x轴,竖直方向为y轴,建立平面直角坐标系,孔心的坐标为(15,25).
新课讲解
知识点3 用方向和距离表示地理位置
我们知道,通过建立平面直角坐标系,可以用坐
标表示平面内点的位置. 还有其他方法吗?
新课讲解
思考
如图,一艘船在A处遇险后向相距35 n mile位于B
处的救生船报警,如何用方向和距离描述救生船相对
于遇险船的位置?救生船接到报警后准备前往救援,
如何用方向和距离描述遇
险船相对于救生船的位置?
新课讲解
由图可知,救生船在遇险船北偏东60°的方向上,
与遇险船的距离是 35 n mile,用北偏东60°, 35 n
mile就可以确定救生船相对于遇险船的位置. 反过来,
用南偏西60°,35 n mile就可以确定遇险船相对于救
生船的位置.
新课讲解
方位角:从某个参照点看物体,视线与正北(或正南)方向射线的夹角称为方位角.
方位角和距离确定位置:
定义:确定平面内一个物体的位置,可以选择一
个参照物,然后用方位角和距离来表示物体的位
置,这种表示物体位置的方法称为方位角、距离
定位法.
新课讲解
例
典例分析
小明在光明广场(O点)绘制了市内的几所学校相对于光明广场的位置简图(图中1 cm表示5 km).
东方红中学在光明广场的正南方向,测得OA=1.7 cm,OB=2 cm,OC=2 cm,
OD=1.4 cm,∠AOC=
123°18′,∠AOB=68°24′,
∠AOD=88°28′. 如何确定每
个学校的具体位置?
新课讲解
分析:
要确定每个学校的位置,应以光明广场为参照物,通
过计算确定各学校所在位置的方位角,最后用方位角
和各学校到光明广场的距离来表示各学校的位置.
∠BOC=∠AOC-∠AOB=123°18′-68°24′=
54°54′;∠NOD=180°-∠AOB-∠AOD=180°
-68°24′-88°28′=23°8′.
相对于光明广场,东方国际中学在南偏东68°24′,距
离为8.5 km处;东方红中学在正南方向,距离为10 km
处;29中在南偏西54°54′,距离为10 km处;37中在
北偏东23°8′,距离为7 km处.
解:
新课讲解
练一练
如图,货轮与灯塔相距40 n mile,如何用方向和距离描述灯塔相对于货轮的位置?反过来,如何用方向和距离描述货轮相对于灯塔的位置?
灯塔在货轮的南偏东50°,距离货轮40 n mile处;货轮在灯塔北偏西50°,距离灯塔40 n mile处.
解:
课堂小结
利用平面直角坐标系表示地理位置的方法:
(1)建立平面直角坐标系,选择一个适当的参照点为原
点,确定x轴、y轴及其正方向.
(2)根据具体问题确定适当的单位长度.
(3)在坐标平面内画出这些点,写出各点的坐标和各个
地点的名称.
另外表示地理位置的方法还有:
方位角和距离定位法、网格定位法、区域定位法、经纬定位法等,不管哪种定位法,都需要两个独立的条件.
当堂小练
1.如图,已知A(-2,1),B(-6,0),若白棋A飞挂后,黑棋C尖顶,黑棋C的坐标为(______,_______).
-1 1
当堂小练
如图,是创星中学的平面示意图,其中宿舍楼暂未标注,已知宿舍楼在教学楼的北偏东约30°的方向,与教学楼实际距离约为200米,试借助刻度尺和量角器,测量图中四
点位置,能比较准确地表示
该宿舍楼位置的是( )
A.点A B.点B
C.点C D.点D
D
拓展与延伸
如图,在4×4个边长为1的正方形组成的
方格中,标有A,B两点,请建立平面直
角坐标系,用坐标表示A,B的位置.
解:
以点A为坐标原点,建立如图的平面
直角坐标系,则点A可用(0,0)表示,
点B可用(3,3)表示.
布置作业
请完成对应习题
7.2 坐标方法的简单应用
7.2.1 用坐标表示地理位置
用点的坐标表示几何图形的特征
用坐标表示地理位置
用方位角和距离表示地理位置. (重点、难点)
学习目标
新课导入
在茫茫的大海上,“北斗导航系统能对渔船进行
准确定位. ”以便及时掌握各种情况.这个系统是怎
样定位的呢,答案就在本节中.
新课讲解
知识点1 用点的坐标表示几何图形的特征
根据已知条件建立平面直角坐标系的步骤:
(1)分析条件,选择适当的点作为坐标原点;
(2)过原点在两个互相垂直的方向上分别作x轴
与y轴;
(3)确定正方向,单位长度等.
新课讲解
建立合适的平面直角坐标系求边长为4的正方形ABCD的各顶点的坐标
A
B
C
D
新课讲解
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
x
y
A
B
C
D
第一种类型
A(0,0), B(4,0), C(4,4),
D(0,4)
新课讲解
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
x
y
A
B
C
D
第二种类型
A(-4,0), B(0,0), C(0,4),
D(-4,4)
新课讲解
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
x
y
A
B
C
D
第三种类型
A(-2,-2), B(2,-2), C(2,2),
D(-2,2)
同学们可以尝试更多种建立坐标系的方法
新课讲解
可见:
(1)选取的坐标系不同,同一点的坐标不同;
(2)为使计算简化,证明方便,需要恰当地选取坐
标系;
(3)“恰当”意味着要充分利用图形的特点:垂直
关系、对称关系、平行关系、中点等。
新课讲解
例
典例分析
如图,长方形ABCD的宽AB为4,长BC为6,按下列要求分别建立平面直角坐标系:
(1)使点D坐标为(6,4); (2)使点D坐标为(0,4);
(3)使点B坐标为(-3,-2);
(4)使点B坐标为(-3,-4).
新课讲解
(1)先找到坐标原点,因为点D坐标为(6,4),所
以坐标原点在点D左边6个单位长度,下边4个单
位长度处,即点B;以点B为原点,BC,AB所在
直线分别为x轴和y轴,建立平面直角坐标系.
(2)(3)(4)的方法同(1).
分析:
(1)如图所示.
解:
新课讲解
(2)如图所示.
(3)如图所示.
(4)如图所示.
新课讲解
练一练
如图,长方形ABCD的边CD在y轴上,点O为CD的中点.已知AB=4,AB交x轴于点E(-5,0),则点B的坐标为( )
A.(-5,2)
B.(2,5)
C.(5,-2)
D.(-5,-2)
B
新课讲解
知识点2 用坐标表示地理位置
思考
不管是出差办事,还
是出去旅游, 人们都愿意
带上一幅地图,它给人们
出行带来了很大方便. 如
图,这 是北京市地图的一
部分,你知道怎样 用坐标表示地理位置吗?
新课讲解
探究
根据以下条件画一幅示意图,标出学校和小刚家、
小强家、小敏家的位置.
小刚家:出校门向东走1 500 m,再向北走2 000 m.
小强家:出校门向西走2 000 m,再向北走3 500 m,
最后向东走500 m.
小敏家:出校门向南走1 000 m,再向东走3 000 m,
最后向南走750 m.
新课讲解
如图,选学校所在位置为原点,分别以正东、正北方
向为x轴、y 轴正方向建立平面直角坐标系,规定一个
单位长度代表1 m长.依题目所给条件,点(1500,2000)
就是小刚家的位置.
类似地,请你在图上画出小
强家、小敏家的位置,并标
明它们的坐标.
新课讲解
利用平面直角坐标系绘制区域内一些地点分布
情况平面图的过程如下:
(1)建立坐标系,选择一个适当的参照点为原点,确
定x轴、y轴的 正方向;
(2)根据具体问题确定单位长度;
(3)在坐标平面内画出这些点,写出各点的坐标和各
个地点的名称.
新课讲解
例
典例分析
根据下面的条件画一幅示意图,并在图中标出各个景点的位置和坐标.
菊花园:从中心广场向北走150 m,再向东走150 m;
湖心亭:从中心广场向西走150 m,再向北走100 m;
松风亭:从中心广场向西走100 m,再向南走50 m;
育德泉:从中心广场向北走200 m.
新课讲解
分析:
各个景点的位置均是以中心广场为参照点来描述
的,故选中心广场为原点,取东西方向为x轴方
向(向东为正),南北方向为y轴方向(向北为正),
建立直角坐标系,并规定一个单位长度代表50 m
长,根据行走方向和距离确定各景点的位置,标
上坐标和名称.
新课讲解
解:
如图,选中心广场所在位置为原点,分别以正东、
正北方向为x轴、y轴正方向建立平面直角坐标系,
规定一个单位长度代表50 m长.
新课讲解
练一练
长方形零件如图(单位:mm),建立适当的坐标系,用坐标表示孔心的位置.
解:
以左下角为原点,水平方向为x轴,竖直方向为y轴,建立平面直角坐标系,孔心的坐标为(15,25).
新课讲解
知识点3 用方向和距离表示地理位置
我们知道,通过建立平面直角坐标系,可以用坐
标表示平面内点的位置. 还有其他方法吗?
新课讲解
思考
如图,一艘船在A处遇险后向相距35 n mile位于B
处的救生船报警,如何用方向和距离描述救生船相对
于遇险船的位置?救生船接到报警后准备前往救援,
如何用方向和距离描述遇
险船相对于救生船的位置?
新课讲解
由图可知,救生船在遇险船北偏东60°的方向上,
与遇险船的距离是 35 n mile,用北偏东60°, 35 n
mile就可以确定救生船相对于遇险船的位置. 反过来,
用南偏西60°,35 n mile就可以确定遇险船相对于救
生船的位置.
新课讲解
方位角:从某个参照点看物体,视线与正北(或正南)方向射线的夹角称为方位角.
方位角和距离确定位置:
定义:确定平面内一个物体的位置,可以选择一
个参照物,然后用方位角和距离来表示物体的位
置,这种表示物体位置的方法称为方位角、距离
定位法.
新课讲解
例
典例分析
小明在光明广场(O点)绘制了市内的几所学校相对于光明广场的位置简图(图中1 cm表示5 km).
东方红中学在光明广场的正南方向,测得OA=1.7 cm,OB=2 cm,OC=2 cm,
OD=1.4 cm,∠AOC=
123°18′,∠AOB=68°24′,
∠AOD=88°28′. 如何确定每
个学校的具体位置?
新课讲解
分析:
要确定每个学校的位置,应以光明广场为参照物,通
过计算确定各学校所在位置的方位角,最后用方位角
和各学校到光明广场的距离来表示各学校的位置.
∠BOC=∠AOC-∠AOB=123°18′-68°24′=
54°54′;∠NOD=180°-∠AOB-∠AOD=180°
-68°24′-88°28′=23°8′.
相对于光明广场,东方国际中学在南偏东68°24′,距
离为8.5 km处;东方红中学在正南方向,距离为10 km
处;29中在南偏西54°54′,距离为10 km处;37中在
北偏东23°8′,距离为7 km处.
解:
新课讲解
练一练
如图,货轮与灯塔相距40 n mile,如何用方向和距离描述灯塔相对于货轮的位置?反过来,如何用方向和距离描述货轮相对于灯塔的位置?
灯塔在货轮的南偏东50°,距离货轮40 n mile处;货轮在灯塔北偏西50°,距离灯塔40 n mile处.
解:
课堂小结
利用平面直角坐标系表示地理位置的方法:
(1)建立平面直角坐标系,选择一个适当的参照点为原
点,确定x轴、y轴及其正方向.
(2)根据具体问题确定适当的单位长度.
(3)在坐标平面内画出这些点,写出各点的坐标和各个
地点的名称.
另外表示地理位置的方法还有:
方位角和距离定位法、网格定位法、区域定位法、经纬定位法等,不管哪种定位法,都需要两个独立的条件.
当堂小练
1.如图,已知A(-2,1),B(-6,0),若白棋A飞挂后,黑棋C尖顶,黑棋C的坐标为(______,_______).
-1 1
当堂小练
如图,是创星中学的平面示意图,其中宿舍楼暂未标注,已知宿舍楼在教学楼的北偏东约30°的方向,与教学楼实际距离约为200米,试借助刻度尺和量角器,测量图中四
点位置,能比较准确地表示
该宿舍楼位置的是( )
A.点A B.点B
C.点C D.点D
D
拓展与延伸
如图,在4×4个边长为1的正方形组成的
方格中,标有A,B两点,请建立平面直
角坐标系,用坐标表示A,B的位置.
解:
以点A为坐标原点,建立如图的平面
直角坐标系,则点A可用(0,0)表示,
点B可用(3,3)表示.
布置作业
请完成对应习题
