人教版八年级数学上册15.2_分式的化简求值同步习题(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学上册15.2_分式的化简求值同步习题(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 22.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 00:32:10 | ||
图片预览


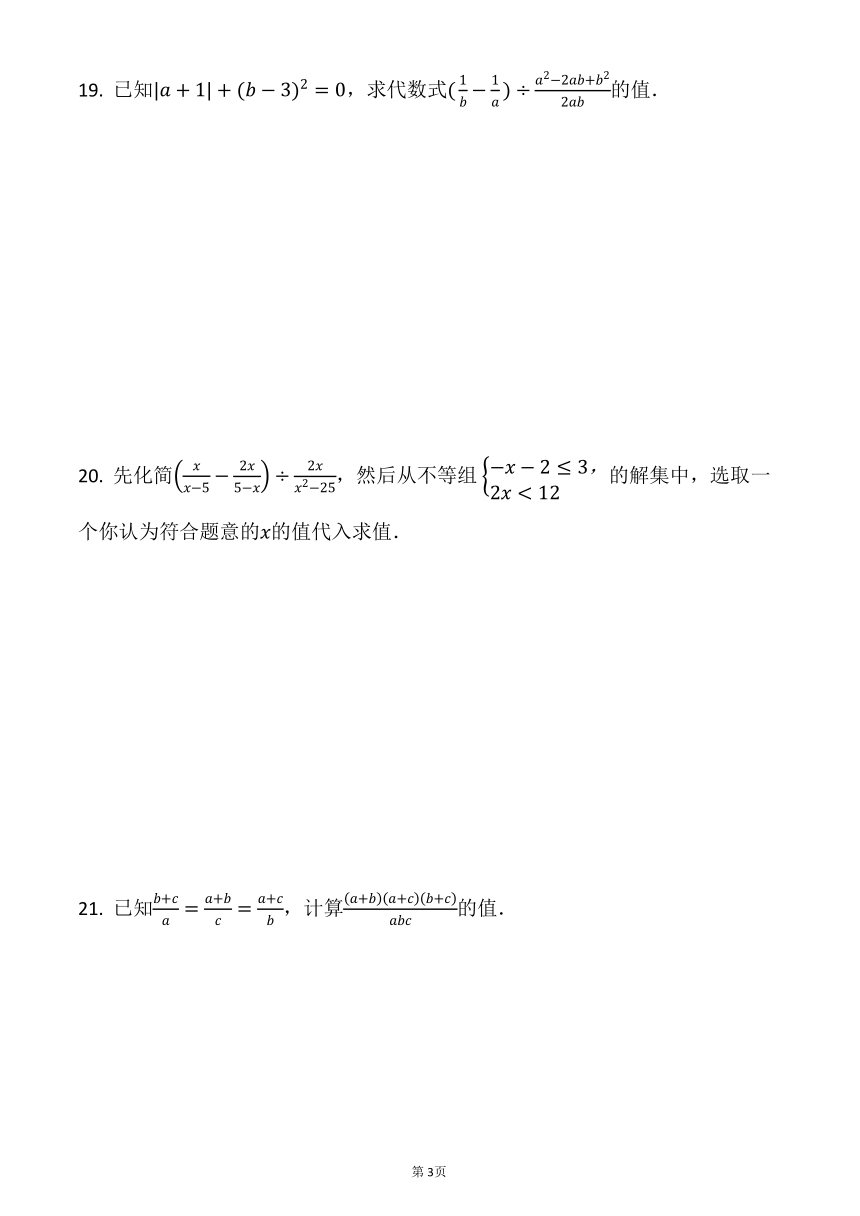
文档简介
15.2
分式的化简求值
1.
已知,则的值为(?
?
?
?)
A.
B.
C.
D.
2.
已知,则的值为(?
?
?
?
)
A.
B.
C.
D.
3.
下列各式中正确的是(?
?
?
?
)
A.
B.
C.
D.
4.
在等式中,为(?
?
?
?
)
A.
B.
C.
D.
5.
若,则的值为(?
?
?
?
)
A.
B.
C.
D.
6.
已知,则的值等于(?
?
?
?
)
A.
B.
C.
D.
7.
已知,则分式的值是(?
?
?
?
)
A.
B.
C.
D.
8.
若,则(????????)
A.
B.
C.
D.
9.
若,则的值是?
?
?
?
A.
B.
C.
D.
10.
下列计算不正确的是(?
?
?
?
)
A.
B.
C.
D.
11.
若化简的结果为,则“”是(????????)
A.
B.
C.
D.
12.
有一道化简求值题:先化简,再选你喜欢的一个数代入求值.在解答此题时,甲、乙、丙、丁四位同学分别把代入,求得的结果分别是、、、,四位同学中计算正确的是(????????)
A.甲
B.乙
C.丙
D.丁
13.
当________时,分式的值为零.
14.
已知,则的值是________.
15.
已知,则代数式的值为________.
16.
已知,=,则的值为________.
17.
先化简,再求值:
,其中.
18.
先化简,再求值:,其中为整数,且满足.
19.
已知,求代数式的值.
?
20.
先化简,然后从不等组
的解集中,选取一个你认为符合题意的的值代入求值.
?
21.
已知,计算的值.
?
22.
阅读材料并解答以下问题,我们知道,假分数可以化为带分数.例如:
.在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如:
,,这样的分式就是假分式;,这样的分式就是真分式.类似的,假分式也可以化为带分式(即:整式与真分式和的形式).
例如:;
.
将分式化为带分式;
若分式的值为整数,求的整数值;
当________时,
有最小值,求出这个最小值.
参考答案与试题解析
15.2
分式的化简求值
一、
选择题
1.【答案】B
2.【答案】B
3.【答案】B
4.【答案】A
5.【答案】D
6.【答案】A
7.【答案】A
8.【答案】B
9.【答案】C
10.【答案】C
11.【答案】D
12.【答案】D
二、
填空题
13.【答案】略
14.【答案】
15.【答案】
16.【答案】
三、
解答题
17.【答案】
解:
,
当时,
原式.
18.【答案】
解:原式
.
∵
,且为整数,
∴
或.
∵
,∴
,
∴
当时,原式.
19.【答案】
解:∵
,
∴
,,解得,.
原式
,
当,时,原式.
20.【答案】
解:原式,
不等式组?
解①得:
,
解②得:
,
所以原不等式组的解集为:,
根据原式分母不为零,可知:且且,
所以取代入得:原式.
21.【答案】
解:设,,,
三个等式相加得,
所以有:?或,
即或,
所以的值为:或.
22.【答案】
解:原式.
,
要使为整数且的值也为整数,则必为整数,
∴
为的因数,
∴
或,
解得:,,,.
.
第6页
第7页
分式的化简求值
1.
已知,则的值为(?
?
?
?)
A.
B.
C.
D.
2.
已知,则的值为(?
?
?
?
)
A.
B.
C.
D.
3.
下列各式中正确的是(?
?
?
?
)
A.
B.
C.
D.
4.
在等式中,为(?
?
?
?
)
A.
B.
C.
D.
5.
若,则的值为(?
?
?
?
)
A.
B.
C.
D.
6.
已知,则的值等于(?
?
?
?
)
A.
B.
C.
D.
7.
已知,则分式的值是(?
?
?
?
)
A.
B.
C.
D.
8.
若,则(????????)
A.
B.
C.
D.
9.
若,则的值是?
?
?
?
A.
B.
C.
D.
10.
下列计算不正确的是(?
?
?
?
)
A.
B.
C.
D.
11.
若化简的结果为,则“”是(????????)
A.
B.
C.
D.
12.
有一道化简求值题:先化简,再选你喜欢的一个数代入求值.在解答此题时,甲、乙、丙、丁四位同学分别把代入,求得的结果分别是、、、,四位同学中计算正确的是(????????)
A.甲
B.乙
C.丙
D.丁
13.
当________时,分式的值为零.
14.
已知,则的值是________.
15.
已知,则代数式的值为________.
16.
已知,=,则的值为________.
17.
先化简,再求值:
,其中.
18.
先化简,再求值:,其中为整数,且满足.
19.
已知,求代数式的值.
?
20.
先化简,然后从不等组
的解集中,选取一个你认为符合题意的的值代入求值.
?
21.
已知,计算的值.
?
22.
阅读材料并解答以下问题,我们知道,假分数可以化为带分数.例如:
.在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如:
,,这样的分式就是假分式;,这样的分式就是真分式.类似的,假分式也可以化为带分式(即:整式与真分式和的形式).
例如:;
.
将分式化为带分式;
若分式的值为整数,求的整数值;
当________时,
有最小值,求出这个最小值.
参考答案与试题解析
15.2
分式的化简求值
一、
选择题
1.【答案】B
2.【答案】B
3.【答案】B
4.【答案】A
5.【答案】D
6.【答案】A
7.【答案】A
8.【答案】B
9.【答案】C
10.【答案】C
11.【答案】D
12.【答案】D
二、
填空题
13.【答案】略
14.【答案】
15.【答案】
16.【答案】
三、
解答题
17.【答案】
解:
,
当时,
原式.
18.【答案】
解:原式
.
∵
,且为整数,
∴
或.
∵
,∴
,
∴
当时,原式.
19.【答案】
解:∵
,
∴
,,解得,.
原式
,
当,时,原式.
20.【答案】
解:原式,
不等式组?
解①得:
,
解②得:
,
所以原不等式组的解集为:,
根据原式分母不为零,可知:且且,
所以取代入得:原式.
21.【答案】
解:设,,,
三个等式相加得,
所以有:?或,
即或,
所以的值为:或.
22.【答案】
解:原式.
,
要使为整数且的值也为整数,则必为整数,
∴
为的因数,
∴
或,
解得:,,,.
.
第6页
第7页
