人教版七年级数学下5.1.1相交线同步训练(Word版 含答案)
文档属性
| 名称 | 人教版七年级数学下5.1.1相交线同步训练(Word版 含答案) | 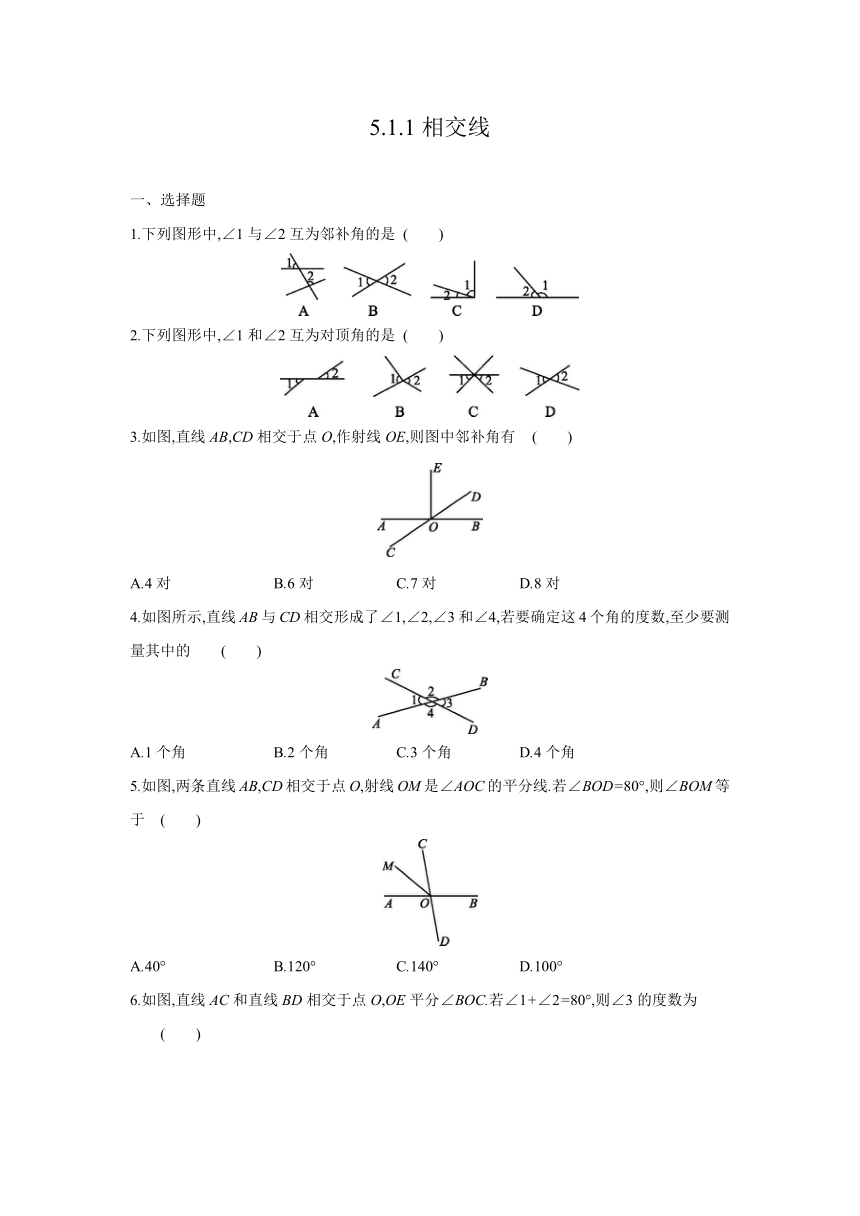 | |
| 格式 | docx | ||
| 文件大小 | 176.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 00:34:35 | ||
图片预览



文档简介
5.1.1相交线
一、选择题
1.下列图形中,∠1与∠2互为邻补角的是
( )
2.下列图形中,∠1和∠2互为对顶角的是
( )
3.如图,直线AB,CD相交于点O,作射线OE,则图中邻补角有
( )
A.4对
B.6对
C.7对
D.8对
4.如图所示,直线AB与CD相交形成了∠1,∠2,∠3和∠4,若要确定这4个角的度数,至少要测量其中的
( )
A.1个角
B.2个角
C.3个角
D.4个角
5.如图,两条直线AB,CD相交于点O,射线OM是∠AOC的平分线.若∠BOD=80°,则∠BOM等于
( )
A.40°
B.120°
C.140°
D.100°
6.如图,直线AC和直线BD相交于点O,OE平分∠BOC.若∠1+∠2=80°,则∠3的度数为
( )
A.40°
B.50°
C.60°
D.70°
二、填空题
7.如图,直线AB,CD,EF相交于点O,则∠BOE的对顶角是 ,∠COE的邻补角是 ,∠COG的邻补角是 .?
8.如图,三条直线相交于一点,则∠1+∠2+∠3= °.?
9.如图所示,直线AB,CD,EF相交于点O.若∠1=20°,∠BOC=80°,则∠2= °.?
10.如图,直线AB,CD相交于点O,OE平分∠AOD.若∠BOD=110°,则∠AOE= °.?
11.如图,直线AB,CD相交于点O,∠AOE=90°,则∠AOC-∠BOD= °,∠AOC+
∠AOD= °,∠AOC+∠DOE= °.?
三、解答题
12.如图,直线AB,CD,EF相交于点O.
(1)写出∠COE的邻补角;
(2)分别写出∠COE和∠BOE的对顶角;
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF和∠FOC的度数.
13.如图,直线AB,CD相交于点O,∠1-∠2=85°,求∠AOC的度数.
14.如图,直线AB,CD相交于点O,OE平分∠AOC,∠EOA∶∠AOD=1∶4,求∠EOB的度数.
15.如图,直线AB,CD相交于点O,∠DOE=∠BOD,OF平分∠AOE,∠BOD=20°.
(1)求∠AOE的度数;
(2)求∠COF的度数.
16.如图,直线AB,CD相交于点O,OE平分∠AOD.
(1)若∠AOC=46°,求∠BOE的度数;
(2)若∠AOC=x°,求∠BOE的度数.
17.下列各图中,直线都交于一点,请探究交于一点的直线的条数与所形成的对顶角(不含平角)的对数之间的规律.
(1)请观察上图并填写下表;
交于一点的直线的条数
2
3
4
对顶角的对数
?
?
?
(2)若n条直线交于一点,则共有 对对顶角(用含n的式子表示);?
(3)当100条直线交于一点时,共有 对对顶角.?
参考答案
1.D 2.D
3.B 解析:
邻补角有∠AOC与∠AOD,∠AOC与∠COB,∠BOD与∠AOD,∠BOD与∠COB,∠EOA与∠EOB,∠EOD与∠EOC,共6对.故选B.
4.A 解析:
根据题意,可得∠1=∠3,∠2=∠4,且∠1+∠2=∠3+∠4=180°,所以要确定这4个角的度数,至少要测量其中的1个角.故选A.
5.C 解析:
因为∠BOD=80°,所以∠AOC=80°,∠COB=100°.因为射线OM是∠AOC的平分线,所以∠COM=40°,所以∠BOM=40°+100°=140°.
6.D 解析:
因为∠1=∠2,∠1+∠2=80°,所以∠1=∠2=40°,所以∠BOC=140°.因为OE平分∠BOC,所以∠3=70°.故选D.
7.∠AOF ∠COF和∠DOE ∠DOG
8.180 9.60 10.35 11.0 180 90
12.解:(1)∠COE的邻补角为∠COF和∠EOD.
(2)∠COE和∠BOE的对顶角分别为∠DOF和∠AOF.
(3)因为∠BOF=90°,由邻补角的定义可得∠AOF=90°.
又因为∠AOC=∠BOD=60°,
所以∠FOC=∠AOF+∠AOC=90°+60°=150°.
13.解析:
利用邻补角和对顶角的性质计算.
解:因为∠1-∠2=85°,所以∠1=∠2+85°.因为∠1+∠2=180°,所以∠2+85°+∠2=180°,所以2∠2=95°,所以∠2=47.5°.故∠AOC=∠2=47.5°.
14.解:设∠EOA=x.因为OE平分∠AOC,
所以∠AOC=2x.
因为∠EOA∶∠AOD=1∶4,
所以∠AOD=4x.
因为∠AOC+∠AOD=180°,
所以2x+4x=180°,解得x=30°,
所以∠EOB=180°-30°=150°.
故∠EOB的度数是150°.
15.解:(1)因为∠BOD=20°,∠DOE=∠BOD,
所以∠BOE=20°+20°=40°,
所以∠AOE=180°-40°=140°.
(2)因为OF平分∠AOE,所以∠EOF=∠AOE=×140°=70°.又因为∠DOE=20°,所以
∠COF=180°-20°-70°=90°.
16.解:(1)因为∠AOC=46°,
所以∠AOD=180°-∠AOC=180°-46°=134°.
因为OE平分∠AOD,
所以∠DOE=∠AOD=×134°=67°.
因为∠BOD=∠AOC=46°,
所以∠BOE=∠DOE+∠BOD=67°+46°=113°.
(2)因为∠AOC=x°,
所以∠AOD=180°-∠AOC=(180-x)°.
因为OE平分∠AOD,
所以∠DOE=∠AOD=(180-x)°=90-x°.
因为∠BOD=∠AOC=x°,
所以∠BOE=∠DOE+∠BOD=90-x°+x°=°.
17.(1)2 6 12 (2)n(n-1) (3)9900
一、选择题
1.下列图形中,∠1与∠2互为邻补角的是
( )
2.下列图形中,∠1和∠2互为对顶角的是
( )
3.如图,直线AB,CD相交于点O,作射线OE,则图中邻补角有
( )
A.4对
B.6对
C.7对
D.8对
4.如图所示,直线AB与CD相交形成了∠1,∠2,∠3和∠4,若要确定这4个角的度数,至少要测量其中的
( )
A.1个角
B.2个角
C.3个角
D.4个角
5.如图,两条直线AB,CD相交于点O,射线OM是∠AOC的平分线.若∠BOD=80°,则∠BOM等于
( )
A.40°
B.120°
C.140°
D.100°
6.如图,直线AC和直线BD相交于点O,OE平分∠BOC.若∠1+∠2=80°,则∠3的度数为
( )
A.40°
B.50°
C.60°
D.70°
二、填空题
7.如图,直线AB,CD,EF相交于点O,则∠BOE的对顶角是 ,∠COE的邻补角是 ,∠COG的邻补角是 .?
8.如图,三条直线相交于一点,则∠1+∠2+∠3= °.?
9.如图所示,直线AB,CD,EF相交于点O.若∠1=20°,∠BOC=80°,则∠2= °.?
10.如图,直线AB,CD相交于点O,OE平分∠AOD.若∠BOD=110°,则∠AOE= °.?
11.如图,直线AB,CD相交于点O,∠AOE=90°,则∠AOC-∠BOD= °,∠AOC+
∠AOD= °,∠AOC+∠DOE= °.?
三、解答题
12.如图,直线AB,CD,EF相交于点O.
(1)写出∠COE的邻补角;
(2)分别写出∠COE和∠BOE的对顶角;
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF和∠FOC的度数.
13.如图,直线AB,CD相交于点O,∠1-∠2=85°,求∠AOC的度数.
14.如图,直线AB,CD相交于点O,OE平分∠AOC,∠EOA∶∠AOD=1∶4,求∠EOB的度数.
15.如图,直线AB,CD相交于点O,∠DOE=∠BOD,OF平分∠AOE,∠BOD=20°.
(1)求∠AOE的度数;
(2)求∠COF的度数.
16.如图,直线AB,CD相交于点O,OE平分∠AOD.
(1)若∠AOC=46°,求∠BOE的度数;
(2)若∠AOC=x°,求∠BOE的度数.
17.下列各图中,直线都交于一点,请探究交于一点的直线的条数与所形成的对顶角(不含平角)的对数之间的规律.
(1)请观察上图并填写下表;
交于一点的直线的条数
2
3
4
对顶角的对数
?
?
?
(2)若n条直线交于一点,则共有 对对顶角(用含n的式子表示);?
(3)当100条直线交于一点时,共有 对对顶角.?
参考答案
1.D 2.D
3.B 解析:
邻补角有∠AOC与∠AOD,∠AOC与∠COB,∠BOD与∠AOD,∠BOD与∠COB,∠EOA与∠EOB,∠EOD与∠EOC,共6对.故选B.
4.A 解析:
根据题意,可得∠1=∠3,∠2=∠4,且∠1+∠2=∠3+∠4=180°,所以要确定这4个角的度数,至少要测量其中的1个角.故选A.
5.C 解析:
因为∠BOD=80°,所以∠AOC=80°,∠COB=100°.因为射线OM是∠AOC的平分线,所以∠COM=40°,所以∠BOM=40°+100°=140°.
6.D 解析:
因为∠1=∠2,∠1+∠2=80°,所以∠1=∠2=40°,所以∠BOC=140°.因为OE平分∠BOC,所以∠3=70°.故选D.
7.∠AOF ∠COF和∠DOE ∠DOG
8.180 9.60 10.35 11.0 180 90
12.解:(1)∠COE的邻补角为∠COF和∠EOD.
(2)∠COE和∠BOE的对顶角分别为∠DOF和∠AOF.
(3)因为∠BOF=90°,由邻补角的定义可得∠AOF=90°.
又因为∠AOC=∠BOD=60°,
所以∠FOC=∠AOF+∠AOC=90°+60°=150°.
13.解析:
利用邻补角和对顶角的性质计算.
解:因为∠1-∠2=85°,所以∠1=∠2+85°.因为∠1+∠2=180°,所以∠2+85°+∠2=180°,所以2∠2=95°,所以∠2=47.5°.故∠AOC=∠2=47.5°.
14.解:设∠EOA=x.因为OE平分∠AOC,
所以∠AOC=2x.
因为∠EOA∶∠AOD=1∶4,
所以∠AOD=4x.
因为∠AOC+∠AOD=180°,
所以2x+4x=180°,解得x=30°,
所以∠EOB=180°-30°=150°.
故∠EOB的度数是150°.
15.解:(1)因为∠BOD=20°,∠DOE=∠BOD,
所以∠BOE=20°+20°=40°,
所以∠AOE=180°-40°=140°.
(2)因为OF平分∠AOE,所以∠EOF=∠AOE=×140°=70°.又因为∠DOE=20°,所以
∠COF=180°-20°-70°=90°.
16.解:(1)因为∠AOC=46°,
所以∠AOD=180°-∠AOC=180°-46°=134°.
因为OE平分∠AOD,
所以∠DOE=∠AOD=×134°=67°.
因为∠BOD=∠AOC=46°,
所以∠BOE=∠DOE+∠BOD=67°+46°=113°.
(2)因为∠AOC=x°,
所以∠AOD=180°-∠AOC=(180-x)°.
因为OE平分∠AOD,
所以∠DOE=∠AOD=(180-x)°=90-x°.
因为∠BOD=∠AOC=x°,
所以∠BOE=∠DOE+∠BOD=90-x°+x°=°.
17.(1)2 6 12 (2)n(n-1) (3)9900
