人教版七年级下册数学 5.1:相交线 同步练习 (Word版 含解析)
文档属性
| 名称 | 人教版七年级下册数学 5.1:相交线 同步练习 (Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 119.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 00:33:41 | ||
图片预览




文档简介
5.1相交线 同步练习
一.选择题
1.下列各图中,∠1与∠2是对顶角的是( )
A. B.
C. D.
2.如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )
A.A点 B.B点 C.C点 D.D点
3.如图,下列结论中错误的是( )
A.∠1与∠2是同旁内角 B.∠1与∠4是内错角
C.∠5与∠6是内错角 D.∠3与∠5是同位角
4.如图,AB和CD相交于点O,则下列结论正确的是( )
A.∠1>∠2 B.∠2=∠3 C.∠1=∠4+∠5 D.∠2<∠5
5.如图,AC⊥BC,CD⊥AB,下列结论中,正确的结论有( )
①线段CD的长度是C点到AB的距离;
②线段AC的长度是A点到BC的距离;
③AB>AC>CD.
A.0个 B.1个 C.2个 D.3个
6.如图,给出以下说法:①∠B和∠1是同旁内角;②∠3和∠4是内错角;③∠B和∠AEC是同位角;④∠A和∠3是内错角;⑤∠2和∠3是对顶角,其中正确的个数是( )
A.4个 B.3个 C.2个 D.1个
7.如图所示,下列说法:
①∠1与∠C是同位角;
②∠2与∠C是内错角;
③∠3与∠B是同旁内角;
④∠3与∠C是同旁内角.
其中正确的是( )
A.①②③ B.②③④ C.①③④ D.①②④
8.如图,给出下列说法:①∠A和∠4是同位角;②∠1和∠3是对顶角;③∠2和∠4是内错角;④∠A和∠BCD是同旁内角.其中说法错误的有( )
A.1个 B.2个 C.3个 D.4个
9.如图,直线AB、CD与EF相交,则∠2的内错角是( )
A.∠8 B.∠7 C.∠6 D.∠4
10.观察如图,并阅读图形下面的相关文字:
两条直线相交,最多有1个交点;三条直线相交,最多有3个交点;4条直线相交,最多有6个交点……
像这样,20条直线相交,交点最多的个数是( )
A.100个 B.135个 C.190个 D.200个
二.填空题(共5小题)
11.已知线段AB与直线CD互相垂直,垂足为点O,且AO=5cm,BO=3cm,则线段AB的长为 .
12.如图,∠1和∠3是直线 和 被直线 所截而成的 角;图中与∠2是同旁内角的角有 个.
13.已知:直线AB与直线CD交于点O,∠BOC=45°,
(1)如图,若EO⊥AB,则∠DOE= .
(2)如图,若EO平分∠AOC,则∠DOE= .
14.如图,直线AB,CD相交于O,OE⊥AB,O为垂足,∠COE=34°,则∠BOD= 度.
15.如图①两条直线交于一点,图中共有=2对对顶角;如图②三条直线交于一点,图中共有=6对对顶角;如图③四条直线交于一点,图中共有=12对对顶角;…;按这样的规律,六条直线交于一点,那么图中共有 对对顶角.(只填数字)
三.解答题
16.如图,两条直线a,b相交.
(1)如果∠1=50°,求∠2,∠3的度数;
(2)如果∠2=3∠1,求∠3,∠4的度数.
17.如图,直线AB,CD交于点O,OE平分∠COB,OF是∠EOD的角平分线.
(1)说明:∠AOD=2∠COE;
(2)若∠AOC=50°,求∠EOF的度数;
(3)若∠BOF=15°,求∠AOC的度数.
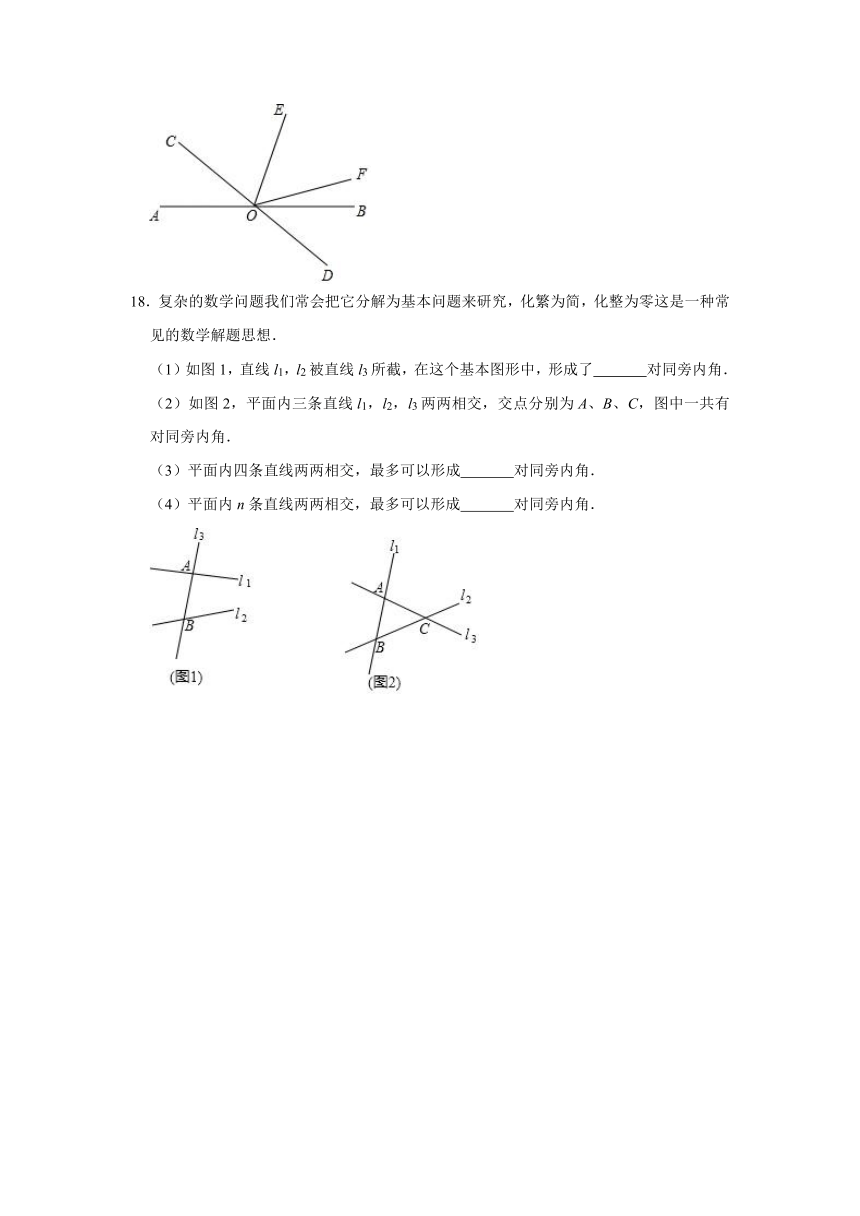
18.复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想.
(1)如图1,直线l1,l2被直线l3所截,在这个基本图形中,形成了 对同旁内角.
(2)如图2,平面内三条直线l1,l2,l3两两相交,交点分别为A、B、C,图中一共有 对同旁内角.
(3)平面内四条直线两两相交,最多可以形成 对同旁内角.
(4)平面内n条直线两两相交,最多可以形成 对同旁内角.
参考答案
一.选择题
1.解:A、∠1与∠2不是对顶角;
B、∠1与∠2不是对顶角;
C、∠1与∠2不是对顶角;
D、∠1与∠2是对顶角;
故选:D.
2.解:根据垂线段最短可得:应建在A处,
故选:A.
3.解:如图,∠1与∠2是直线a与直线b被直线c所截的同旁内角,因此选项A不符合题意;
∠1与∠6是直线a与直线b被直线c所截的内错角,而∠6与∠4是邻补角,所以∠1与∠4不是内错角,因此选项B符合题意;
∠5与∠6是直线c与直线d被直线b所截的内错角,因此选项C不符合题意;
∠3与∠5是直线c与直线d被直线b所截的同位角,因此选项D不符合题意;
故选:B.
4.解:A.∵∠1与∠2是对顶角,
∴∠1=∠2,
故本选项不符合题意;
B.∵∠2是△AOD的外角,
∴∠2>∠3,
故本选项不符合题意;
C.∵∠1是△OBC的外角,
∴∠1=∠4+∠5,
故本选项符合题意;
D.∵∠2是△OBC的外角,
∴∠2>∠5,
故本选项不符合题意;
故选:C.
5.解:①线段CD的长度是C点到AB的距离,故结论正确;
②应该是线段AC的长度是A点到BC的距离,故结论正确;
③在同一直角三角形中,斜边大于直角边,所以AB>AC>CD,故结论正确;
故选:D.
6.解:∠B和∠1是直线AB和CE被直线BC所截的一对同旁内角,故①正确;
∠3和∠4不是内错角,故②错误;
∠B和∠AEC是直线CE和BC被直线AB所截的一对同位角,故③正确;
∠A和∠3是直线AB和CD被直线AC所截的一对内错角,故④正确;
∠2和∠3不是对顶角,故⑤错误;
即正确的有3个,
故选:B.
7.解:①∠1与∠C是同位角,说法正确;
②∠2与∠C是内错角,说法错误;
③∠3与∠B是同旁内角,说法正确;
④∠3与∠C是同旁内角,说法正确;
故选:C.
8.解:①∠A和∠4是同位角,说法正确;
②∠1和∠3是对顶角,说法错误;
③∠2和∠4是内错角,说法正确;
④∠A和∠BCD是同旁内角说法错误;
说法错误的有2个,
故选:B.
9.解:由题可得,∠2的内错角是∠7,
故选:B.
10.解:2条直线相交最多有1个交点,1=×1×2,
3条直线相交最多有3个交点,3=1+2=×2×3,
4条直线相交最多有6个交点,6=1+2+3=×3×4,
5条直线相交最多有10个交点,10=1+2+3+4=×4×5,
…
n条直线相交最多有交点的个数是:n(n﹣1).
20条直线相交最多有交点的个数是:n(n﹣1)=×20×19=190.
故选:C.
二.填空题(共5小题)
11.解:当点O在线段AB内时,AB=AO+BO=5cm+3cm=8cm,
当点O在线段AB外时,AB=AO﹣BO=5cm﹣3cm=2cm.
故答案为:8cm 或2cm.
12.解:∠1和∠3是直线AB和AC被直线DE所截而成的内错角;图中与∠2 是同旁内角的角有∠6、∠5、∠7,共3个,
故答案为:AB、AC、DE、内错,3.
13.解:(1)∵直线AB与直线CD相交,
∴∠AOD=∠BOC=45°.
∵EO⊥AB,
∴∠AOE=90°,
∴∠DOE=∠AOD+∠AOE=135°;
(2)∵直线AB与直线CD相交,
∴∠AOD=∠BOC=45°,∠AOC=135°,
∵EO平分∠AOC,
∴∠AOE=∠AOC=67.5°,
∴∠DOE=∠AOD+∠AOE=112.5°.
故答案为:135°;112.5°.
14.解:∵OE⊥AB,∠COE=34°,
∴∠BOD=90°﹣∠COE=90°﹣34°=56°.
故答案为:56.
15.解:由各图形直线的条数,以及计算对顶角个数的式子,可知
6条直线相交时,这个图形的对顶角的个数是:=30对对顶角.
三.解答题
16.解:(1)∵∠1=50°,∠1+∠2=180°,
∴∠2=180°﹣50°=130°,
又∵∠3与∠1是对顶角,
∴∠3=∠1=50°;
(2)∵∠2=3∠1,∠1+∠2=180°,
∴∠1+3∠1=180°,
∴4∠1=180°,
∴∠1=45°,
∴∠3=∠1=45°,
又∠1+∠4=180°,
∴∠4=180°﹣∠1=180°﹣45°=135°.
17.解:(1)∵OE平分∠COB,
∴∠COE=∠COB,
∵∠AOD=∠COB,
∴∠AOD=2∠COE;
(2)∵∠AOC=50°,
∴∠BOC=180°﹣50°=130°,
∴∠EOC=∠BOC=65°,
∴∠DOE=180°﹣∠EOC=180°﹣65°=115°,
∵OF平分∠DOE,
∴∠EOF=∠DOE=57.5°;
(3)设∠AOC=∠BOD=α,则∠DOF=α+15°,
∴∠EOF=∠DOF=α+15°,
∴∠EOB=∠EOF+∠BOF=α+30°,
∴∠COB=2∠EOB=2α+60°,
而∠COB+∠BOD=180°,即,3α+60°=180°,
解得,α=40°,
即,∠AOC=40°.
18.解:(1)直线l1,l2被直线l3所截,在这个基本图形中,形成了2对同旁内角.
(2)平面内三条直线l1,l2,l3两两相交,交点分别为A、B、C,图中一共有6对同旁内角.
(3)平面内四条直线两两相交,最多可以形成24对同旁内角.
(4)平面内n条直线两两相交,最多可以形成n(n﹣1)(n﹣2)对同旁内角
故答案为:(1)2;(2)6;(3)24;(4)n(n﹣1)(n﹣2)
一.选择题
1.下列各图中,∠1与∠2是对顶角的是( )
A. B.
C. D.
2.如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )
A.A点 B.B点 C.C点 D.D点
3.如图,下列结论中错误的是( )
A.∠1与∠2是同旁内角 B.∠1与∠4是内错角
C.∠5与∠6是内错角 D.∠3与∠5是同位角
4.如图,AB和CD相交于点O,则下列结论正确的是( )
A.∠1>∠2 B.∠2=∠3 C.∠1=∠4+∠5 D.∠2<∠5
5.如图,AC⊥BC,CD⊥AB,下列结论中,正确的结论有( )
①线段CD的长度是C点到AB的距离;
②线段AC的长度是A点到BC的距离;
③AB>AC>CD.
A.0个 B.1个 C.2个 D.3个
6.如图,给出以下说法:①∠B和∠1是同旁内角;②∠3和∠4是内错角;③∠B和∠AEC是同位角;④∠A和∠3是内错角;⑤∠2和∠3是对顶角,其中正确的个数是( )
A.4个 B.3个 C.2个 D.1个
7.如图所示,下列说法:
①∠1与∠C是同位角;
②∠2与∠C是内错角;
③∠3与∠B是同旁内角;
④∠3与∠C是同旁内角.
其中正确的是( )
A.①②③ B.②③④ C.①③④ D.①②④
8.如图,给出下列说法:①∠A和∠4是同位角;②∠1和∠3是对顶角;③∠2和∠4是内错角;④∠A和∠BCD是同旁内角.其中说法错误的有( )
A.1个 B.2个 C.3个 D.4个
9.如图,直线AB、CD与EF相交,则∠2的内错角是( )
A.∠8 B.∠7 C.∠6 D.∠4
10.观察如图,并阅读图形下面的相关文字:
两条直线相交,最多有1个交点;三条直线相交,最多有3个交点;4条直线相交,最多有6个交点……
像这样,20条直线相交,交点最多的个数是( )
A.100个 B.135个 C.190个 D.200个
二.填空题(共5小题)
11.已知线段AB与直线CD互相垂直,垂足为点O,且AO=5cm,BO=3cm,则线段AB的长为 .
12.如图,∠1和∠3是直线 和 被直线 所截而成的 角;图中与∠2是同旁内角的角有 个.
13.已知:直线AB与直线CD交于点O,∠BOC=45°,
(1)如图,若EO⊥AB,则∠DOE= .
(2)如图,若EO平分∠AOC,则∠DOE= .
14.如图,直线AB,CD相交于O,OE⊥AB,O为垂足,∠COE=34°,则∠BOD= 度.
15.如图①两条直线交于一点,图中共有=2对对顶角;如图②三条直线交于一点,图中共有=6对对顶角;如图③四条直线交于一点,图中共有=12对对顶角;…;按这样的规律,六条直线交于一点,那么图中共有 对对顶角.(只填数字)
三.解答题
16.如图,两条直线a,b相交.
(1)如果∠1=50°,求∠2,∠3的度数;
(2)如果∠2=3∠1,求∠3,∠4的度数.
17.如图,直线AB,CD交于点O,OE平分∠COB,OF是∠EOD的角平分线.
(1)说明:∠AOD=2∠COE;
(2)若∠AOC=50°,求∠EOF的度数;
(3)若∠BOF=15°,求∠AOC的度数.
18.复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想.
(1)如图1,直线l1,l2被直线l3所截,在这个基本图形中,形成了 对同旁内角.
(2)如图2,平面内三条直线l1,l2,l3两两相交,交点分别为A、B、C,图中一共有 对同旁内角.
(3)平面内四条直线两两相交,最多可以形成 对同旁内角.
(4)平面内n条直线两两相交,最多可以形成 对同旁内角.
参考答案
一.选择题
1.解:A、∠1与∠2不是对顶角;
B、∠1与∠2不是对顶角;
C、∠1与∠2不是对顶角;
D、∠1与∠2是对顶角;
故选:D.
2.解:根据垂线段最短可得:应建在A处,
故选:A.
3.解:如图,∠1与∠2是直线a与直线b被直线c所截的同旁内角,因此选项A不符合题意;
∠1与∠6是直线a与直线b被直线c所截的内错角,而∠6与∠4是邻补角,所以∠1与∠4不是内错角,因此选项B符合题意;
∠5与∠6是直线c与直线d被直线b所截的内错角,因此选项C不符合题意;
∠3与∠5是直线c与直线d被直线b所截的同位角,因此选项D不符合题意;
故选:B.
4.解:A.∵∠1与∠2是对顶角,
∴∠1=∠2,
故本选项不符合题意;
B.∵∠2是△AOD的外角,
∴∠2>∠3,
故本选项不符合题意;
C.∵∠1是△OBC的外角,
∴∠1=∠4+∠5,
故本选项符合题意;
D.∵∠2是△OBC的外角,
∴∠2>∠5,
故本选项不符合题意;
故选:C.
5.解:①线段CD的长度是C点到AB的距离,故结论正确;
②应该是线段AC的长度是A点到BC的距离,故结论正确;
③在同一直角三角形中,斜边大于直角边,所以AB>AC>CD,故结论正确;
故选:D.
6.解:∠B和∠1是直线AB和CE被直线BC所截的一对同旁内角,故①正确;
∠3和∠4不是内错角,故②错误;
∠B和∠AEC是直线CE和BC被直线AB所截的一对同位角,故③正确;
∠A和∠3是直线AB和CD被直线AC所截的一对内错角,故④正确;
∠2和∠3不是对顶角,故⑤错误;
即正确的有3个,
故选:B.
7.解:①∠1与∠C是同位角,说法正确;
②∠2与∠C是内错角,说法错误;
③∠3与∠B是同旁内角,说法正确;
④∠3与∠C是同旁内角,说法正确;
故选:C.
8.解:①∠A和∠4是同位角,说法正确;
②∠1和∠3是对顶角,说法错误;
③∠2和∠4是内错角,说法正确;
④∠A和∠BCD是同旁内角说法错误;
说法错误的有2个,
故选:B.
9.解:由题可得,∠2的内错角是∠7,
故选:B.
10.解:2条直线相交最多有1个交点,1=×1×2,
3条直线相交最多有3个交点,3=1+2=×2×3,
4条直线相交最多有6个交点,6=1+2+3=×3×4,
5条直线相交最多有10个交点,10=1+2+3+4=×4×5,
…
n条直线相交最多有交点的个数是:n(n﹣1).
20条直线相交最多有交点的个数是:n(n﹣1)=×20×19=190.
故选:C.
二.填空题(共5小题)
11.解:当点O在线段AB内时,AB=AO+BO=5cm+3cm=8cm,
当点O在线段AB外时,AB=AO﹣BO=5cm﹣3cm=2cm.
故答案为:8cm 或2cm.
12.解:∠1和∠3是直线AB和AC被直线DE所截而成的内错角;图中与∠2 是同旁内角的角有∠6、∠5、∠7,共3个,
故答案为:AB、AC、DE、内错,3.
13.解:(1)∵直线AB与直线CD相交,
∴∠AOD=∠BOC=45°.
∵EO⊥AB,
∴∠AOE=90°,
∴∠DOE=∠AOD+∠AOE=135°;
(2)∵直线AB与直线CD相交,
∴∠AOD=∠BOC=45°,∠AOC=135°,
∵EO平分∠AOC,
∴∠AOE=∠AOC=67.5°,
∴∠DOE=∠AOD+∠AOE=112.5°.
故答案为:135°;112.5°.
14.解:∵OE⊥AB,∠COE=34°,
∴∠BOD=90°﹣∠COE=90°﹣34°=56°.
故答案为:56.
15.解:由各图形直线的条数,以及计算对顶角个数的式子,可知
6条直线相交时,这个图形的对顶角的个数是:=30对对顶角.
三.解答题
16.解:(1)∵∠1=50°,∠1+∠2=180°,
∴∠2=180°﹣50°=130°,
又∵∠3与∠1是对顶角,
∴∠3=∠1=50°;
(2)∵∠2=3∠1,∠1+∠2=180°,
∴∠1+3∠1=180°,
∴4∠1=180°,
∴∠1=45°,
∴∠3=∠1=45°,
又∠1+∠4=180°,
∴∠4=180°﹣∠1=180°﹣45°=135°.
17.解:(1)∵OE平分∠COB,
∴∠COE=∠COB,
∵∠AOD=∠COB,
∴∠AOD=2∠COE;
(2)∵∠AOC=50°,
∴∠BOC=180°﹣50°=130°,
∴∠EOC=∠BOC=65°,
∴∠DOE=180°﹣∠EOC=180°﹣65°=115°,
∵OF平分∠DOE,
∴∠EOF=∠DOE=57.5°;
(3)设∠AOC=∠BOD=α,则∠DOF=α+15°,
∴∠EOF=∠DOF=α+15°,
∴∠EOB=∠EOF+∠BOF=α+30°,
∴∠COB=2∠EOB=2α+60°,
而∠COB+∠BOD=180°,即,3α+60°=180°,
解得,α=40°,
即,∠AOC=40°.
18.解:(1)直线l1,l2被直线l3所截,在这个基本图形中,形成了2对同旁内角.
(2)平面内三条直线l1,l2,l3两两相交,交点分别为A、B、C,图中一共有6对同旁内角.
(3)平面内四条直线两两相交,最多可以形成24对同旁内角.
(4)平面内n条直线两两相交,最多可以形成n(n﹣1)(n﹣2)对同旁内角
故答案为:(1)2;(2)6;(3)24;(4)n(n﹣1)(n﹣2)
