6.7一元一次不等式组

6.7一元一次不等式组
唐镇中学 王佳
一、教学目标
1、知识与技能：
（1）、知道什么是一元一次不等式组、不等式组的解集、解不等式组.
（2）、会解一元一次不等式组.
2、过程与方法：
（1）、经历通过具体问题抽象出不等式组的过程，让学生尝试归纳一元一次不等式组的概念 。
（2）、懂得一元一次不等式组解集的含义，初步渗透数形结合思想。
3、情感态度与价值观：
（1）、体验数学知识来源于生活，同时又服务与生活。
（2）、培养学生独立思考的习惯，同时还要培养合作交流的意识。
二、教学重点与难点
利用数轴确定一元一次不等式组的解集
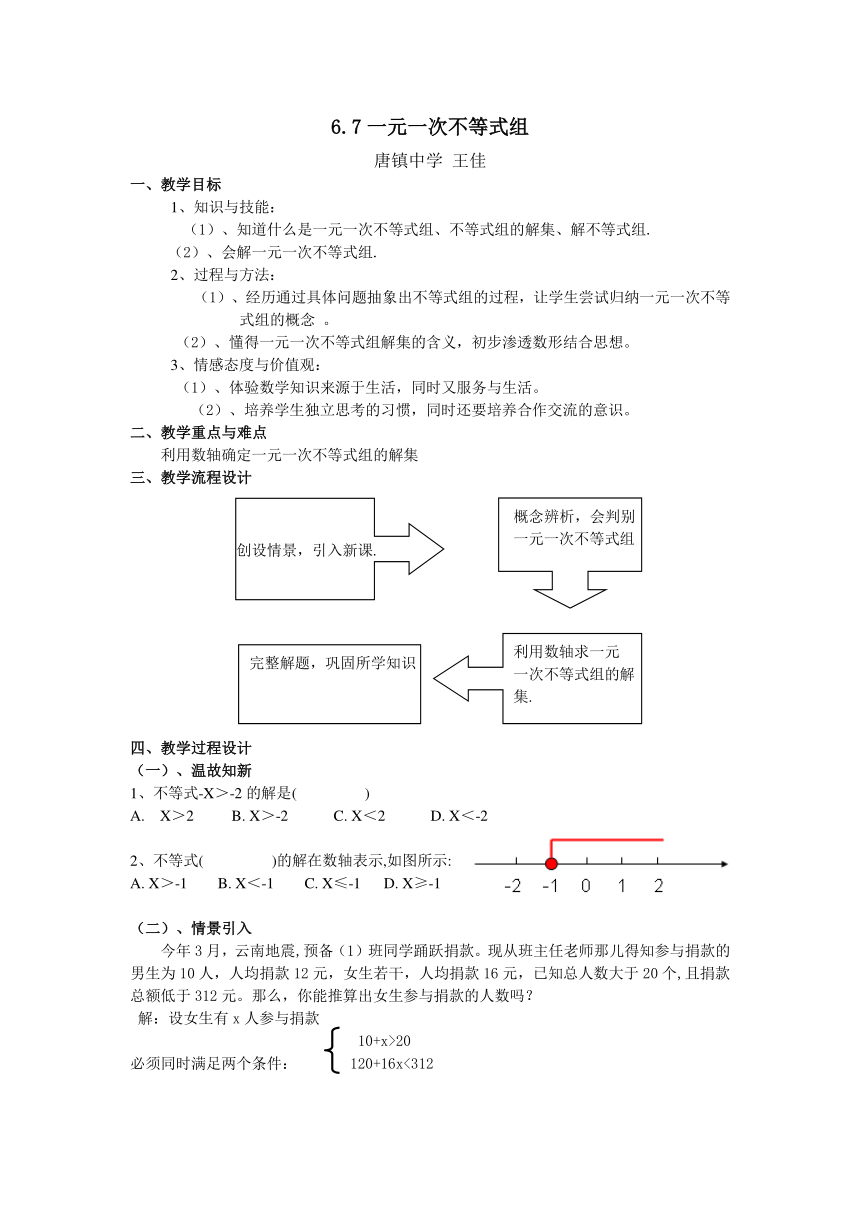
三、教学流程设计
四、教学过程设计
（一）、温故知新
1、不等式-X＞-2的解是( )
A. X＞2 B. X＞-2 C. X＜2 D. X＜-2
2、不等式( )的解在数轴表示,如图所示:
A. X＞-1 B. X＜-1 C. X≤-1 D. X≥-1
（二）、情景引入
今年3月，云南地震,预备（1）班同学踊跃捐款。现从班主任老师那儿得知参与捐款的男生为10人，人均捐款12元，女生若干，人均捐款16元，已知总人数大于20个,且捐款总额低于312元。那么，你能推算出女生参与捐款的人数吗？
解：设女生有x人参与捐款
10+x>20
必须同时满足两个条件： 120+16x<312
（三）、探索新知
定义: 一般地,由几个同一未知数的一元一次不等式所组成的一组不等式,叫做一元一次不等式组.
注意：
组成不等式组的不等式必须都是关于同一个未知数。
未知数的次数都是一次。
组成不等式组的不等式至少是2个。
1、判断一元一次不等式组（辨一辨）
判断下列不等式组是不是一元一次不等式组:
（1） y>3 （2） y2-y>3
y+1<2y y<-2y+1
(3) x>3 （4） a>3
y-4<-7 3a-1>0
a<-1
2、解一元一次不等式组（画一画）
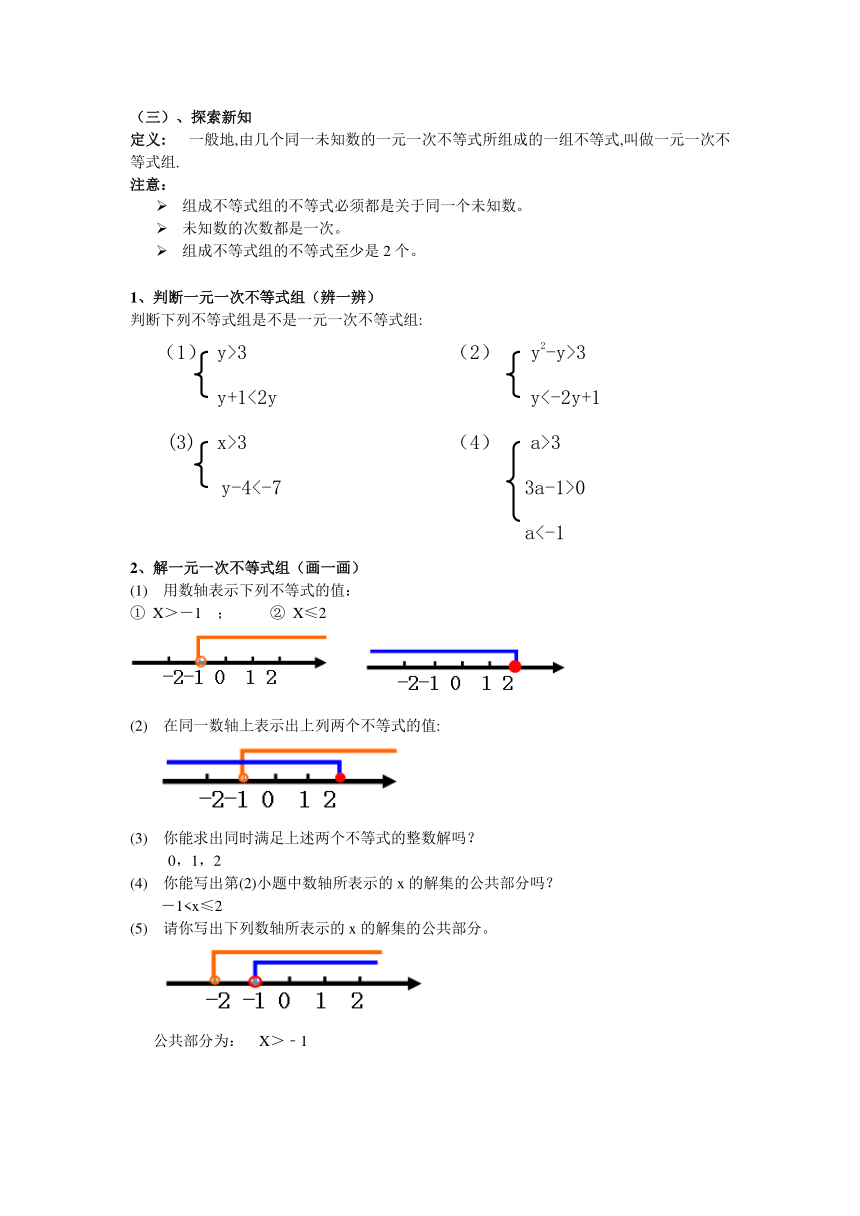
(1) 用数轴表示下列不等式的值：
① X＞－1 ；　 ② X≤2
(2) 在同一数轴上表示出上列两个不等式的值:
(3) 你能求出同时满足上述两个不等式的整数解吗？
0，1，2
(4) 你能写出第(2)小题中数轴所表示的x的解集的公共部分吗？
－1(5) 请你写出下列数轴所表示的x的解集的公共部分。
公共部分为： X＞﹣1
公共部分为： X≤﹣2
没有公共部分，故：无解
(6) 通过以上练习，你发现了什么？
定义: 组成不等式组的各个不等式的解集的公共部分就是不等式组的解集.
求不等式组的解集的过程叫做解不等式组。
注: 当它们没有公共部分时,则称这个不等式组无解.
3、找规律（记一记）
同大取大
同小取小
大小小大
中间找
大大小小
是无解
4、回到最初的问题：求女生捐款人数（注意解题格式）（算一算）
10+x>20 ①
12×10+16x<312 ②
解：由①，得 x > 10
由②，得 16x <312-120
16x<192
X<12
在数轴上表示不等式①，②的解集:
∴这个不等式组的解集是 10< x< 12
所以该班女生参与捐款的人数为11人.
解一元一次不等式组的一般步骤是：
求出各个不等式的解集；
把各个不等式的解集表示在同一数轴上；
找出它们的公共部分并写出解集。
5、练一练：（学生自做，上台演示）
5x－10＞2x－4
3（x－2）＋4≤25－（x＋6）
（四）、总结所学（归一归）
1、 一元一次不等式组的相关概念：
一元一次不等式组
不等式组的解集
2、 解一元一次不等式组的一般步骤:
求出各个不等式的解集；
把各个不等式的解集表示在同一数轴上；
找出它们的公共部分并写出解集。
（五）、拓展训练（试一试）
（六）、布置作业
练习册6.7
创设情景，引入新课.
完整解题，巩固所学知识
利用数轴求一元
一次不等式组的解
集.
概念辨析，会判别一元一次不等式组
0 2 4 6 8 10 12
3x－2＜2x＋3
4x≥8
5x－1＜29