北师大版八年级年级下册1.2.1直角三角形的性质与判定 课件(共29张PPT)
文档属性
| 名称 | 北师大版八年级年级下册1.2.1直角三角形的性质与判定 课件(共29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 08:14:01 | ||
图片预览





文档简介
1.2 直角三角形
第1课时 直角三角形的性质与判定
学习目标
一、了解直角三角形的性质。
二、掌握直角三角形的判定定理。
三、逆命题与逆定理的概念。
情境导入
我们曾经探索过直角三角形的哪些性质和判定方法?
想一想
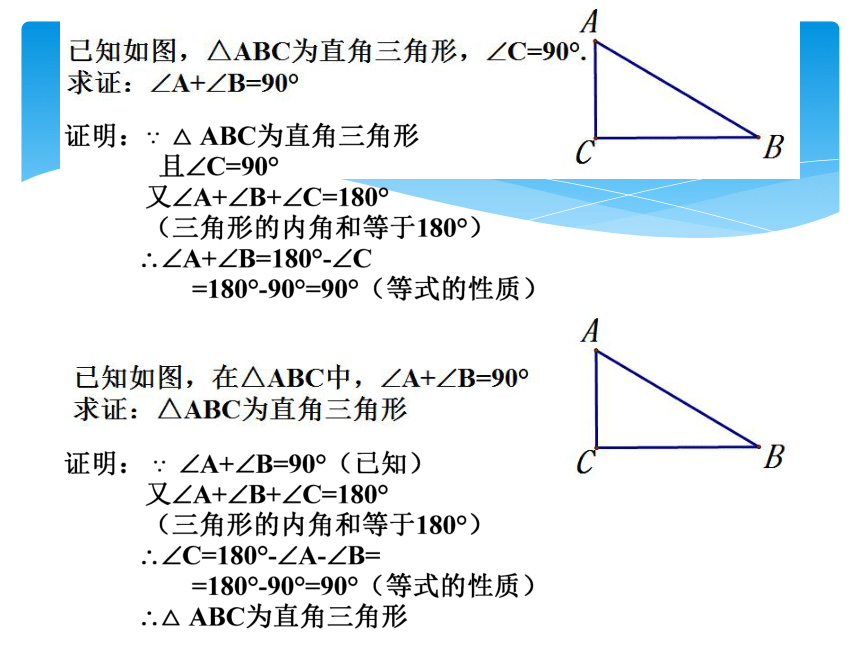
(1) 直角三角形的两个锐角有怎样的关系?为什么?
如果一个三角形有两个角互余,那么这个三角形
是直角三角形吗?为 什么?
体悟新知
直角三角形中角的关系:
归 纳
定理 直角三角形的两个锐角互余.
定理 有两个角互余的三角形是直角三角形.
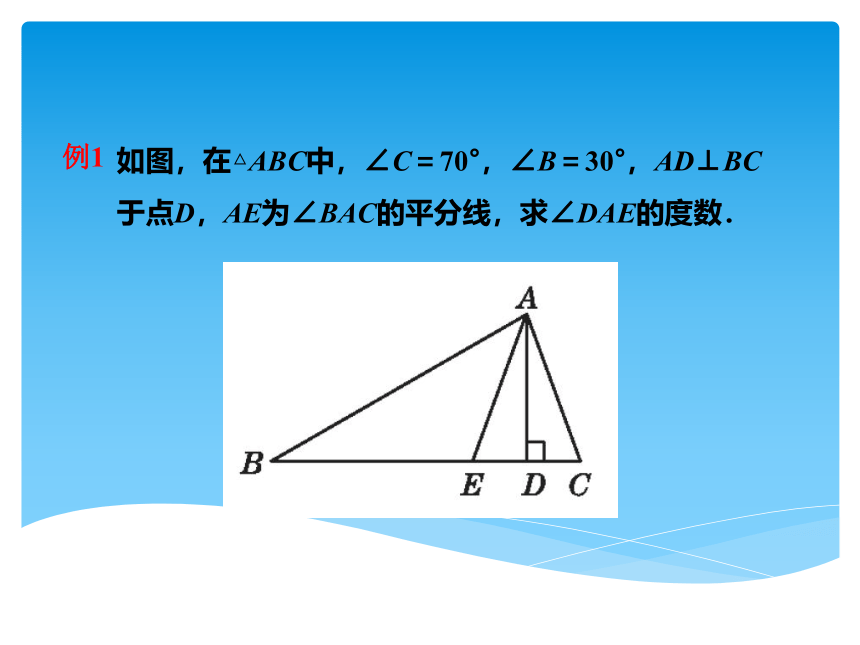
如图,在△ABC中,∠C=70°,∠B=30°,AD⊥BC于点D,AE为∠BAC的平分线,求∠DAE的度数.
例1
由题意可知,
∠BAC=180°-∠B-∠C
=180°-30°-70°=80°.
∵AE为∠BAC的平分线,
∴∠CAE=∠BAE= ∠BAC=40°.
∵AD⊥BC,∴∠ADC=90°.
∴∠CAD=90°-∠C=90°-70°=20°.
∴∠DAE=∠CAE-∠CAD=40°-20°=20°.
解:
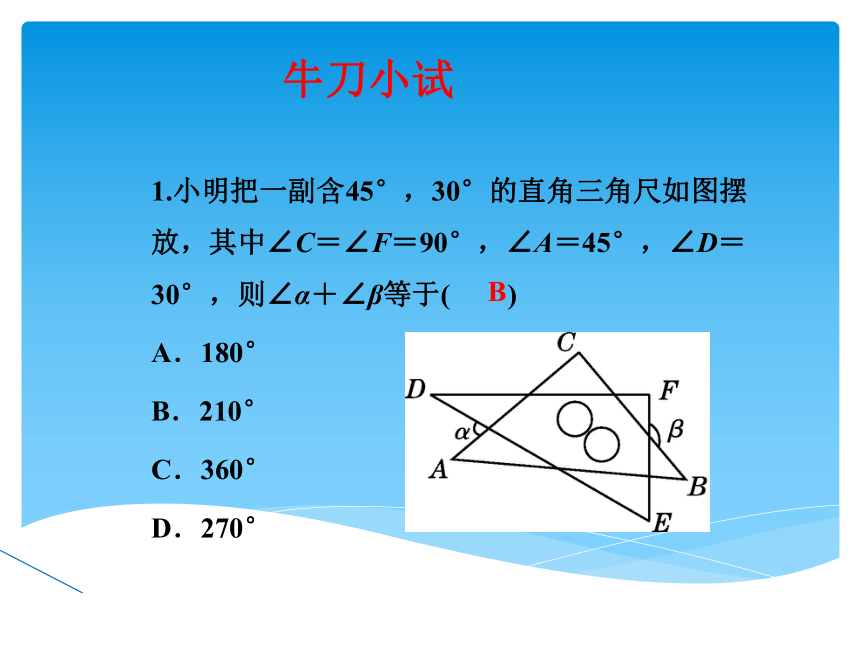
1.小明把一副含45°,30°的直角三角尺如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于( )
A.180°
B.210°
C.360°
D.270°
B
牛刀小试
知识
勾股定理 直角三角形两条直角边的平方和等于
斜边的平方.
A
C
B
直角三角形中边角关系
反过来,在一个三角形中,当两边的平方和等于第三边的平方时,我们曾用度量的办法得出“这个三角形是直角三角形”的结论.下面我们证明这个结论.
已知:如图 (1),在△ABC中,AB2+AC2=BC2.
求证:△ABC是直角三角形
证明:
如图(2) ,作Rt △A′B′C′ ,使
∠A′=90° A′B′=AB, A′C′=AC,
则A′B′ 2+A′C′ 2 =B′C′ 2(勾股定理).
∵AB2+AC2=BC2 ,
∴BC2 = B′C′ 2.
∴BC = B′C′.
∴△ABC≌ △A′B′C′ (SSS).
∴ ∠A=∠A′=90°(全等三角形的对应角相等).
因此, △ABC是直角三角形.
定理总结
勾股定理:直角三角形两条直角边的平方和等于斜边的平方。
定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
例2
A
如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
过点C作CD⊥AB于点D,
则S△ABC= AC·BC= AB·CD,
∴AC·BC=AB·CD.又由方法一知AB=15,
∴CD= ,即点C到AB的距离为 .
1.如图,将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起,其中点A′与点A重合,点C′落在边AB上,连接B′C. 若∠ACB=∠AC′B′=90°,AC=BC=3,则B′C的长为( )
A.3
B.6
C.3
D.
A
初试锋芒
2.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为
13,则小正方形的面积为( )
A.3 B.4
C.5 D.6
C
3.如图是一棵美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的边长分别是3,5,2,3,则正方形E的面积是( )
A.13
B.26
C.47
D.94
C
4.我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图,把枯木看作一个圆柱体,因一丈是10尺,则该圆柱的高为20尺,底面周长为3尺,
有葛藤自点A处缠绕而上,绕5周
后其末端恰好到达点B处.则问
题中葛藤的最短长度是________.
25尺
观察上面第一个定理和第二个定理,它们的条件和结论之间有怎样的关系?第三个定理和第四个定理呢?与同伴交流.
再观察下面三组命题:
(1)如果两个角是对顶角,那么它们相等;
如果两个角相等,那么它们是对顶角.
(2)如果小明患了肺炎,那么他一定会发烧;
如果小明发烧,那么他一定患了肺炎.
逆命题和逆定理
(3)一个三角形中相等的边所对的角相等;
一个三角形中相等的角所对的边相等.
上面每组中两个命题的条件和结论也有类似的关系吗?与同伴交流.
1.在两个命题中,如果一个命题的条件和结论分别
是另一个命题的结论和条件,那么这两个命题称
为互逆命题,其中一个命题称为另一个命题的逆
命题.
2.如果一个定理的逆命题经过证明是真命题,那么
它也是一个定理,其中一个定理称为另一个定理
的逆定理,这两个定理称为互逆定理.
例3
判断下列命题的真假,写出逆命题,并判断逆命题的真假:
(1)如果两条直线相交,那么它们只有一个交点;
(2)如果a>b,那么a2>b2;
(3)如果两个数互为相反数,那么它们的和为零;
(4)如果ab<0,那么a>0,b<0.
导引:
根据题目要求,先判断原命题的真假,再将原命题
的题设和结论部分互换,写出原命题的逆命题,最
后判断逆命题的真假.
解:
(1)原命题是真命题.逆命题为:如果两条直线只有
一个交点,那么它们相交.逆命题是真命题.
(2)原命题是假命题.逆命题为:如果a2>b2,那么a
>b.逆命题是假命题.
(3)原命题是真命题.逆命题为:如果两个数的和为
零,那么它们互为相反数.逆命题是真命题.
(4)原命题是假命题.逆命题为:如果a>0,b<0,
那么ab<0.逆命题是真命题.
总 结
写出逆命题的关键是分清楚原命题的题设和结
论,然后将它的题设和结论交换位置就得到这个命
题的逆命题.判断一个命题是真命题需要进行逻辑
推理,判断一个命题是假命题只需要举出反例就可
以了.
1.说出下列命题的逆命题,并判断每对命题的真假:
(1)四边形是多边形;
(2)两直线平行,同旁内角互补;
(3)如果ab=0,那么a=0,b=0.
(来自《教材》)
(1)逆命题:多边形是四边形.原命题真,逆命题假.
(2)逆命题:同旁内角互补,两直线平行.原命题真,
逆命题真.
(3)逆命题:如果 a=0,b=0,那么ab=0. 原命题假,
逆命题真.
解:
2.下列说法正确的是( )
A.每个定理都有逆定理
B.每个命题都有逆命题
C.原命题是假命题,则它的逆命题也是假命题
D.真命题的逆命题是真命题
B
3.一直角三角形的两边长分别为3和4,则第三边的长为( )
A.5 B.
C. D.5或
易错点:考虑问题不全面而漏解
D
直角三角形角的关系:
定理 直角三角形的两个锐角互余.
定理 有两个角互余的三角形是直角三角形.
今天我们学了什么?
(2)勾股定理及其逆定理:
勾股定理 直角三角形两条直角边的平方和等于斜边的平方.
勾股定理逆定理 如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
(3)互逆命题、互逆定理:
第1课时 直角三角形的性质与判定
学习目标
一、了解直角三角形的性质。
二、掌握直角三角形的判定定理。
三、逆命题与逆定理的概念。
情境导入
我们曾经探索过直角三角形的哪些性质和判定方法?
想一想
(1) 直角三角形的两个锐角有怎样的关系?为什么?
如果一个三角形有两个角互余,那么这个三角形
是直角三角形吗?为 什么?
体悟新知
直角三角形中角的关系:
归 纳
定理 直角三角形的两个锐角互余.
定理 有两个角互余的三角形是直角三角形.
如图,在△ABC中,∠C=70°,∠B=30°,AD⊥BC于点D,AE为∠BAC的平分线,求∠DAE的度数.
例1
由题意可知,
∠BAC=180°-∠B-∠C
=180°-30°-70°=80°.
∵AE为∠BAC的平分线,
∴∠CAE=∠BAE= ∠BAC=40°.
∵AD⊥BC,∴∠ADC=90°.
∴∠CAD=90°-∠C=90°-70°=20°.
∴∠DAE=∠CAE-∠CAD=40°-20°=20°.
解:
1.小明把一副含45°,30°的直角三角尺如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于( )
A.180°
B.210°
C.360°
D.270°
B
牛刀小试
知识
勾股定理 直角三角形两条直角边的平方和等于
斜边的平方.
A
C
B
直角三角形中边角关系
反过来,在一个三角形中,当两边的平方和等于第三边的平方时,我们曾用度量的办法得出“这个三角形是直角三角形”的结论.下面我们证明这个结论.
已知:如图 (1),在△ABC中,AB2+AC2=BC2.
求证:△ABC是直角三角形
证明:
如图(2) ,作Rt △A′B′C′ ,使
∠A′=90° A′B′=AB, A′C′=AC,
则A′B′ 2+A′C′ 2 =B′C′ 2(勾股定理).
∵AB2+AC2=BC2 ,
∴BC2 = B′C′ 2.
∴BC = B′C′.
∴△ABC≌ △A′B′C′ (SSS).
∴ ∠A=∠A′=90°(全等三角形的对应角相等).
因此, △ABC是直角三角形.
定理总结
勾股定理:直角三角形两条直角边的平方和等于斜边的平方。
定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
例2
A
如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
过点C作CD⊥AB于点D,
则S△ABC= AC·BC= AB·CD,
∴AC·BC=AB·CD.又由方法一知AB=15,
∴CD= ,即点C到AB的距离为 .
1.如图,将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起,其中点A′与点A重合,点C′落在边AB上,连接B′C. 若∠ACB=∠AC′B′=90°,AC=BC=3,则B′C的长为( )
A.3
B.6
C.3
D.
A
初试锋芒
2.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为
13,则小正方形的面积为( )
A.3 B.4
C.5 D.6
C
3.如图是一棵美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的边长分别是3,5,2,3,则正方形E的面积是( )
A.13
B.26
C.47
D.94
C
4.我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图,把枯木看作一个圆柱体,因一丈是10尺,则该圆柱的高为20尺,底面周长为3尺,
有葛藤自点A处缠绕而上,绕5周
后其末端恰好到达点B处.则问
题中葛藤的最短长度是________.
25尺
观察上面第一个定理和第二个定理,它们的条件和结论之间有怎样的关系?第三个定理和第四个定理呢?与同伴交流.
再观察下面三组命题:
(1)如果两个角是对顶角,那么它们相等;
如果两个角相等,那么它们是对顶角.
(2)如果小明患了肺炎,那么他一定会发烧;
如果小明发烧,那么他一定患了肺炎.
逆命题和逆定理
(3)一个三角形中相等的边所对的角相等;
一个三角形中相等的角所对的边相等.
上面每组中两个命题的条件和结论也有类似的关系吗?与同伴交流.
1.在两个命题中,如果一个命题的条件和结论分别
是另一个命题的结论和条件,那么这两个命题称
为互逆命题,其中一个命题称为另一个命题的逆
命题.
2.如果一个定理的逆命题经过证明是真命题,那么
它也是一个定理,其中一个定理称为另一个定理
的逆定理,这两个定理称为互逆定理.
例3
判断下列命题的真假,写出逆命题,并判断逆命题的真假:
(1)如果两条直线相交,那么它们只有一个交点;
(2)如果a>b,那么a2>b2;
(3)如果两个数互为相反数,那么它们的和为零;
(4)如果ab<0,那么a>0,b<0.
导引:
根据题目要求,先判断原命题的真假,再将原命题
的题设和结论部分互换,写出原命题的逆命题,最
后判断逆命题的真假.
解:
(1)原命题是真命题.逆命题为:如果两条直线只有
一个交点,那么它们相交.逆命题是真命题.
(2)原命题是假命题.逆命题为:如果a2>b2,那么a
>b.逆命题是假命题.
(3)原命题是真命题.逆命题为:如果两个数的和为
零,那么它们互为相反数.逆命题是真命题.
(4)原命题是假命题.逆命题为:如果a>0,b<0,
那么ab<0.逆命题是真命题.
总 结
写出逆命题的关键是分清楚原命题的题设和结
论,然后将它的题设和结论交换位置就得到这个命
题的逆命题.判断一个命题是真命题需要进行逻辑
推理,判断一个命题是假命题只需要举出反例就可
以了.
1.说出下列命题的逆命题,并判断每对命题的真假:
(1)四边形是多边形;
(2)两直线平行,同旁内角互补;
(3)如果ab=0,那么a=0,b=0.
(来自《教材》)
(1)逆命题:多边形是四边形.原命题真,逆命题假.
(2)逆命题:同旁内角互补,两直线平行.原命题真,
逆命题真.
(3)逆命题:如果 a=0,b=0,那么ab=0. 原命题假,
逆命题真.
解:
2.下列说法正确的是( )
A.每个定理都有逆定理
B.每个命题都有逆命题
C.原命题是假命题,则它的逆命题也是假命题
D.真命题的逆命题是真命题
B
3.一直角三角形的两边长分别为3和4,则第三边的长为( )
A.5 B.
C. D.5或
易错点:考虑问题不全面而漏解
D
直角三角形角的关系:
定理 直角三角形的两个锐角互余.
定理 有两个角互余的三角形是直角三角形.
今天我们学了什么?
(2)勾股定理及其逆定理:
勾股定理 直角三角形两条直角边的平方和等于斜边的平方.
勾股定理逆定理 如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
(3)互逆命题、互逆定理:
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
