第20章 一次函数 单元测试卷 (解析版)
文档属性
| 名称 | 第20章 一次函数 单元测试卷 (解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 231.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 08:39:37 | ||
图片预览



文档简介
第20章 一次函数 单元测试卷
一.选择题(共6小题)
1.下列关于x的函数中,一次函数是( )
A.y=kx+1 B.y=x+ C.y=﹣ D.y=﹣5x
2.函数y=5﹣2x,y的值随x值的增大而( )
A.增大 B.减小
C.不变 D.先增大后减小
3.一次函数y=﹣3x﹣1的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.直线y=﹣2x+6与两坐标轴围成的三角形的面积是( )
A.8 B.6 C.9 D.2
5.如图,直线y=﹣x+6与x轴,y轴分别交于点A和点B,点M是线段AB的中点,则线段OM的长为( )
A.4.8 B.5 C.6 D.8
6.若一次函数y=(1+2k)x+k﹣1的图象不经过第一象限,则k的取值范围是( )
A.k<﹣ B.﹣≤k<1且k≠0
C.﹣<k≤1 D.k≥1
二.填空题(共12小题)
7.已知一次函数y=(m﹣1)x|m|﹣2,则m= .
8.已知一次函数y=kx+1的图象经过点P(﹣1,0),则k= .
9.直线y=kx+b与直线y=3x﹣1平行,则k的值是 .
10.已知点(2,1)在直线y=kx﹣1上,则y随x的增大而 (填“增大”或“减小”).
11.直线y=2x﹣4向右平移m个单位后的解析式为y=2x﹣10,则m= .
12.若一次函数y=(1﹣m)x+2,函数值y随x的增大而减小,则m的取值范围是 .
13.若一次函数y=(2m﹣1)x+3的图象,y随x的增大而减小,则m的取值范围是 .
14.已知点A(a,﹣2),B(b,﹣4)在直线y=﹣x+6上,则a、b的大小关系是a b.
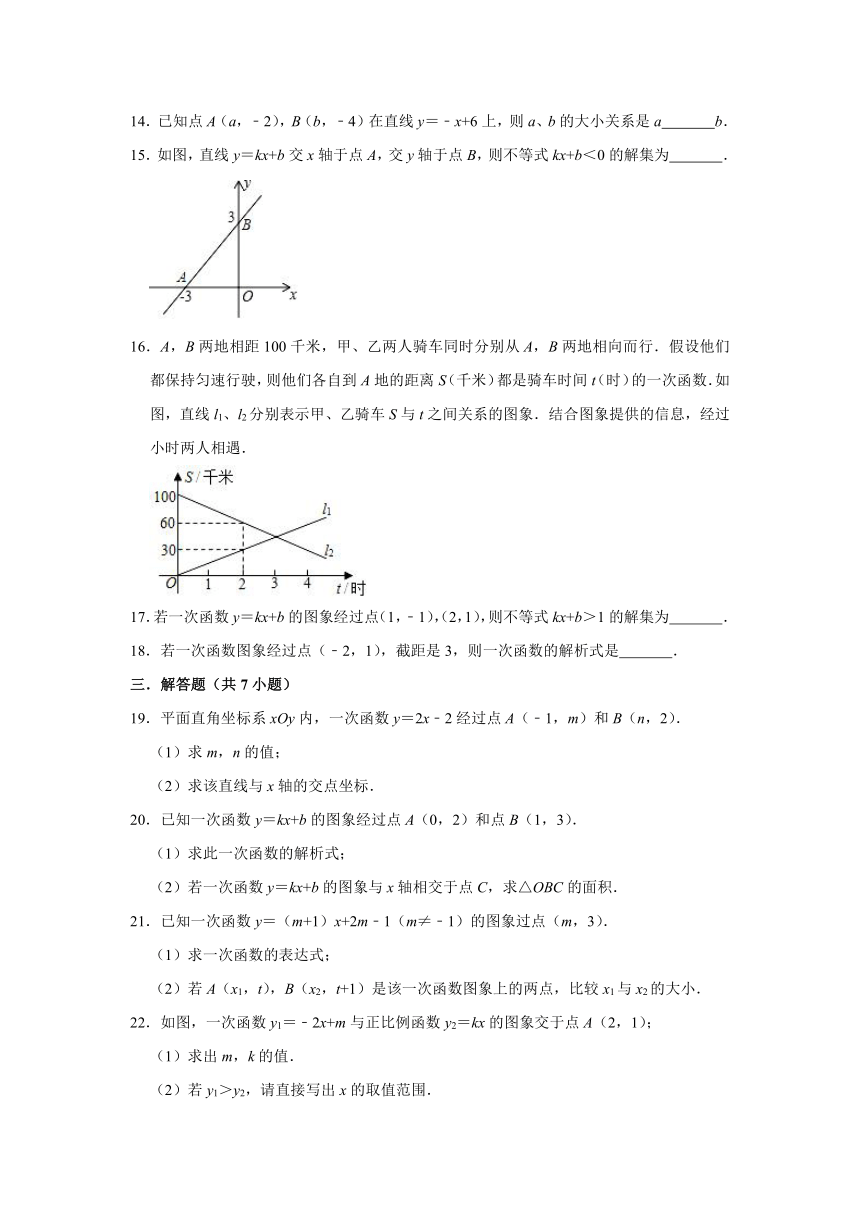
15.如图,直线y=kx+b交x轴于点A,交y轴于点B,则不等式kx+b<0的解集为 .
16.A,B两地相距100千米,甲、乙两人骑车同时分别从A,B两地相向而行.假设他们都保持匀速行驶,则他们各自到A地的距离S(千米)都是骑车时间t(时)的一次函数.如图,直线l1、l2分别表示甲、乙骑车S与t之间关系的图象.结合图象提供的信息,经过 小时两人相遇.
17.若一次函数y=kx+b的图象经过点(1,﹣1),(2,1),则不等式kx+b>1的解集为 .
18.若一次函数图象经过点(﹣2,1),截距是3,则一次函数的解析式是 .
三.解答题(共7小题)
19.平面直角坐标系xOy内,一次函数y=2x﹣2经过点A(﹣1,m)和B(n,2).
(1)求m,n的值;
(2)求该直线与x轴的交点坐标.
20.已知一次函数y=kx+b的图象经过点A(0,2)和点B(1,3).
(1)求此一次函数的解析式;
(2)若一次函数y=kx+b的图象与x轴相交于点C,求△OBC的面积.
21.已知一次函数y=(m+1)x+2m﹣1(m≠﹣1)的图象过点(m,3).
(1)求一次函数的表达式;
(2)若A(x1,t),B(x2,t+1)是该一次函数图象上的两点,比较x1与x2的大小.
22.如图,一次函数y1=﹣2x+m与正比例函数y2=kx的图象交于点A(2,1);
(1)求出m,k的值.
(2)若y1>y2,请直接写出x的取值范围.
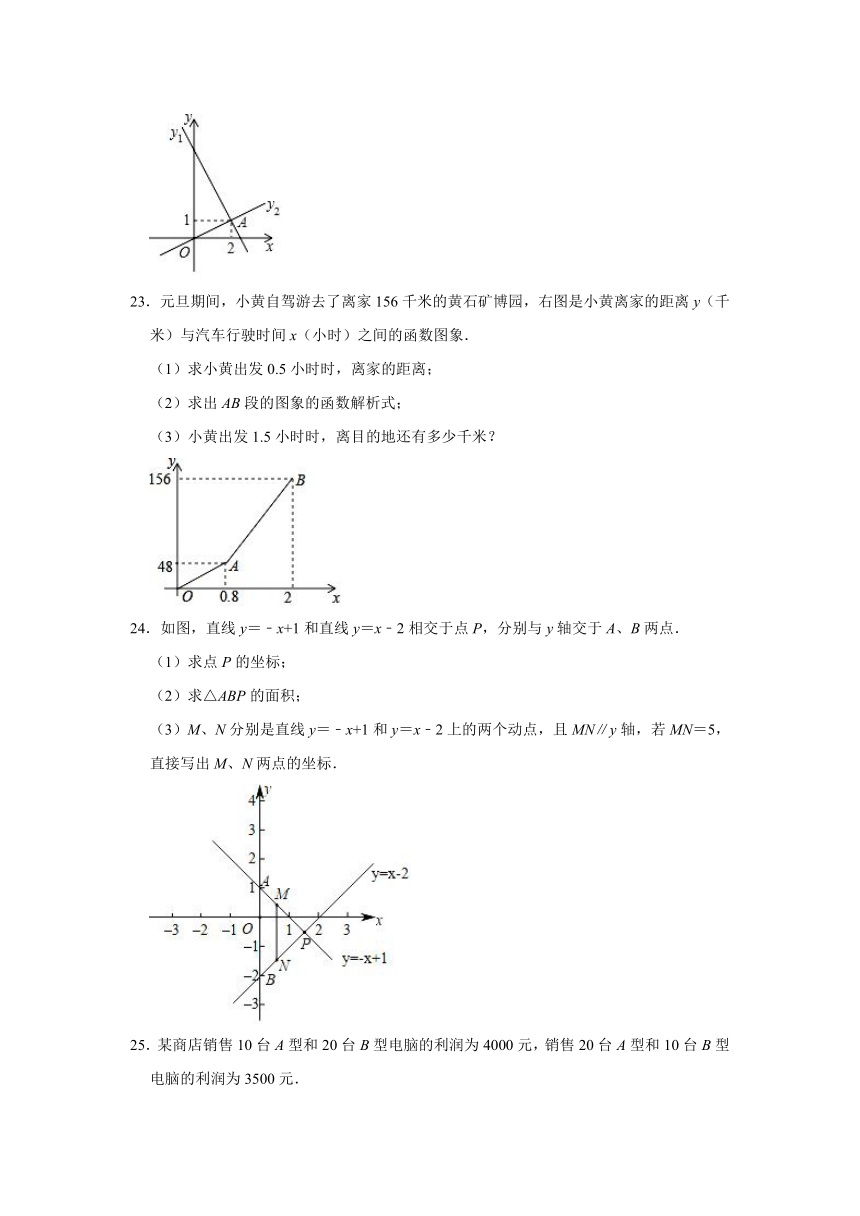
23.元旦期间,小黄自驾游去了离家156千米的黄石矿博园,右图是小黄离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
(1)求小黄出发0.5小时时,离家的距离;
(2)求出AB段的图象的函数解析式;
(3)小黄出发1.5小时时,离目的地还有多少千米?
24.如图,直线y=﹣x+1和直线y=x﹣2相交于点P,分别与y轴交于A、B两点.
(1)求点P的坐标;
(2)求△ABP的面积;
(3)M、N分别是直线y=﹣x+1和y=x﹣2上的两个动点,且MN∥y轴,若MN=5,直接写出M、N两点的坐标.
25.某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?最大利润是多少?
参考答案
一.选择题(共6小题)
1.下列关于x的函数中,一次函数是( )
A.y=kx+1 B.y=x+ C.y=﹣ D.y=﹣5x
解:A、y=kx+1,没有k≠0的条件,不是一次函数,不符合题意;
B、x在分母中,不是一次函数,不符合题意;
C、是反比例函数,不是一次函数,不符合题意;
D、符合一次函数的定义,是一次函数,符合题意;
故选:D.
2.函数y=5﹣2x,y的值随x值的增大而( )
A.增大 B.减小
C.不变 D.先增大后减小
解:∵y=5﹣2x,k=﹣2<0,
∴y的值随x值的增大而减小,
故选:B.
3.一次函数y=﹣3x﹣1的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
解:∵一次函数y=﹣3x﹣1,k=﹣3,b=﹣1,
∴该函数图象经过第二、三、四象限,不经过第一象限,
故选:A.
4.直线y=﹣2x+6与两坐标轴围成的三角形的面积是( )
A.8 B.6 C.9 D.2
解:在直线y=﹣2x+6中,
当x=0时,y=6;
当y=0时,x=3;
∴直线y=﹣2x+6与坐标轴交于(0,6),(3,0)两点,
∴直线y=﹣2x+6与两坐标轴围成的三角形面积=×6×3=9.
故选:C.
5.如图,直线y=﹣x+6与x轴,y轴分别交于点A和点B,点M是线段AB的中点,则线段OM的长为( )
A.4.8 B.5 C.6 D.8
解:把x=0代入y=﹣x+6得:
y=6,
即点B的坐标为(0,6),
把y=0代入y=﹣x+6得:
﹣x+6=0,
解得:x=8,
即点A的坐标为(8,0),
∴AB==10,
∵点M是线段AB的中点,
∴OM=AB=5,
故选:B.
6.若一次函数y=(1+2k)x+k﹣1的图象不经过第一象限,则k的取值范围是( )
A.k<﹣ B.﹣≤k<1且k≠0
C.﹣<k≤1 D.k≥1
解:当一次函数y=(1+2k)x+k﹣1的图象经过第二、四象限时,,无解,舍去;
当一次函数y=(1+2k)x+k﹣1的图象经过第二、三、四象限时,,
解得:k<﹣.
故选:A.
二.填空题(共12小题)
7.已知一次函数y=(m﹣1)x|m|﹣2,则m= ﹣1 .
解:∵y=(m﹣1)x|m|﹣2是一次函数,
∴|m|=1,m﹣1≠0,
解得m=﹣1.
故答案为:﹣1.
8.已知一次函数y=kx+1的图象经过点P(﹣1,0),则k= 1 .
解:∵一次函数y=kx+1的图象经过点P(﹣1,0),
∴0=﹣k+1
∴k=1
故答案为:1
9.直线y=kx+b与直线y=3x﹣1平行,则k的值是 3 .
解:∵直线y=kx+b与直线y=3x﹣1平行,
∴k=3,
故答案为3.
10.已知点(2,1)在直线y=kx﹣1上,则y随x的增大而 增大 (填“增大”或“减小”).
解:∵点(2,1)在直线y=kx﹣1上,
∴1=2k﹣1,
∴k=1.
又∵k=1>0,
∴y随x的增大而增大.
故答案为:增大.
11.直线y=2x﹣4向右平移m个单位后的解析式为y=2x﹣10,则m= 3 .
解:∵直线y=2x﹣4向右平移m个单位后的解析式为y=2x﹣10,
∴y=2(x﹣m)﹣4=2x﹣10,
则﹣2m﹣4=﹣10,
解得:m=3.
故答案为:3.
12.若一次函数y=(1﹣m)x+2,函数值y随x的增大而减小,则m的取值范围是 m>1 .
解:∵一次函数y=(1﹣m)x+2,y随x的增大而减小,
∴1﹣m<0,
解得,m>1.
故答案是:m>1.
13.若一次函数y=(2m﹣1)x+3的图象,y随x的增大而减小,则m的取值范围是 .
解:∵函数值y随自变量x的增大而减小,
∴2m﹣1<0,
∴m<.
故答案为m.
14.已知点A(a,﹣2),B(b,﹣4)在直线y=﹣x+6上,则a、b的大小关系是a < b.
解:因为﹣1<0,一次函数y随x的增大而减小,
又﹣2>﹣4,
所以,a<b.
15.如图,直线y=kx+b交x轴于点A,交y轴于点B,则不等式kx+b<0的解集为 x<﹣3 .
解:∵直线y=kx+b交x轴于A(﹣3,0),
∴点A左边的部分的x的值满足不等式kx+b<0,
∴不等式kx+b<0的解集是x<﹣3.
故答案为:x<﹣3.
16.A,B两地相距100千米,甲、乙两人骑车同时分别从A,B两地相向而行.假设他们都保持匀速行驶,则他们各自到A地的距离S(千米)都是骑车时间t(时)的一次函数.如图,直线l1、l2分别表示甲、乙骑车S与t之间关系的图象.结合图象提供的信息,经过 小时两人相遇.
解:设l1的关系式为:s1=kt,则30=k×2,解得:k=15,故s1=15t;
设s2=at+b,将(0,100),(2,60),
则,
解得:,
故l2的关系式为s2=﹣20t+100;
15t=﹣20t+100,
t=.
即他们经过小时两人相遇.
故答案为:
17.若一次函数y=kx+b的图象经过点(1,﹣1),(2,1),则不等式kx+b>1的解集为 x>2 .
解:如图所示:不等式kx+b>1的解为:x>2.
故答案为x>2.
18.若一次函数图象经过点(﹣2,1),截距是3,则一次函数的解析式是 y=x+3 .
解:截距为3,说明b=3,那么可设所求的函数解析式为y=kx+3,经过点(﹣2,1),
代入函数解析式得:﹣2k+3=1,解得k=1.
∴一次函数的解析式是y=x+3.
三.解答题(共7小题)
19.平面直角坐标系xOy内,一次函数y=2x﹣2经过点A(﹣1,m)和B(n,2).
(1)求m,n的值;
(2)求该直线与x轴的交点坐标.
解:(1)当x=﹣1时,y=2×(﹣1)﹣2=﹣4,
∴m=﹣4;
当y=2时,2x﹣2=2,解得:x=2,
∴n=2.
(2)当y=0时,2x﹣2=0,解得:x=1,
∴该直线与x轴的交点坐标为(1,0).
20.已知一次函数y=kx+b的图象经过点A(0,2)和点B(1,3).
(1)求此一次函数的解析式;
(2)若一次函数y=kx+b的图象与x轴相交于点C,求△OBC的面积.
解:(1)∵一次函数y=kx+b的图象经过点A(0,2)和点B(1,3),
∴,
解得:,
∴一次函数解析式为y=x+2;
(2)∵当y=0时,x+2=0,
解得x=﹣2,
∴与x轴相交于点C坐标为(﹣2,0),
∴S△OBC=2×3=3.
21.已知一次函数y=(m+1)x+2m﹣1(m≠﹣1)的图象过点(m,3).
(1)求一次函数的表达式;
(2)若A(x1,t),B(x2,t+1)是该一次函数图象上的两点,比较x1与x2的大小.
解:(1)∵一次函数y=(m+1)x+2m﹣1(m≠﹣1)的图象过点(m,3).
∴3=(m+1)m+2m﹣1,
解得m1=1,m2=﹣4,
∴一次函数的表达式为y=2x+1或y=﹣3x﹣9;
(2)若A(x1,t),B(x2,t+1)是一次函数y=2x+1图象上的两点,
∵k=2>0,
∴y随x的增大而增大,
∵t<t+1,
∴x1<x2;
若A(x1,t),B(x2,t+1)是一次函数y=﹣3x﹣9图象上的两点,
∵k=﹣3<0,
∴y随x的增大而减小,
∵t<t+1,
∴x1>x2.
22.如图,一次函数y1=﹣2x+m与正比例函数y2=kx的图象交于点A(2,1);
(1)求出m,k的值.
(2)若y1>y2,请直接写出x的取值范围.
解:(1)∵一次函数y1=﹣2x+m与正比例函数y2=kx的图象交于点A(2,1),
∴把A的坐标代入函数解析式得:1=﹣4+m,1=2k,
解得:m=5,k=;
(2)由图象可知,若y1>y2,则x的取值范围是x<2.
23.元旦期间,小黄自驾游去了离家156千米的黄石矿博园,右图是小黄离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
(1)求小黄出发0.5小时时,离家的距离;
(2)求出AB段的图象的函数解析式;
(3)小黄出发1.5小时时,离目的地还有多少千米?
解:(1)设OA段图象的函数表达式为y=kx.
∵当x=0.8时,y=48,
∴0.8k=48,
∴k=60.
∴y=60x(0≤x≤0.8),
∴当x=0.5时,y=60×0.5=30.
故小黄出发0.5小时时,离家30千米;
(2)设AB段图象的函数表达式为y=k′x+b.
∵A(0.8,48),B(2,156)在AB上,
,
解得,
∴y=90x﹣24(0.8≤x≤2);
(3)∵当x=1.5时,y=90×1.5﹣24=111,
∴156﹣111=45.
故小黄出发1.5小时时,离目的地还有45千米.
24.如图,直线y=﹣x+1和直线y=x﹣2相交于点P,分别与y轴交于A、B两点.
(1)求点P的坐标;
(2)求△ABP的面积;
(3)M、N分别是直线y=﹣x+1和y=x﹣2上的两个动点,且MN∥y轴,若MN=5,直接写出M、N两点的坐标.
解:(1)∵直线y=﹣x+1和直线y=x﹣2相交于点P
∴,
解之得:,
∴P点坐标为:,
(2)∵直线y=﹣x+1和直线y=x﹣2分别交y轴于A、B两点
∴A(0,1),B(0,﹣2),
∴AB=3,
由(1)知P
∴S△ABP==;
(3)设M(m,﹣m+1),则N(m,m﹣2),
∵MN=5,
∴|﹣m+1﹣(m﹣2)|=5,
解得m=﹣1或m=4,
∴M(4,﹣3),N(4,2)或M(﹣1,2),N(﹣1,﹣3).
25.某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?最大利润是多少?
解:(1)设每台A型电脑销售利润为a元,每台B型电脑的销售利润为b元;
根据题意得,
解得.
答:每台A型电脑销售利润为100元,每台B型电脑的销售利润为150元;
(2)①根据题意得,y=100x+150(100﹣x),
即y=﹣50x+15000;
②据题意得,100﹣x≤2x,
解得x≥33,
∵y=﹣50x+15000,
∴y随x的增大而减小,
∵x为正整数,
∴当x=34时,y取最大值,则100﹣x=66,
此时最大利润是y=﹣50×34+15000=13300.
即商店购进34台A型电脑和66台B型电脑的销售利润最大,最大利润是13300元.
一.选择题(共6小题)
1.下列关于x的函数中,一次函数是( )
A.y=kx+1 B.y=x+ C.y=﹣ D.y=﹣5x
2.函数y=5﹣2x,y的值随x值的增大而( )
A.增大 B.减小
C.不变 D.先增大后减小
3.一次函数y=﹣3x﹣1的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.直线y=﹣2x+6与两坐标轴围成的三角形的面积是( )
A.8 B.6 C.9 D.2
5.如图,直线y=﹣x+6与x轴,y轴分别交于点A和点B,点M是线段AB的中点,则线段OM的长为( )
A.4.8 B.5 C.6 D.8
6.若一次函数y=(1+2k)x+k﹣1的图象不经过第一象限,则k的取值范围是( )
A.k<﹣ B.﹣≤k<1且k≠0
C.﹣<k≤1 D.k≥1
二.填空题(共12小题)
7.已知一次函数y=(m﹣1)x|m|﹣2,则m= .
8.已知一次函数y=kx+1的图象经过点P(﹣1,0),则k= .
9.直线y=kx+b与直线y=3x﹣1平行,则k的值是 .
10.已知点(2,1)在直线y=kx﹣1上,则y随x的增大而 (填“增大”或“减小”).
11.直线y=2x﹣4向右平移m个单位后的解析式为y=2x﹣10,则m= .
12.若一次函数y=(1﹣m)x+2,函数值y随x的增大而减小,则m的取值范围是 .
13.若一次函数y=(2m﹣1)x+3的图象,y随x的增大而减小,则m的取值范围是 .
14.已知点A(a,﹣2),B(b,﹣4)在直线y=﹣x+6上,则a、b的大小关系是a b.
15.如图,直线y=kx+b交x轴于点A,交y轴于点B,则不等式kx+b<0的解集为 .
16.A,B两地相距100千米,甲、乙两人骑车同时分别从A,B两地相向而行.假设他们都保持匀速行驶,则他们各自到A地的距离S(千米)都是骑车时间t(时)的一次函数.如图,直线l1、l2分别表示甲、乙骑车S与t之间关系的图象.结合图象提供的信息,经过 小时两人相遇.
17.若一次函数y=kx+b的图象经过点(1,﹣1),(2,1),则不等式kx+b>1的解集为 .
18.若一次函数图象经过点(﹣2,1),截距是3,则一次函数的解析式是 .
三.解答题(共7小题)
19.平面直角坐标系xOy内,一次函数y=2x﹣2经过点A(﹣1,m)和B(n,2).
(1)求m,n的值;
(2)求该直线与x轴的交点坐标.
20.已知一次函数y=kx+b的图象经过点A(0,2)和点B(1,3).
(1)求此一次函数的解析式;
(2)若一次函数y=kx+b的图象与x轴相交于点C,求△OBC的面积.
21.已知一次函数y=(m+1)x+2m﹣1(m≠﹣1)的图象过点(m,3).
(1)求一次函数的表达式;
(2)若A(x1,t),B(x2,t+1)是该一次函数图象上的两点,比较x1与x2的大小.
22.如图,一次函数y1=﹣2x+m与正比例函数y2=kx的图象交于点A(2,1);
(1)求出m,k的值.
(2)若y1>y2,请直接写出x的取值范围.
23.元旦期间,小黄自驾游去了离家156千米的黄石矿博园,右图是小黄离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
(1)求小黄出发0.5小时时,离家的距离;
(2)求出AB段的图象的函数解析式;
(3)小黄出发1.5小时时,离目的地还有多少千米?
24.如图,直线y=﹣x+1和直线y=x﹣2相交于点P,分别与y轴交于A、B两点.
(1)求点P的坐标;
(2)求△ABP的面积;
(3)M、N分别是直线y=﹣x+1和y=x﹣2上的两个动点,且MN∥y轴,若MN=5,直接写出M、N两点的坐标.
25.某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?最大利润是多少?
参考答案
一.选择题(共6小题)
1.下列关于x的函数中,一次函数是( )
A.y=kx+1 B.y=x+ C.y=﹣ D.y=﹣5x
解:A、y=kx+1,没有k≠0的条件,不是一次函数,不符合题意;
B、x在分母中,不是一次函数,不符合题意;
C、是反比例函数,不是一次函数,不符合题意;
D、符合一次函数的定义,是一次函数,符合题意;
故选:D.
2.函数y=5﹣2x,y的值随x值的增大而( )
A.增大 B.减小
C.不变 D.先增大后减小
解:∵y=5﹣2x,k=﹣2<0,
∴y的值随x值的增大而减小,
故选:B.
3.一次函数y=﹣3x﹣1的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
解:∵一次函数y=﹣3x﹣1,k=﹣3,b=﹣1,
∴该函数图象经过第二、三、四象限,不经过第一象限,
故选:A.
4.直线y=﹣2x+6与两坐标轴围成的三角形的面积是( )
A.8 B.6 C.9 D.2
解:在直线y=﹣2x+6中,
当x=0时,y=6;
当y=0时,x=3;
∴直线y=﹣2x+6与坐标轴交于(0,6),(3,0)两点,
∴直线y=﹣2x+6与两坐标轴围成的三角形面积=×6×3=9.
故选:C.
5.如图,直线y=﹣x+6与x轴,y轴分别交于点A和点B,点M是线段AB的中点,则线段OM的长为( )
A.4.8 B.5 C.6 D.8
解:把x=0代入y=﹣x+6得:
y=6,
即点B的坐标为(0,6),
把y=0代入y=﹣x+6得:
﹣x+6=0,
解得:x=8,
即点A的坐标为(8,0),
∴AB==10,
∵点M是线段AB的中点,
∴OM=AB=5,
故选:B.
6.若一次函数y=(1+2k)x+k﹣1的图象不经过第一象限,则k的取值范围是( )
A.k<﹣ B.﹣≤k<1且k≠0
C.﹣<k≤1 D.k≥1
解:当一次函数y=(1+2k)x+k﹣1的图象经过第二、四象限时,,无解,舍去;
当一次函数y=(1+2k)x+k﹣1的图象经过第二、三、四象限时,,
解得:k<﹣.
故选:A.
二.填空题(共12小题)
7.已知一次函数y=(m﹣1)x|m|﹣2,则m= ﹣1 .
解:∵y=(m﹣1)x|m|﹣2是一次函数,
∴|m|=1,m﹣1≠0,
解得m=﹣1.
故答案为:﹣1.
8.已知一次函数y=kx+1的图象经过点P(﹣1,0),则k= 1 .
解:∵一次函数y=kx+1的图象经过点P(﹣1,0),
∴0=﹣k+1
∴k=1
故答案为:1
9.直线y=kx+b与直线y=3x﹣1平行,则k的值是 3 .
解:∵直线y=kx+b与直线y=3x﹣1平行,
∴k=3,
故答案为3.
10.已知点(2,1)在直线y=kx﹣1上,则y随x的增大而 增大 (填“增大”或“减小”).
解:∵点(2,1)在直线y=kx﹣1上,
∴1=2k﹣1,
∴k=1.
又∵k=1>0,
∴y随x的增大而增大.
故答案为:增大.
11.直线y=2x﹣4向右平移m个单位后的解析式为y=2x﹣10,则m= 3 .
解:∵直线y=2x﹣4向右平移m个单位后的解析式为y=2x﹣10,
∴y=2(x﹣m)﹣4=2x﹣10,
则﹣2m﹣4=﹣10,
解得:m=3.
故答案为:3.
12.若一次函数y=(1﹣m)x+2,函数值y随x的增大而减小,则m的取值范围是 m>1 .
解:∵一次函数y=(1﹣m)x+2,y随x的增大而减小,
∴1﹣m<0,
解得,m>1.
故答案是:m>1.
13.若一次函数y=(2m﹣1)x+3的图象,y随x的增大而减小,则m的取值范围是 .
解:∵函数值y随自变量x的增大而减小,
∴2m﹣1<0,
∴m<.
故答案为m.
14.已知点A(a,﹣2),B(b,﹣4)在直线y=﹣x+6上,则a、b的大小关系是a < b.
解:因为﹣1<0,一次函数y随x的增大而减小,
又﹣2>﹣4,
所以,a<b.
15.如图,直线y=kx+b交x轴于点A,交y轴于点B,则不等式kx+b<0的解集为 x<﹣3 .
解:∵直线y=kx+b交x轴于A(﹣3,0),
∴点A左边的部分的x的值满足不等式kx+b<0,
∴不等式kx+b<0的解集是x<﹣3.
故答案为:x<﹣3.
16.A,B两地相距100千米,甲、乙两人骑车同时分别从A,B两地相向而行.假设他们都保持匀速行驶,则他们各自到A地的距离S(千米)都是骑车时间t(时)的一次函数.如图,直线l1、l2分别表示甲、乙骑车S与t之间关系的图象.结合图象提供的信息,经过 小时两人相遇.
解:设l1的关系式为:s1=kt,则30=k×2,解得:k=15,故s1=15t;
设s2=at+b,将(0,100),(2,60),
则,
解得:,
故l2的关系式为s2=﹣20t+100;
15t=﹣20t+100,
t=.
即他们经过小时两人相遇.
故答案为:
17.若一次函数y=kx+b的图象经过点(1,﹣1),(2,1),则不等式kx+b>1的解集为 x>2 .
解:如图所示:不等式kx+b>1的解为:x>2.
故答案为x>2.
18.若一次函数图象经过点(﹣2,1),截距是3,则一次函数的解析式是 y=x+3 .
解:截距为3,说明b=3,那么可设所求的函数解析式为y=kx+3,经过点(﹣2,1),
代入函数解析式得:﹣2k+3=1,解得k=1.
∴一次函数的解析式是y=x+3.
三.解答题(共7小题)
19.平面直角坐标系xOy内,一次函数y=2x﹣2经过点A(﹣1,m)和B(n,2).
(1)求m,n的值;
(2)求该直线与x轴的交点坐标.
解:(1)当x=﹣1时,y=2×(﹣1)﹣2=﹣4,
∴m=﹣4;
当y=2时,2x﹣2=2,解得:x=2,
∴n=2.
(2)当y=0时,2x﹣2=0,解得:x=1,
∴该直线与x轴的交点坐标为(1,0).
20.已知一次函数y=kx+b的图象经过点A(0,2)和点B(1,3).
(1)求此一次函数的解析式;
(2)若一次函数y=kx+b的图象与x轴相交于点C,求△OBC的面积.
解:(1)∵一次函数y=kx+b的图象经过点A(0,2)和点B(1,3),
∴,
解得:,
∴一次函数解析式为y=x+2;
(2)∵当y=0时,x+2=0,
解得x=﹣2,
∴与x轴相交于点C坐标为(﹣2,0),
∴S△OBC=2×3=3.
21.已知一次函数y=(m+1)x+2m﹣1(m≠﹣1)的图象过点(m,3).
(1)求一次函数的表达式;
(2)若A(x1,t),B(x2,t+1)是该一次函数图象上的两点,比较x1与x2的大小.
解:(1)∵一次函数y=(m+1)x+2m﹣1(m≠﹣1)的图象过点(m,3).
∴3=(m+1)m+2m﹣1,
解得m1=1,m2=﹣4,
∴一次函数的表达式为y=2x+1或y=﹣3x﹣9;
(2)若A(x1,t),B(x2,t+1)是一次函数y=2x+1图象上的两点,
∵k=2>0,
∴y随x的增大而增大,
∵t<t+1,
∴x1<x2;
若A(x1,t),B(x2,t+1)是一次函数y=﹣3x﹣9图象上的两点,
∵k=﹣3<0,
∴y随x的增大而减小,
∵t<t+1,
∴x1>x2.
22.如图,一次函数y1=﹣2x+m与正比例函数y2=kx的图象交于点A(2,1);
(1)求出m,k的值.
(2)若y1>y2,请直接写出x的取值范围.
解:(1)∵一次函数y1=﹣2x+m与正比例函数y2=kx的图象交于点A(2,1),
∴把A的坐标代入函数解析式得:1=﹣4+m,1=2k,
解得:m=5,k=;
(2)由图象可知,若y1>y2,则x的取值范围是x<2.
23.元旦期间,小黄自驾游去了离家156千米的黄石矿博园,右图是小黄离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
(1)求小黄出发0.5小时时,离家的距离;
(2)求出AB段的图象的函数解析式;
(3)小黄出发1.5小时时,离目的地还有多少千米?
解:(1)设OA段图象的函数表达式为y=kx.
∵当x=0.8时,y=48,
∴0.8k=48,
∴k=60.
∴y=60x(0≤x≤0.8),
∴当x=0.5时,y=60×0.5=30.
故小黄出发0.5小时时,离家30千米;
(2)设AB段图象的函数表达式为y=k′x+b.
∵A(0.8,48),B(2,156)在AB上,
,
解得,
∴y=90x﹣24(0.8≤x≤2);
(3)∵当x=1.5时,y=90×1.5﹣24=111,
∴156﹣111=45.
故小黄出发1.5小时时,离目的地还有45千米.
24.如图,直线y=﹣x+1和直线y=x﹣2相交于点P,分别与y轴交于A、B两点.
(1)求点P的坐标;
(2)求△ABP的面积;
(3)M、N分别是直线y=﹣x+1和y=x﹣2上的两个动点,且MN∥y轴,若MN=5,直接写出M、N两点的坐标.
解:(1)∵直线y=﹣x+1和直线y=x﹣2相交于点P
∴,
解之得:,
∴P点坐标为:,
(2)∵直线y=﹣x+1和直线y=x﹣2分别交y轴于A、B两点
∴A(0,1),B(0,﹣2),
∴AB=3,
由(1)知P
∴S△ABP==;
(3)设M(m,﹣m+1),则N(m,m﹣2),
∵MN=5,
∴|﹣m+1﹣(m﹣2)|=5,
解得m=﹣1或m=4,
∴M(4,﹣3),N(4,2)或M(﹣1,2),N(﹣1,﹣3).
25.某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?最大利润是多少?
解:(1)设每台A型电脑销售利润为a元,每台B型电脑的销售利润为b元;
根据题意得,
解得.
答:每台A型电脑销售利润为100元,每台B型电脑的销售利润为150元;
(2)①根据题意得,y=100x+150(100﹣x),
即y=﹣50x+15000;
②据题意得,100﹣x≤2x,
解得x≥33,
∵y=﹣50x+15000,
∴y随x的增大而减小,
∵x为正整数,
∴当x=34时,y取最大值,则100﹣x=66,
此时最大利润是y=﹣50×34+15000=13300.
即商店购进34台A型电脑和66台B型电脑的销售利润最大,最大利润是13300元.
