北师大版八年级下册1.4.1角平分线的性质与判定课件 (共27张PPT)
文档属性
| 名称 | 北师大版八年级下册1.4.1角平分线的性质与判定课件 (共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 741.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 00:00:00 | ||
图片预览





文档简介
1.4 角平分线
第1课时 角平分线的性质与判定
学习目标
一、角平分线的性质.
二、角平分线的判定定理.
复习旧知
1.线段垂直平分线的性质?
2.线段垂直平分线的判定定理?
线段垂直平分线上的点到线段两个端点的距离相等。
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
情境导入
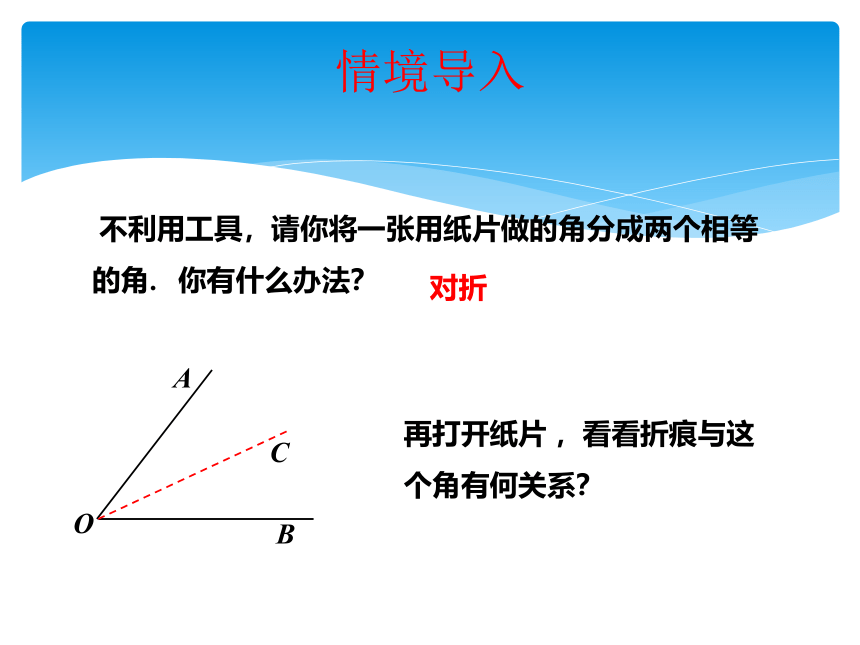
不利用工具,请你将一张用纸片做的角分成两个相等
的角. 你有什么办法?
A
O
B
C
再打开纸片 ,看看折痕与这个角有何关系?
对折
角平分线的性质
还记得角平分线上的点有什么性质吗?你是怎样得到的?请你尝试证明这性质,并与同伴交流.
感知新知一
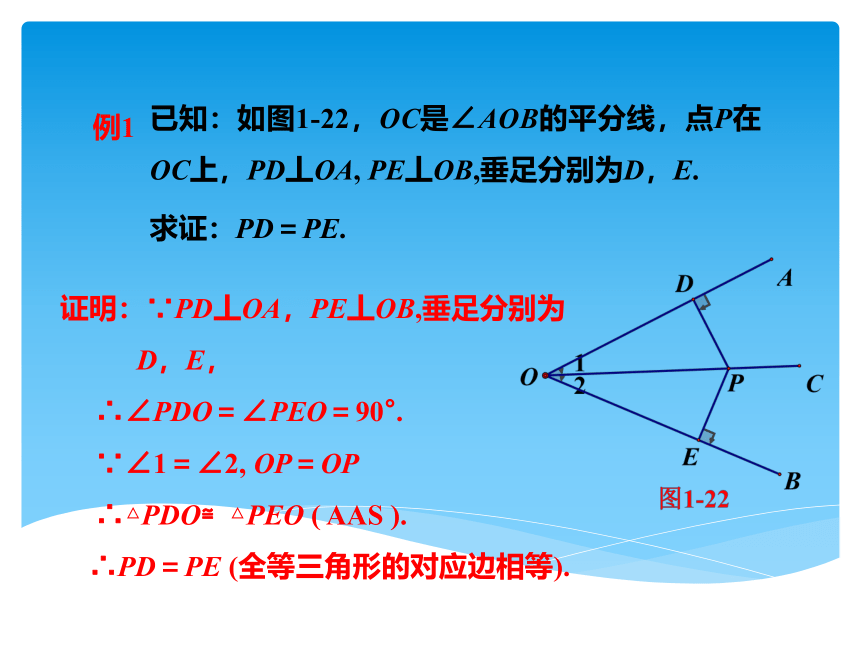
已知:如图1-22,OC是∠AOB的平分线,点P在OC上,PD丄OA, PE丄OB,垂足分别为D,E.
求证:PD=PE.
例1
证明:∵PD丄OA,PE丄OB,垂足分别为D,E,
∴∠PDO=∠PEO=90°.
∵∠1=∠2, OP=OP
∴△PDO≌△PEO ( AAS ).
∴PD=PE (全等三角形的对应边相等).
归 纳
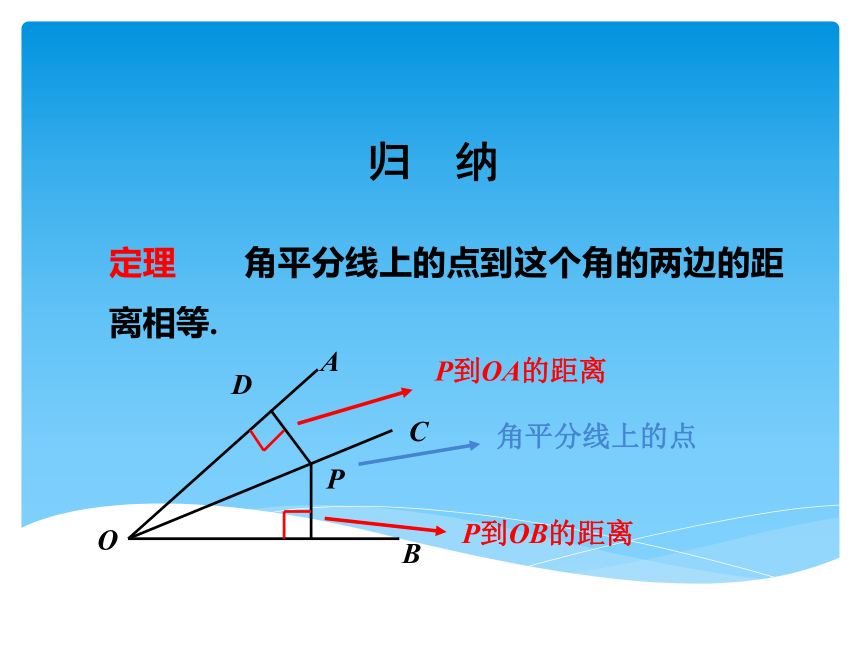
定理 角平分线上的点到这个角的两边的距离相等.
O
D
P
P到OA的距离
P到OB的距离
角平分线上的点
A
C
B
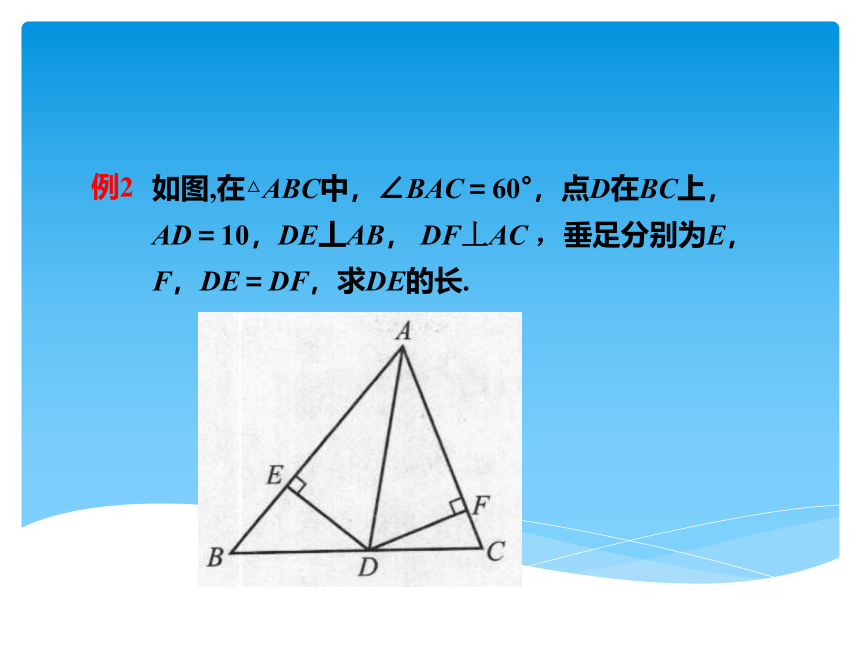
例2
如图,在△ABC中,∠BAC=60°,点D在BC上, AD=10,DE丄AB, DF丄AC ,垂足分别为E,F,DE=DF,求DE的长.
解:
∵DE丄AB, DF丄AC,垂足分分别为E,F,
且DE=DF,
∴AD平分∠BAC (在一个角的内部,到角的两边
距离相等的点在这个角的平分线上).
又∵∠BAC=60°,
∴∠BAD=30°.
在 Rt△ADE中,∠AED=90°,AD=10,
∴DE= AD= ×10=5 (在直角三角形中,如果
一个锐角等于30°. 那么它所对的直角边等于斜
边的一半).
1.如图,AD,AE分别是△ABC中∠A的内角平分线和外角平分线,它们有什么关系?
解:AD⊥AE.
沙场练兵
2.如图,OP是∠AOB的平分线,点C,D分别在角的两边OA,OB上,添加下列条件,不能判定△POC≌△POD的选项是( )
A.PC⊥OA,PD⊥OB
B.OC=OD
C.∠OPC=∠OPD
D.PC=PD
D
3.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足
分别为A,B.下列结论中不一定成立的是( )
A.PA=PB
B.PO平分∠APB
C.OA=OB
D.AB垂直平分OP
D
4.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,若AB=69cm,则△DBE的周长是( )
A.6 cm
B.7 cm
C.8 cm
D.9 cm
D
5.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=16,则点P到BC的距离是( )
A.8
B.6
C.4
D.2
A
6.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于
MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=6,AB=15,则△ABD的面积是( )
A.15 B.30
C.45 D.60
C
如图,由 于点 D ,
于点E,PD= PE , 可
以得到什么结论 ?
OB
PE
^
PD
^
OA
B
A
D
O
P
E
到一个角的两边的距离相等
的点, 在这个角的平分线上.
探究新知二
证明过程:
已知:如图,点P为∠AOB内一点,PD丄OA,PE丄OB,垂足分别为D,E,且PD=PE.
求证:OP平分∠AOB.
证明:∵PD丄OA, PE丄OB,垂足分别为D,E,?
∴∠ODP=∠OEP=90°,
∵PD=PE,OP=OP,
∴Rt△DOP≌ Rt△EOP ( HL ).
∴∠1=∠2 (全等三角形的对应角相等).
∴OP平分∠AOB.
判定方法:角的内部到角的两边的距离相等的点在角
的平分线上.
书写格式:如图,∵PD⊥OA,PE⊥OB,PD=PE,
∴点P在∠AOB的平分线上(或∠AOC=∠BOC).
如图,已知BE=CF,DF⊥AC于点F,DE⊥AB于点E,BF和CE相交于点D.
求证:AD平分∠BAC.
例3
导引:
要证AD平分∠BAC,已知条件
中有两个垂直,即有点到角的
两边的距离,再证这两个距离
相等即可证明结论,证这两条
垂线段相等,可通过证明
△BDE和△CDF全等来完成.
∵DF⊥AC于点F,DE⊥AB于点E,
∴∠DEB=∠DFC=90°.
在△BDE和△CDF中,
∴△BDE≌△CDF(AAS).
∴DE=DF.
又∵DF⊥AC于点F,DE⊥AB于点E,
∴AD平分∠BAC.
证明:
1.如图,一目标在A区,到公路、铁路距离相等,离公路与铁路交叉处500 m,在图上标出它的位置(比例尺1:20 000).
如图,设公路、铁路的交点为O. 在A区内作角的平分线OB,在OB上截取OC=2.5 cm,则点C即为所求.
解:
亮剑迎战
2.如图,在CD上求一点P,使它到边OA,OB的距离相等,则点P是( )
A.线段CD的中点
B.CD与过点O作CD的垂线的交点
C.CD与∠AOB的平分线的交点
D.以上均不对
C
3.如图,AD⊥OB,BC⊥OA,垂足分别为D,C,AD与BC相交于点P,若PA=PB,则∠1与∠2的大小关系是( )
A.∠1=∠2
B.∠1>∠2
C.∠1<∠2
D.无法确定
A
4.如图,在△ABC中,与∠ABC,∠ACB相邻的外角的平分线相交于点F,连接AF,则下列结论正确的是( )
A.AF平分BC
B.AF平分∠BAC
C.AF⊥BC
D.以上结论都正确
B
5.如图,在△ABC中,AB=AC,D为BC上一点,连接AD,E为AD上一点,EM⊥AB于点M,EN⊥AC于点N,则下面四个结论:①若AD⊥BC,则EM=EN;②若EM=EN,则∠BAD=∠CAD;③若EM=EN,则AM=AN;④若EM=EN,则∠AEM=
∠AEN.其中正确的有( )
A.1个 B.2个
C.3个 D.4个
D
6.如图,在△ABC中,BD平分∠ABC,交AC于点D,BC边上有一点E,连接DE,则AD与DE的数量关系为( )
A.AD>DE
B.AD=DE
C.ADD.不确定
易错点:运用角的平分线的性质时,常因忽略“到角两边的距离”而导致错误
D
今天你学到了吗?
1.性质:角平分线上的点到这个角的两边的距离相等.
2.判定:在一个角的内部,到角的两边距离相等的点在这个角的平分线上.
第1课时 角平分线的性质与判定
学习目标
一、角平分线的性质.
二、角平分线的判定定理.
复习旧知
1.线段垂直平分线的性质?
2.线段垂直平分线的判定定理?
线段垂直平分线上的点到线段两个端点的距离相等。
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
情境导入
不利用工具,请你将一张用纸片做的角分成两个相等
的角. 你有什么办法?
A
O
B
C
再打开纸片 ,看看折痕与这个角有何关系?
对折
角平分线的性质
还记得角平分线上的点有什么性质吗?你是怎样得到的?请你尝试证明这性质,并与同伴交流.
感知新知一
已知:如图1-22,OC是∠AOB的平分线,点P在OC上,PD丄OA, PE丄OB,垂足分别为D,E.
求证:PD=PE.
例1
证明:∵PD丄OA,PE丄OB,垂足分别为D,E,
∴∠PDO=∠PEO=90°.
∵∠1=∠2, OP=OP
∴△PDO≌△PEO ( AAS ).
∴PD=PE (全等三角形的对应边相等).
归 纳
定理 角平分线上的点到这个角的两边的距离相等.
O
D
P
P到OA的距离
P到OB的距离
角平分线上的点
A
C
B
例2
如图,在△ABC中,∠BAC=60°,点D在BC上, AD=10,DE丄AB, DF丄AC ,垂足分别为E,F,DE=DF,求DE的长.
解:
∵DE丄AB, DF丄AC,垂足分分别为E,F,
且DE=DF,
∴AD平分∠BAC (在一个角的内部,到角的两边
距离相等的点在这个角的平分线上).
又∵∠BAC=60°,
∴∠BAD=30°.
在 Rt△ADE中,∠AED=90°,AD=10,
∴DE= AD= ×10=5 (在直角三角形中,如果
一个锐角等于30°. 那么它所对的直角边等于斜
边的一半).
1.如图,AD,AE分别是△ABC中∠A的内角平分线和外角平分线,它们有什么关系?
解:AD⊥AE.
沙场练兵
2.如图,OP是∠AOB的平分线,点C,D分别在角的两边OA,OB上,添加下列条件,不能判定△POC≌△POD的选项是( )
A.PC⊥OA,PD⊥OB
B.OC=OD
C.∠OPC=∠OPD
D.PC=PD
D
3.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足
分别为A,B.下列结论中不一定成立的是( )
A.PA=PB
B.PO平分∠APB
C.OA=OB
D.AB垂直平分OP
D
4.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,若AB=69cm,则△DBE的周长是( )
A.6 cm
B.7 cm
C.8 cm
D.9 cm
D
5.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=16,则点P到BC的距离是( )
A.8
B.6
C.4
D.2
A
6.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于
MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=6,AB=15,则△ABD的面积是( )
A.15 B.30
C.45 D.60
C
如图,由 于点 D ,
于点E,PD= PE , 可
以得到什么结论 ?
OB
PE
^
PD
^
OA
B
A
D
O
P
E
到一个角的两边的距离相等
的点, 在这个角的平分线上.
探究新知二
证明过程:
已知:如图,点P为∠AOB内一点,PD丄OA,PE丄OB,垂足分别为D,E,且PD=PE.
求证:OP平分∠AOB.
证明:∵PD丄OA, PE丄OB,垂足分别为D,E,?
∴∠ODP=∠OEP=90°,
∵PD=PE,OP=OP,
∴Rt△DOP≌ Rt△EOP ( HL ).
∴∠1=∠2 (全等三角形的对应角相等).
∴OP平分∠AOB.
判定方法:角的内部到角的两边的距离相等的点在角
的平分线上.
书写格式:如图,∵PD⊥OA,PE⊥OB,PD=PE,
∴点P在∠AOB的平分线上(或∠AOC=∠BOC).
如图,已知BE=CF,DF⊥AC于点F,DE⊥AB于点E,BF和CE相交于点D.
求证:AD平分∠BAC.
例3
导引:
要证AD平分∠BAC,已知条件
中有两个垂直,即有点到角的
两边的距离,再证这两个距离
相等即可证明结论,证这两条
垂线段相等,可通过证明
△BDE和△CDF全等来完成.
∵DF⊥AC于点F,DE⊥AB于点E,
∴∠DEB=∠DFC=90°.
在△BDE和△CDF中,
∴△BDE≌△CDF(AAS).
∴DE=DF.
又∵DF⊥AC于点F,DE⊥AB于点E,
∴AD平分∠BAC.
证明:
1.如图,一目标在A区,到公路、铁路距离相等,离公路与铁路交叉处500 m,在图上标出它的位置(比例尺1:20 000).
如图,设公路、铁路的交点为O. 在A区内作角的平分线OB,在OB上截取OC=2.5 cm,则点C即为所求.
解:
亮剑迎战
2.如图,在CD上求一点P,使它到边OA,OB的距离相等,则点P是( )
A.线段CD的中点
B.CD与过点O作CD的垂线的交点
C.CD与∠AOB的平分线的交点
D.以上均不对
C
3.如图,AD⊥OB,BC⊥OA,垂足分别为D,C,AD与BC相交于点P,若PA=PB,则∠1与∠2的大小关系是( )
A.∠1=∠2
B.∠1>∠2
C.∠1<∠2
D.无法确定
A
4.如图,在△ABC中,与∠ABC,∠ACB相邻的外角的平分线相交于点F,连接AF,则下列结论正确的是( )
A.AF平分BC
B.AF平分∠BAC
C.AF⊥BC
D.以上结论都正确
B
5.如图,在△ABC中,AB=AC,D为BC上一点,连接AD,E为AD上一点,EM⊥AB于点M,EN⊥AC于点N,则下面四个结论:①若AD⊥BC,则EM=EN;②若EM=EN,则∠BAD=∠CAD;③若EM=EN,则AM=AN;④若EM=EN,则∠AEM=
∠AEN.其中正确的有( )
A.1个 B.2个
C.3个 D.4个
D
6.如图,在△ABC中,BD平分∠ABC,交AC于点D,BC边上有一点E,连接DE,则AD与DE的数量关系为( )
A.AD>DE
B.AD=DE
C.AD
易错点:运用角的平分线的性质时,常因忽略“到角两边的距离”而导致错误
D
今天你学到了吗?
1.性质:角平分线上的点到这个角的两边的距离相等.
2.判定:在一个角的内部,到角的两边距离相等的点在这个角的平分线上.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
