北师大版八年级下册2.1 不等关系 课件(共27张PPT)
文档属性
| 名称 | 北师大版八年级下册2.1 不等关系 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 337.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 00:00:00 | ||
图片预览








文档简介
第二章 一元一次不等式与一元一次不等式组
2.1 不等关系
学习目标
一、不等式的定义
二、用不等式表示数量关系
你还记得小孩玩的翘翘板吗?你想过它的工作原理吗?其实,翘翘板就是靠不断改变两端的重量对比来工作的.
情境引入
在古代,我们的祖先就懂得了翘翘板的工作原理,并且根据这一原理设计出了一些简单机械,
并把它们用到了生活实践当中.
如下图,用两根长度均为 Lcm 的绳子,分别围成一个正方形和圆。
自主预习
1.如果要使正方形的面积不大于25cm2,那么绳长L应满足怎样的关系式?
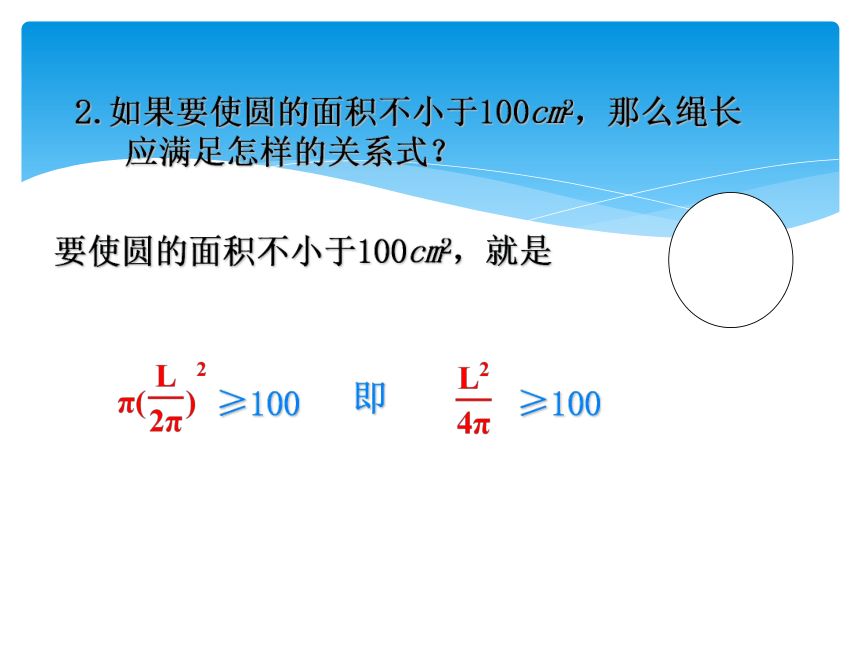
2.如果要使圆的面积不小于100cm2,那么绳长
L应满足怎样的关系式?
3.当 L = 8 时,正方形和圆的面积哪个大?
? = 12 呢?
4.你能得到什么猜想?改变L的取值再试一试。
1.如果要使正方形的面积不大于25cm2,那么绳长L应满足怎样的关系式?
在上面的问题中,所围成的正方形的面积可
以表示为 ,
要使正方形的面积不大于25cm2,就是
≤ 25
即
≤ 25
新知探究
≤ 25
要使正方形的面积不大于25cm2,就是
≤ 25
≥100
即
≥100
2.如果要使圆的面积不小于100cm2,那么绳长
应满足怎样的关系式?
要使圆的面积不小于100cm2,就是
3.当 L=8 时,正方形和圆的面积哪个大?
L= 12 呢?
当? = 8 时,
正方形的面积为:
= 4(cm)2
圆的面积为:
≈5.1(cm)2
∵4< 5.1
∴此时的圆的面积大。
3.当 L=8 时,正方形和圆的面积哪个大?
L= 12 呢?
L=12时,
正方形的面积为:
= 9(cm)2
圆的面积为:
∵9< 11.5
≈11.5(cm)2
∴此时还是圆的面积大。
在上面的问题中,所围成的都是都是圆的面积大。
4.你能得到什么猜想?改变L的取值再试一试。
我们可以猜想,用长度均为Lcm的两根绳子分别围成一个正方形和圆,无论L取何值,圆的面积总大于正方形的面积,
即
>
做一做
1.铁路部门对旅客随身携带的行李有如下规定:
每件行李的长、宽、高之和不得超过160cm。
设行李的长、宽、高分别为a cm、b cm、c cm,
请你列出行李的长、宽、高满足的关系式。
a+b+c≤160
做一做
6+3x>30
2.通过测量一棵树的树围(树干的周长)可以计算出它的树龄,通常规定以树干离地面1.5cm的地
方作为测量部位. 某树栽种时的树围为6cm, 以后10年内每年增加约3cm。设经过x年后这棵树的树围超过 30cm,请你列出x满足的关系式。
观察由上述问题得到的如下关系式,
(1)
(2)
(3)
(4)
一般地,用符号“<”(或“≤”),“>”(或“≥”)连接的式子叫做不等式。
≤ 25
≥100
>
6+3x>30
(5)a+b+c≤160
议一议
它们有什么共同特点?
判断一个式子是否为不等式的关键是看式子中是
否含有“≠”“>”“<”“≥”“≤”;因此
②③⑤⑥⑧是不等式.
导引:
下列式子是不等式的>有( )
①2x=20;②3>2;③x≠4-3;④5a+6b;
A.2个 B.3个 C.4个 D.5个
例1
D
总 结
一个式子是不等式,要把握两点:
一是含有不等号,
二是表示不等关系,而与不等式是否成立无关.
(1)a2表示非负数,∴a2≥0.
(2)|x|≥0,|y|≥0,∴|x|+|y|≥|x+y|.
(3)不小于就是大于或等于.
(4)当a是负数或0时,|a|=-a.
导引:
用不等号填空.
(1)a2____0;(2)|x|+|y|____|x+y|;
(3)若a不小于1,则a____1;
(4)当a____0时,|a|=-a.
例2
≥
≥
≥
≤
1. 用“<”或“>”号填空.
(1)-2____2; (2)-3____-2;
(3)12____6; (4)0____-8;
(5)-a____a (a>0); (6)-a____a(a<0).
2. 下列数学表达式:
①-2<0;②4x+2y>0;③x=1;④x2-xy;
⑤x≠3;⑥x-1<y+2.其中不等式有( )
A.5个 B.4个 C.3个 D.2个
<
<
>
>
<
>
B
牛刀小试
用不等式表示数量关系
1. 列不等式就是用不等式表示代数式之间的不等关系.
2. 列不等式的一般步骤:
(1)分析题意,找出问题中的各种量;
(2)弄清各种量之间的数量关系;
(3)用代数式表示各种量;
(4)用适当的不等号将具有不等关系的量连接起来.
(1)中“正数”用“>0”表示;
(3)中“非正数”即负数或0,用“≤0”表示;
(4)中“不大于”即“小于或等于”,用“≤”表
示.
例3
导引:
列不等式:
(1)a与1的和是正数:________;
(2)y的2倍与1的和大于3:________;
(3)x的一半与x的2倍的和是非正数:__________;
(4)c与4的和不大于-2:________.
a+1>0
2y+1>3
c+4≤-2
列不等式首先要找出表示不等关系的关键词,然后用
表示数量关系的式子表示不等式的左边和右边;
常用不等关系的基本语言的意义:
(1)a是正数等价于a>0; (2)a是负数等价于a<0;
(3)a是非正数等价于a≤0; (4)a是非负数等价于a≥0;
(5)a大于b等价于a-b>0; (6)a小于b等价于a-b<0;
(7)a不大于b等价于a≤b; (8)a不小于b等价于a≥b;
(9)a,b同号等价于ab>0或 >0;
(10)a,b异号等价于ab<0或 <0.,
总 结
1.用适当的符号表示下列关系:
(1)a是非负数;
(2)直角三角形斜边c比它的两直角边a,b都长;
(3)x与17的和比它的5倍小;
(4)两数的平方和不小于这两数积的2倍.
解:(1)a≥0. (2)c>a,c>b.
(3)x+17<5x. (4)x2+y2≥2xy.
华山论剑,初试锋芒
2.用不等式表示“x的2倍与5的差是负数”正确
的是( )
A.2x-5>0 B.2x-5<0
C.2x-5≠0 D.2x-5≤0
B
3.如图,A,B两点在数轴上表示的数
分别为a,b,下列式子成立的是( )
A.ab>0 B.a+b<0
C.(b-1)(a+1)>0 D.(b-1)(a-1)>0
C
4.如图,每个小正方形的边长为1,△ABC的
三边a,b,c的大小关系是( )
A.a<c<b
B.a<b<c
C.c<a<b
D.c<b<a
C
5. 某市的最高气温是33 ℃,最低气温是24 ℃,则该市的气温t(℃)的变化范围是( )
A.t>33 B.t≤24
C.24<t<33 D.24≤t≤33
D
这节课的学习,你有哪些收获?
1.不等式:一般地,用符号“<”(或“≤”),“>”(或“≥”)连接的式子叫做不等式。
2. 列不等式是用不等式表示代数式之间的不等关系.
3. 列不等式的一般步骤:
(1)分析题意,找出问题中的各种量;
(2)弄清各种量之间的数量关系;
(3)用代数式表示各种量;
(4)用适当的不等号将具有不等关系的量连接起来.
2.1 不等关系
学习目标
一、不等式的定义
二、用不等式表示数量关系
你还记得小孩玩的翘翘板吗?你想过它的工作原理吗?其实,翘翘板就是靠不断改变两端的重量对比来工作的.
情境引入
在古代,我们的祖先就懂得了翘翘板的工作原理,并且根据这一原理设计出了一些简单机械,
并把它们用到了生活实践当中.
如下图,用两根长度均为 Lcm 的绳子,分别围成一个正方形和圆。
自主预习
1.如果要使正方形的面积不大于25cm2,那么绳长L应满足怎样的关系式?
2.如果要使圆的面积不小于100cm2,那么绳长
L应满足怎样的关系式?
3.当 L = 8 时,正方形和圆的面积哪个大?
? = 12 呢?
4.你能得到什么猜想?改变L的取值再试一试。
1.如果要使正方形的面积不大于25cm2,那么绳长L应满足怎样的关系式?
在上面的问题中,所围成的正方形的面积可
以表示为 ,
要使正方形的面积不大于25cm2,就是
≤ 25
即
≤ 25
新知探究
≤ 25
要使正方形的面积不大于25cm2,就是
≤ 25
≥100
即
≥100
2.如果要使圆的面积不小于100cm2,那么绳长
应满足怎样的关系式?
要使圆的面积不小于100cm2,就是
3.当 L=8 时,正方形和圆的面积哪个大?
L= 12 呢?
当? = 8 时,
正方形的面积为:
= 4(cm)2
圆的面积为:
≈5.1(cm)2
∵4< 5.1
∴此时的圆的面积大。
3.当 L=8 时,正方形和圆的面积哪个大?
L= 12 呢?
L=12时,
正方形的面积为:
= 9(cm)2
圆的面积为:
∵9< 11.5
≈11.5(cm)2
∴此时还是圆的面积大。
在上面的问题中,所围成的都是都是圆的面积大。
4.你能得到什么猜想?改变L的取值再试一试。
我们可以猜想,用长度均为Lcm的两根绳子分别围成一个正方形和圆,无论L取何值,圆的面积总大于正方形的面积,
即
>
做一做
1.铁路部门对旅客随身携带的行李有如下规定:
每件行李的长、宽、高之和不得超过160cm。
设行李的长、宽、高分别为a cm、b cm、c cm,
请你列出行李的长、宽、高满足的关系式。
a+b+c≤160
做一做
6+3x>30
2.通过测量一棵树的树围(树干的周长)可以计算出它的树龄,通常规定以树干离地面1.5cm的地
方作为测量部位. 某树栽种时的树围为6cm, 以后10年内每年增加约3cm。设经过x年后这棵树的树围超过 30cm,请你列出x满足的关系式。
观察由上述问题得到的如下关系式,
(1)
(2)
(3)
(4)
一般地,用符号“<”(或“≤”),“>”(或“≥”)连接的式子叫做不等式。
≤ 25
≥100
>
6+3x>30
(5)a+b+c≤160
议一议
它们有什么共同特点?
判断一个式子是否为不等式的关键是看式子中是
否含有“≠”“>”“<”“≥”“≤”;因此
②③⑤⑥⑧是不等式.
导引:
下列式子是不等式的>有( )
①2x=20;②3>2;③x≠4-3;④5a+6b;
A.2个 B.3个 C.4个 D.5个
例1
D
总 结
一个式子是不等式,要把握两点:
一是含有不等号,
二是表示不等关系,而与不等式是否成立无关.
(1)a2表示非负数,∴a2≥0.
(2)|x|≥0,|y|≥0,∴|x|+|y|≥|x+y|.
(3)不小于就是大于或等于.
(4)当a是负数或0时,|a|=-a.
导引:
用不等号填空.
(1)a2____0;(2)|x|+|y|____|x+y|;
(3)若a不小于1,则a____1;
(4)当a____0时,|a|=-a.
例2
≥
≥
≥
≤
1. 用“<”或“>”号填空.
(1)-2____2; (2)-3____-2;
(3)12____6; (4)0____-8;
(5)-a____a (a>0); (6)-a____a(a<0).
2. 下列数学表达式:
①-2<0;②4x+2y>0;③x=1;④x2-xy;
⑤x≠3;⑥x-1<y+2.其中不等式有( )
A.5个 B.4个 C.3个 D.2个
<
<
>
>
<
>
B
牛刀小试
用不等式表示数量关系
1. 列不等式就是用不等式表示代数式之间的不等关系.
2. 列不等式的一般步骤:
(1)分析题意,找出问题中的各种量;
(2)弄清各种量之间的数量关系;
(3)用代数式表示各种量;
(4)用适当的不等号将具有不等关系的量连接起来.
(1)中“正数”用“>0”表示;
(3)中“非正数”即负数或0,用“≤0”表示;
(4)中“不大于”即“小于或等于”,用“≤”表
示.
例3
导引:
列不等式:
(1)a与1的和是正数:________;
(2)y的2倍与1的和大于3:________;
(3)x的一半与x的2倍的和是非正数:__________;
(4)c与4的和不大于-2:________.
a+1>0
2y+1>3
c+4≤-2
列不等式首先要找出表示不等关系的关键词,然后用
表示数量关系的式子表示不等式的左边和右边;
常用不等关系的基本语言的意义:
(1)a是正数等价于a>0; (2)a是负数等价于a<0;
(3)a是非正数等价于a≤0; (4)a是非负数等价于a≥0;
(5)a大于b等价于a-b>0; (6)a小于b等价于a-b<0;
(7)a不大于b等价于a≤b; (8)a不小于b等价于a≥b;
(9)a,b同号等价于ab>0或 >0;
(10)a,b异号等价于ab<0或 <0.,
总 结
1.用适当的符号表示下列关系:
(1)a是非负数;
(2)直角三角形斜边c比它的两直角边a,b都长;
(3)x与17的和比它的5倍小;
(4)两数的平方和不小于这两数积的2倍.
解:(1)a≥0. (2)c>a,c>b.
(3)x+17<5x. (4)x2+y2≥2xy.
华山论剑,初试锋芒
2.用不等式表示“x的2倍与5的差是负数”正确
的是( )
A.2x-5>0 B.2x-5<0
C.2x-5≠0 D.2x-5≤0
B
3.如图,A,B两点在数轴上表示的数
分别为a,b,下列式子成立的是( )
A.ab>0 B.a+b<0
C.(b-1)(a+1)>0 D.(b-1)(a-1)>0
C
4.如图,每个小正方形的边长为1,△ABC的
三边a,b,c的大小关系是( )
A.a<c<b
B.a<b<c
C.c<a<b
D.c<b<a
C
5. 某市的最高气温是33 ℃,最低气温是24 ℃,则该市的气温t(℃)的变化范围是( )
A.t>33 B.t≤24
C.24<t<33 D.24≤t≤33
D
这节课的学习,你有哪些收获?
1.不等式:一般地,用符号“<”(或“≤”),“>”(或“≥”)连接的式子叫做不等式。
2. 列不等式是用不等式表示代数式之间的不等关系.
3. 列不等式的一般步骤:
(1)分析题意,找出问题中的各种量;
(2)弄清各种量之间的数量关系;
(3)用代数式表示各种量;
(4)用适当的不等号将具有不等关系的量连接起来.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
